3 Дисперсия, ее виды и свойства

Наряду с изучением вариации признака по всей совокупности в целом часто бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а так же между группами. Различают следующие виды дисперсии:

1) Общая дисперсия изучает вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию:

.

2) Межгрупповая дисперсия характеризует колеблемость групповых средних около общей средней и отражает различия в величине изучаемого признака, возникающие под влиянием неучтенных факторов и независящую от признака – фактора, положенного в основание группировки:

,

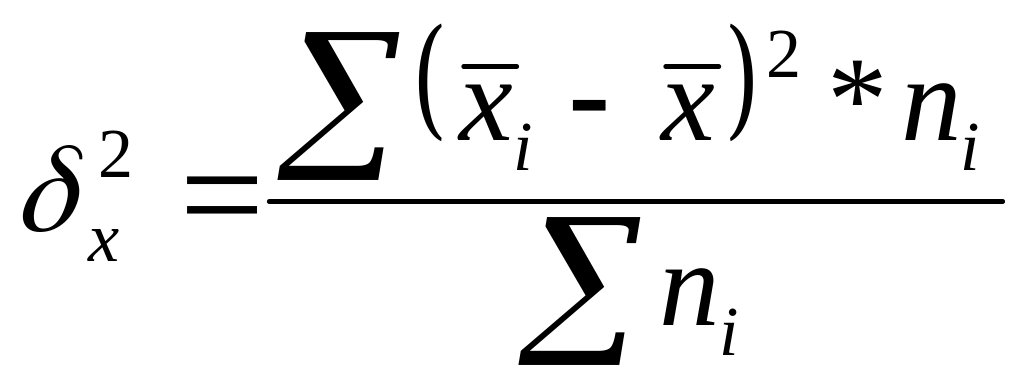где - средняя по i-ой группе,

- численность i-ой группы.

3) Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и независящую от признака – фактора, положенного в основание группировки:

.

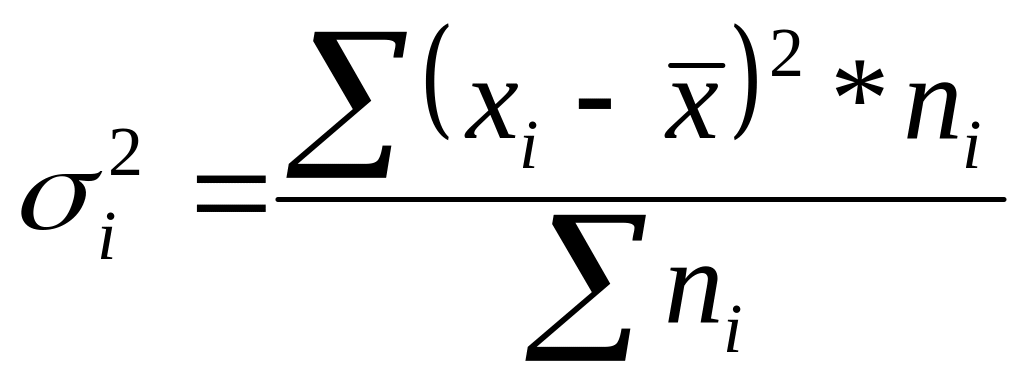Средняя из внутригрупповых дисперсий .

Существует закон сложения дисперсий: .

В статистическом анализе широко используется эмпирический коэффициент детерминации:

.

Эмпирическое корреляционное отношение характеризует влияние признака, положенного в основание группировки, на вариацию результативного признака:

,

Эмпирическое корреляционное отношение находится в пределах . Если , то группировочный признак не оказывает влияние на результативный. Если , то результативный признак зависит от группировочного признака.

Свойства дисперсии:

1) Дисперсия постоянной величины равна нулю.

2) Уменьшение всех значений признака на одну и ту же величину А не меняет величины дисперсии:

.

3) Уменьшение всех значений признака в А раз уменьшает дисперсию в А² раз:

.

4) Если исчислить средний квадрат отклонений от любой величины А, которая в той или иной степени отличается от средней арифметической , то он всегда будет > среднего квадрата отклонений, исчисленного от средней арифметической:

.

4 Характеристика закономерности рядов распределения

Одной из важных задач в статистике является выявление закономерности распределения и определение ее характера. В вариационных рядах существует определенная связь в изменении частот и значений признака: с увеличением значений признака частоты вначале возрастают до определенной величины, а затем убывают. Такие изменения частот в вариационных рядах называются закономерностями распределения.

Для получения представления о форме распределения строятся графики кривых распределения (полигоны, гистограммы).

Кривая распределения – это графическое изображение в виде непрерывной линии изменений частот в вариационном ряду, отражающая как общие, так и случайные условия, определяющие распределение.

В статистической практике встречаются различные виды распределений. Наиболее общим является распределение, называемое нормальным.

Нормальное распределение предполагает, что:

- отклонения от среднего значения являются результатом большого количества мелких отклонений;

- позитивные и негативные отклонения равновероятны;

- наиболее вероятным значением всех, в равной мере надежных измерений, является их средняя арифметическая.

Нормальное распределение описывается уравнением:

,

где - ордината кривой нормального распределения;

- нормированное отклонение;

и математические постоянные;

- варианты вариационного ряда;

- средняя величина;

- среднее квадратическое отклонение.

Согласно нормальному закону распределения колеблемость индивидуальных значений признака находится в пределах :

- 68,3%

- 95,4%

- 99,7%.

Нормальному распределению соответствует симметричное распределение, но чаще всего встречается асимметричное распределение. В нем вершина кривой сдвинута либо вправо, либо влево.

Если вершина сдвинута влево, то правая часть длиннее левой и асимметрия является правосторонней

Если вершина сдвинута вправо, то левая часть длиннее правой и асимметрия является левосторонней

Асимметрия измеряется с помощью следующих показателей:

.

Если As>0, то асимметрия правосторонняя, если As<0, то асимметрия левосторонняя.

Показатель, основанный на моменте третьего порядка:

,

где - центральный момент третьего порядка. Если , то асимметрия считается значительной, в противном случае незначительной.

Оценка существенности этого показателя дается с помощью среднеквадратической ошибки: , где n – это число наблюдений. Если , то асимметрия не существенна и обусловлена влиянием случайных факторов, в противном случае распределение признака в совокупности не является асимметричным.

Для симметричных распределений рассчитывается эксцесс.

Эксцесс – это высоковершинность (островершинность) или низковершинность (плосковершинность) фактической кривой распределения по сравнению с нормальным распределением.

Высоковершинность (островершинность) означает положительный эксцесс и характеризует скопление частот в середине ряда.

Низковершинность (плосковершинность) означает отрицательный эксцесс и характеризует большую разбросанность членов ряда.

Эксцесс определяется по формуле с использованием центрального момента четвертого порядка:

.

где 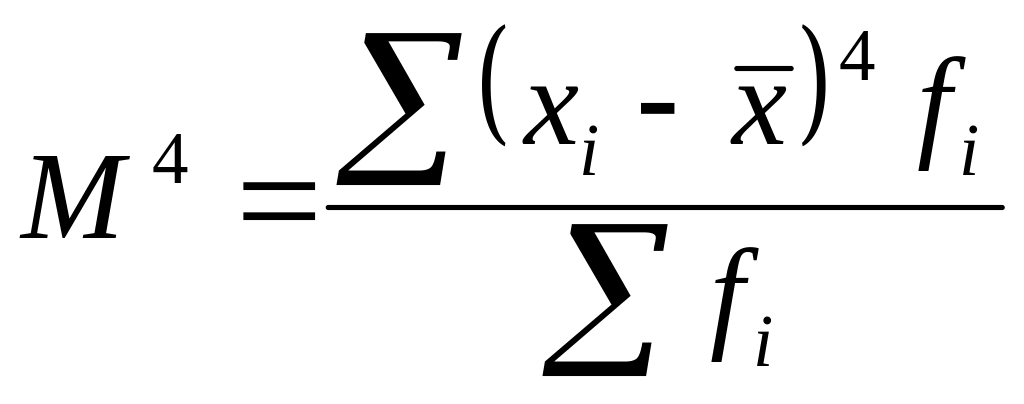- центральный момент четвертого порядка.

Оценка степени существенности показателя дается с помощью среднеквадратической ошибки эксцесса . Если , то это свидетельствует о незначительном эксцессе.

Для проверки соответствия фактического распределения нормальному производится сравнение частот фактического распределения с теоретическими частотами, которые характерны для нормального распределения. На основе этого строится теоретическая кривая.

Процесс нахождения функции кривой распределения принято называть аппроксимацией или выравниванием. Он заключается в следующем:

- подборе и теоретическом обосновании предельной теоретической кривой плотности распределения достаточно точно выражающей свойственную явлению закономерность;

- определение параметров фактической кривой распределения;

- оценка близости эмпирического и теоретического распределения при помощи математических критериев.

Рассмотрим аппроксимацию на основе функции нормального распределения выполнения норм выработки рабочими цеха:

№ цеха	Группы рабочих по выполнению норм выработки, %	Число рабочих	Центры интервалов		Значение плотности вероятности	Теоретические частоты
1	До 100	2	95	-2,03	0,0508	4
2	100 - 110	15	105	-1,30	0,1714	12
3	110 - 120	26	115	-0,58	0,3372	25
4	120 - 130	32	125	0,14	0,3951	29
5	130 - 140	12	135	0,87	0,2732	20
6	140 - 150	9	145	1,59	0,1127	8
7	150 - 160	4	155	2,32	0,0270	2
	Итого	100				100

Значение плотности вероятности для нормального закона распределения определяется по таблице “плотность нормального закона распределения” (Шмойлова, приложение 8).

Определение теоретических частот производится на основе следующего уравнения: ,

Где - теоретические частоты;

- величина интервала;

- сумма частот (объем совокупности);

.

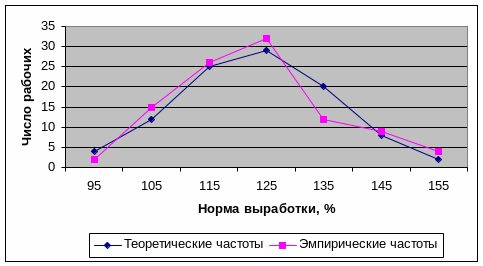
Для того, чтобы установить верно ли предположение о том, что эмпирическое распределение подчинено закону нормального распределения, необходимо сравнить его с теоретическим распределением. Чем ближе значение к нулю, тем ближе фактическое распределение к теоретическому.

Для оценки степени близости эмпирического распределения к теоретическому, используются критерии согласия.

Критерий согласия Пирсона (хи - квадрат):

где - частоты эмпирического распределения;

- частоты теоретического распределения.

Если , то это означает, что эмпирическое распределение соответствует нормальному. определяется по специальным таблицам в зависимости от принятой вероятности P и числа степеней свободы …