Задачі для самостійного розв’язування

1. Точка рухається вздовж прямої згідно з рівнянням 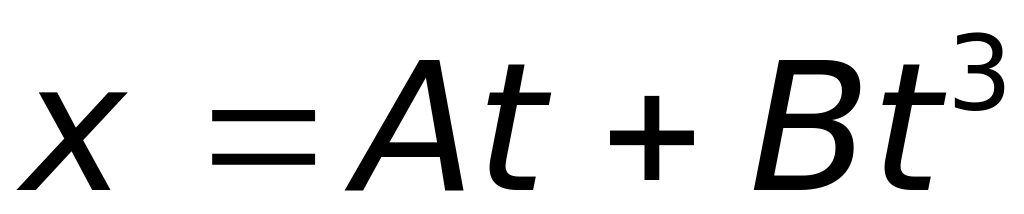, де 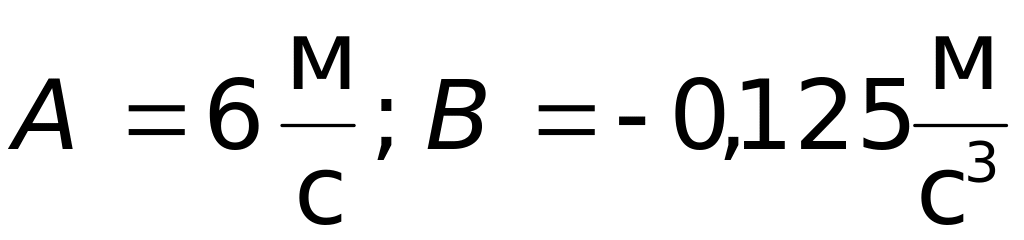. Визначити середню шляхову швидкість точки в інтервалі часу від .

Відповідь: .

2. Визначити середню шляхову швидкість тіла , якщо

   1. тіло проходить N однакових ділянок шляху із сталими у межах ділянки швидкостями

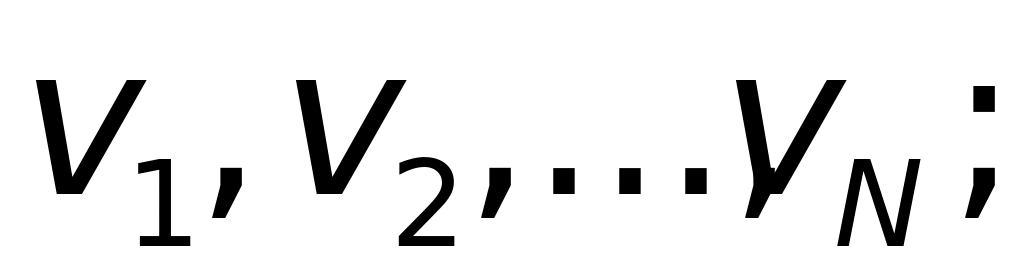
   2. тіло рухається так, що швидкості його на протязі кожного з N рівних проміжків часу .

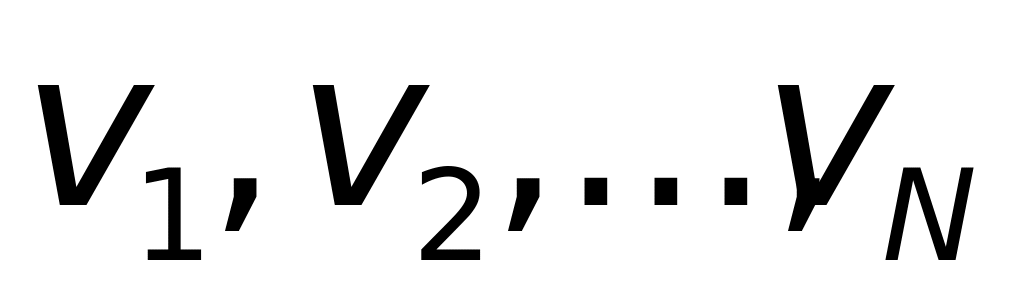Відповідь: а) 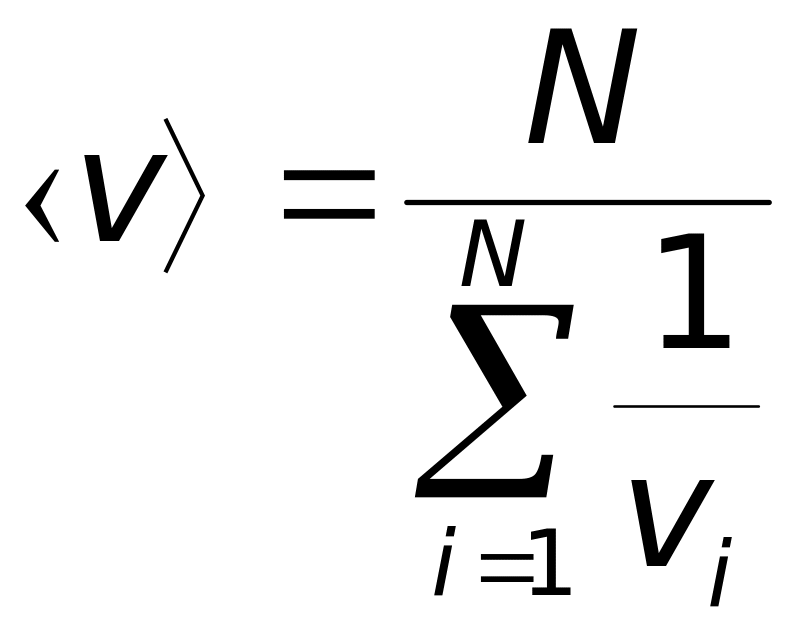; б) .

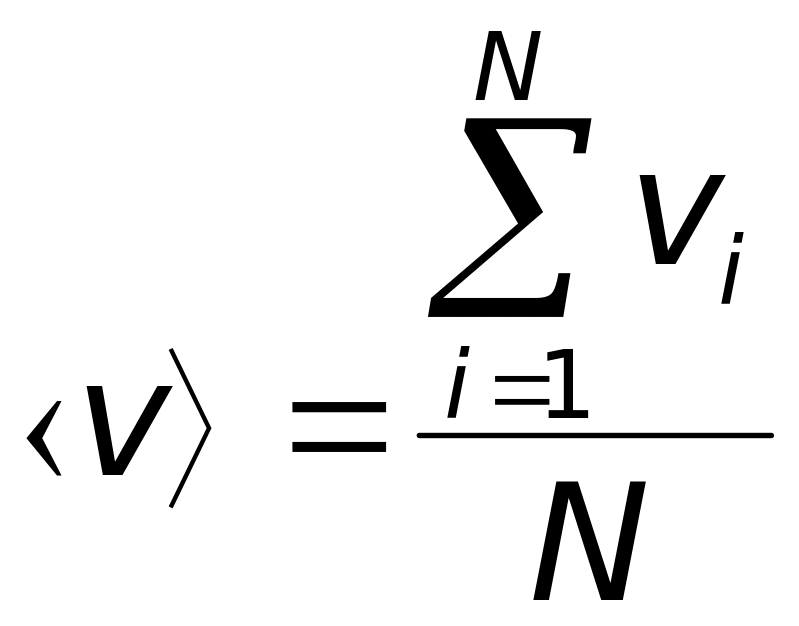Приклад 6

За проміжок часу точка пройшла половину кола радіуса . Обчислити за цей час:

а) середнє значення модуля швидкості ;

б) модуль середнього вектора швидкості ;

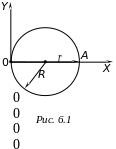в) модуль середнього вектора повного прискорення , якщо точка рухалася із сталим тангенціальним прискоренням.

Розв’язання:

Середнє значення модуля швидкості:

, (6.1)

де – довжина дуги 0А (див. рис. 6.1), тобто шлях, який точка пройшла за час . За умовою задачі . Тоді вираз (6.1) набуває вигляду:

. (6.2)

Після підстановки в (6.2) числових значень дістанемо:

.

Середній вектор швидкості:

. (6.3)

Оскільки а , то модуль середнього вектора швидкості

. (6.4)

Після підстановки числових значень у формулу (6.4) знайдемо модуль середнього вектора швидкості:

.

Середній вектор повного прискорення:

, (6.5)

оскільки , і, відповідно, .

Модуль середнього вектора повного прискорення:

, (6.6)

оскільки .

Якщо тангенціальне прискорення є сталим, модуль вектора швидкості зростає лінійно, а у цьому випадку

, і .

Тоді формула (6.6) набуде вигляду:

. (6.7)

Підставивши числові значення в формулу (6.7), дістанемо

.

Задачі для самостійного розв’язування

1. Частинка пройшла за деякий час кола з середнім значенням модуля швидкості . Знайти модуль середньої швидкості частинки за той самий час.

Відповідь: .

Приклад 7

Невеличке тіло (матеріальна точка) кинули з точки 0 під кутом  до горизонту з початковою швидкістю (рис. 7.1). Нехтуючи опором повітря, знайти:

1. тривалість польоту ;

2. дальність польоту l;

3. найбільшу висоту підняття тіла h;

4. рівняння траєкторії y(x);

5. радіус кривини траєкторії R у точках 0 и 0′;

6. середнє значення швидкості за перші t секунд польоту.

Розв’язання:

На тіло діє тільки сила тяжіння, яка надає йому прискорення вільного падіння, що дорівнює . Проекція вектора на вісь х . Оскільки і , то . З рис. 7.1 випливає, що проекція швидкості на вісь х

. (7.1)

Оскільки і, враховуючи (7.1),

.

,

оскільки на момент початку відліку часу , .

Тоді координата х змінюється з часом за законом:

. (7.2)

Проекція вектора на вісь y , тоді і .

.

Оскільки проекція швидкості на вісь у на момент початку відліку часу

,

що випливає з рисунку 7.1, то .

І залежність від часу проекції швидкості на вісь у має вигляд:

. (7.3)

.

.

Оскільки , то .

Після інтегрування здобудемо закон, за яким змінюється з часом координата у:

. (7.4)

Оскільки на момент падіння координата у дорівнює нулю, то рівняння (7.4) набуває вигляду:

.

Тоді тривалість польоту

. (7.5)

Дальність польоту . Після підстановки значення τ з (7.5) у формулу (7.2) здобудемо: .

Щоб отримати рівняння траєкторії, виразімо t з формули (7.2)

й підставимо у (7.4 )

. (7.6)

Рівняння (7.6) – рівняння параболи (Див. рис. 7.1).

Радіус кривини траєкторії тіла знайдемо з виразу для нормального при скорення

. (7.7)

Радіус кривини

. (7.8)

З рис. 7.2 випливає, що у точці 0 (на момент початку відліку часу) швидкість , нормальне прискорення , і радіус кривини траєкторії тіла

.

У верхній точці траєкторії (точці , і (див. рис. 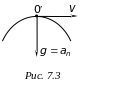7.3). Нормальне прискорення . Тоді радіус кривини траєкторії тіла у точці 0′

.

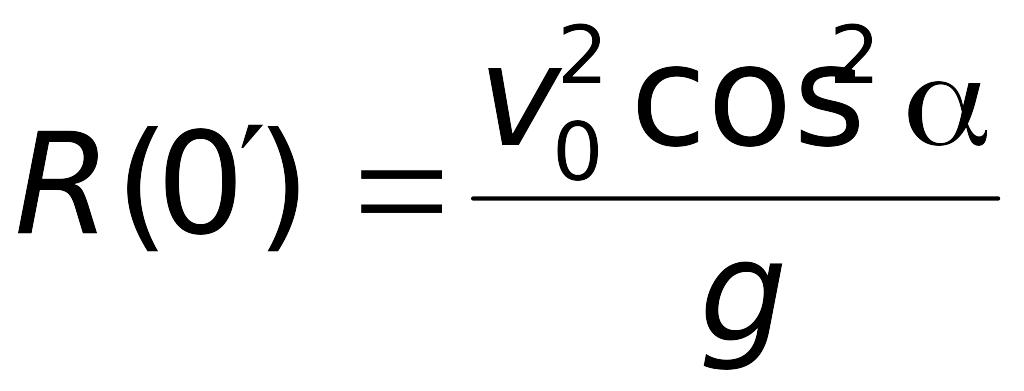Середнє значення швидкості за перші t секунд польоту

, (7.9)

оскільки .

Радіус-вектор

Після підстановки здобутого виразу для радіуса-вектора у формулу (7.9) знайдемо середнє значення швидкості за перші секунд польоту

.