Задачі для самостійного розв’язування
Визначити
максимальну частку
кінетичної енергії, яку зможе передати
частинка маси
г
при пружному зіткненні з частинкою маси
г,
яка до зіткнення перебувала у спокої.
Відповідь:
.
Приклад 8
Планета
рухається по коловій орбіті. Знайти
зв’язок між радіусом орбіти
і періодом
обертання планети навколо Сонця.
Розв’язання:
Між планетою і Сонцем діє сила тяжіння
, (8.1)
де – маса планети, – маса Сонця, – гравітаційна стала, – радіус орбіти. Період обертання
, (8.2)
де – швидкість планети. Сила тяжіння надає планеті нормального прискорення:
.
(8.3)
Нормальне прискорення зв’язане з лінійною швидкістю співвідношенням:
. (8.4)
З (8.3) та (8.4) здобудемо швидкість:
. (8.5)
З формул (8.2) та (8.4) дістанемо шукане співвідношення між періодом обертання і радіусом орбіти:
.
Отже,
квадрат періода обертання планети є
пропорційним кубові радіуса її орбіти.
Коефіцієнт
не залежить від маси планети, а залежить
від маси Сонця.
4.4. Динаміка твердого тіла
Момент сили відносно точки О (полюса):
,
де – радіус-вектор, проведений з точки О у точку прикладання сили.
Головний момент системи сил (вислідний момент) відносно полюса О:
,
де – радіус-вектор, проведений з полюса у точку прикладання сили .
Момент імпульсу (момент кількості руху) матеріальної точки відносно полюса:
,
де
– радіус-вектор точки
,
– її швидкість.
Момент імпульсу матеріального тіла:
.
Основний закон динаміки для тіла, яке обертається навколо нерухомої точки:
,
де
– головний момент зовнішніх сил,
– момент імпульсу тіла.
Основний закон динаміки для тіла, яке обертається навколо нерухомої осі (осі 0z):
,
де
і
– проекції на вісь обертання векторів
моменту імпульсу
та вислідного моменту
зовнішніх сил відносно осі обертання,
– момент інерції тіла відносно осі
обертання (осі 0z),
– кутова швидкість.
Якщо
,
то
,
де – кутове прискорення.
Момент інерції тіла:
,
де
– момент інерції матеріальної точки
відносно осі 0z;
– відстань
від осі обертання до цієї точки.
Момент інерції тонкого стрижня відносно осі, яка проходить через його середину перпендикулярно довжині:
,
де – маса стрижня, – його довжина.
Момент інерції тонкого стрижня відносно осі, яка проходить через один з його кінців перпендикулярно довжині:
.
Момент инерції суцільного циліндра (диска) маси і радіуса відносно осі, яка проходить через його центр мас перпендикулярно площині основи:
.
Момент інерції тонкого кільця, обруча, труби маси і радіуса відносно осі, яка проходить через його центр перпендикулярно площині основи:
.
Момент інерції однорідної кулі маси і радіуса відносно осі, яка проходить через її центр:
.
Теорема Гюйгенса – Штейнера:
,
де
− момент інерції тіла відносно довільної
осі 0z,
– момент інерції цього самого тіла
відносно осі, паралельної даній і такої,
що проходить через центр мас тіла,
– відстань між осями.
Рух вільного (незакріпленого) твердого тіла задовольняє наступні диференціальні рівняння руху:
,
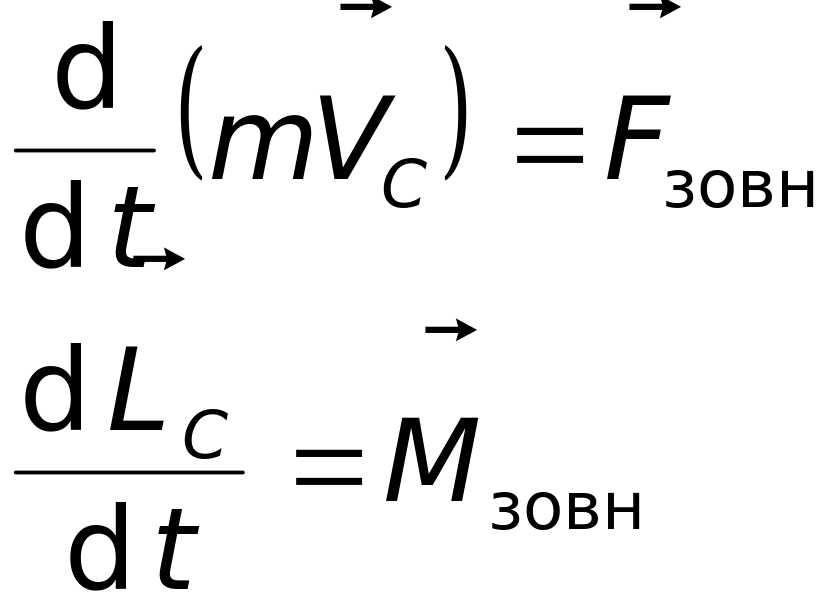де
– швидкість центра мас тіла маси
,
– сума зовнішніх сил,
– сума моментів зовнішніх сил,
– момент імпульсу тіла відносно центра
мас.
Момент імпульсу замкненої системи тіл відносно будь-якої нерухомої точки
.
Для замкненої системи у випадку обертання відносно осі 0z
.
Кінетична енергія вільного твердого тіла:
,
де
– момент інерції тіла відносно миттєвої
осі, яка проходить через його центр мас,
– швидкість поступального руху центра
мас тіла,
– маса тіла,
– кутова швидкість.
Робота сталого моменту сили , що діє на тіло, яке обертається:
,
де – кут повороту тіла.