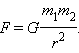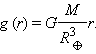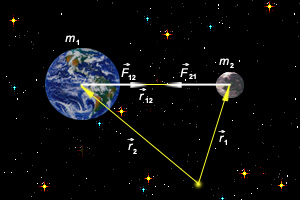
40 Исаак Ньютон смог объяснить движение тел в космическом пространстве с помощью закона всемирного тяготения. Ньютон пришел к своей теории в результате многолетних исследований движения Луны и планет.

Рисунок 3.1.1.1. Закон всемирного тяготения

Если m₁ и m₂ – массы двух точечных тел, а r – расстояние между ними, то закон всемирного тяготения записывается в виде

где G = 6,67∙10^–11 Н∙м²/кг² – гравитационная постоянная. Этот закон справедлив также для сферически симметричных тел (при расстояниях между центрами больше суммы их радиусов), а приближенно он выполняется для любых тел, если расстояние между ними велико по сравнению с их размерами.

Ускорение, которое испытывает тело m, находящееся на расстоянии r от тела M, равно 

В частности, ускорение свободного падения в поле Земли равно  , где   – масса Земли, r – расстояние до ее центра. Вблизи поверхности Земли ускорение свободного падения равно g = 9,8 м/с². Сплюснутость Земли и ее вращение приводят к отличию силы тяжести на экваторе и возле полюсов: ускорение свободного падения в точке наблюдения может приближенно высчитываться по формуле g = 9,78 ∙ (1 + 0,0053 sin φ), где φ – широта этой точки.

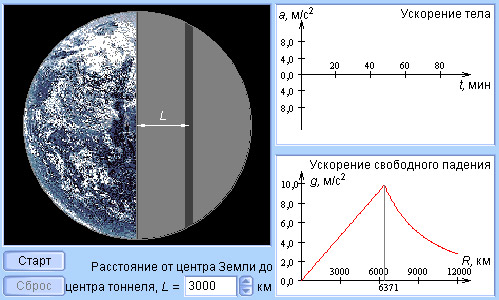
Модель 3.1. Гравитация внутри Земли

Внутри Земли, если принять ее за однородный шар, сила тяжести убывает пропорционально расстоянию до центра: 

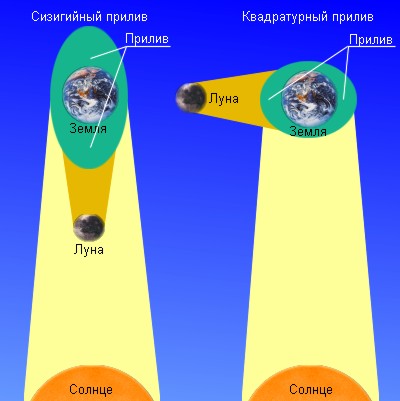
Поскольку размеры Земли не бесконечно малы по сравнению с расстояниями до Луны и Солнца, то силы лунного и солнечного притяжения в разных точках Земли разные. Так, самая близкая точка будет притягиваться сильнее, чем самая далекая точка. Действие возмущающих сил на отдельные части земной поверхности вызывает приливы и отливы. При этом приливное влияние Луны в 2,2 раза сильнее, чем Солнца.

Рисунок 3.1.1.2. Квадратурные и сизигийные приливы

Каждый день уровень океанских вод поднимается и снижается, причем в устьях некоторых рек и отдельных заливах на несколько метров. Эти явления носят название приливов и отливов. Гидросфера, как и всякое жидкое тело, способна деформироваться, что и происходит каждый день в результате притяжения Луны и Солнца. В полнолуние и новолуние тяготение Луны и Солнца усиливают действие друг друга, и приливы бывают выше средних. Когда же Луна находится в фазах первой и последней четверти, силы тяготения светил гасят друг друга, и уровень приливов ниже среднего. Перегородив дамбой залив, приливы можно использовать для получения электроэнергии.

Луна каждые 24 часа 50 минут вызывает приливы не только в океанах, но и в коре Земли, и в атмосфере. Под воздействием приливных сил литосфера вытягивается примерно на полметра. Тяготение Луны вызывает такжепрецессию земной оси.

Из-за океанских приливов и отливов возникает сила трения между литосферой и гидросферой, замедляющая скорость вращения Земли вокруг своей оси. Каждое столетие продолжительность суток увеличивается приблизительно на 0,002 с. Два миллиарда лет назад продолжительность земных суток составляла всего 10 часов, а в отдаленном будущем они будут равны одному месяцу. Уже теперь благодаря приливным силам Луна постоянно обращена к Земле одной и той же стороной. Кроме того, притяжение приливных выступов Земли увлекает Луну по орбите вперед, в результате чего она удаляется от Земли со скоростью около 3 см в год.

Именно приливные силы, возникшие в гравитационном поле Юпитера, разорвали ядро кометы Шумейкеров–Левина множество частей, после чего несколько лет назад она упала на Юпитер.

Закон всемирного тяготения справедлив только в рамках классической механики. Он, по-видимому, нарушается на малых расстояниях (порядка планковской длины). В 1916 году Альберт Эйнштейн в теории относительностипоказал, что свойства пространства и времени изменяются вблизи больших масс.

41 Ускоре́ние свобо́дного паде́ния g (обычно произносится как «Же»), — ускорение, придаваемое телу в вакууме силой тяжести, то есть геометрической суммой гравитационного притяжения планеты (или другого астрономического тела) и сил инерции, вызванных её вращением, за исключением кориолисовых сил инерции^[1]. В соответствии со вторым законом Ньютона, ускорение свободного падения численно равно силе тяжести, воздействующей на объект единичной массы.

Значение ускорения свободного падения на поверхности Земли обычно принимают равным 9,8 или 10 м/с². Стандартное («нормальное») значение, принятое при построении систем единиц, g = 9,80665 м/с²^[2], а в технических расчётах обычно принимают g = 9,81 м/с².

Стандартное значение g было определено как «среднее» в каком-то смысле ускорение свободного падения на Земле, примерно равно ускорению свободного падения на широте 45,5° на уровне моря.

Реальное ускорение свободного падения на поверхности Земли зависит от широты, времени суток и других факторов. Оно варьируется от 9,780 м/с² на экваторе до 9,832 м/с² на полюсах^[3]. Оно может быть вычислено (в м/с²) по эмпирической формуле:

где   — широта рассматриваемого места,   — высота над уровнем моря в метрах.^[4] Эта формула применима лишь в ограниченном диапазоне высот от 0 до нескольких десятков км, где убывание ускорения свободного падения с высотой можно считать линейным (на самом же деле оно убывает квадратично).

42 Поступательное движение — это механическое движение системы точек (тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени.[1]

Приведённая иллюстрация показывает, что, в отличие от распространённого утверждения [2]. поступательное движение не является противоположностью движению вращательному, а в общем случае может рассматриваться как совокупность поворотов — не закончившихся вращений. При этом подразумевается, что прямолинейное движение есть поворот вокруг бесконечно удалённого от тела центра поворота.

В общем случае поступательное движение происходит в трёхмерном пространстве, но его основная особенность — сохранение параллельности любого отрезка самому себе, остаётся в силе.

Математически поступательное движение по своему конечному результату эквивалентно параллельному переносу.Однако, рассматриваемое как физический процесс оно представляет собой в трёхмерном пространстве вариант винтового движения (См. Рис. 2)