1Механическое движение-это тела называються изменения его положения в пространстве относительно других тел с течением времени, при этом тела взаимодействуют по закону механики.

2 Кинема́тика (греч. κινειν — двигаться) в физике — раздел механики, изучающий математическое описание (средствами геометрии, алгебры, математического анализа…) движения идеализированных тел (материальная точка, абсолютно твердое тело, идеальная жидкость), без рассмотрения причин движения (массы, сил и т. д.). Исходные понятия кинематики — пространство и время. Например, если тело движется по окружности, то кинематика предсказывает необходимость существования центростремительного ускорения без уточнения того, какую природу имеет сила, его порождающая. Причинами возникновения механического движения занимается другой раздел механики — динамика.

3 Поступательное движение — это механическое движение системы точек (тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени.[1]

4 Система отсчёта — это совокупность тела отсчета, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение (или равновесие) каких-либо материальных точек или тел[1][2].

Математически движение тела (или материальной точки) по отношению к выбранной системе отсчёта описывается уравнениями, которые устанавливают, как изменяются с течением времени t координаты, определяющие положение тела (точки) в этой системе отсчёта. Эти уравнения называются уравнениями движения. Например, в декартовых координатах х, y, z движение точки определяется уравнениями , , .

В современной физике любое движение является относительным, и движение тела следует рассматривать лишь по отношению к какому-либо другому телу (телу отсчёта) или системе тел. Нельзя указать, например, как движется Луна вообще, можно лишь определить её движение, например, по отношению к Земле, Солнцу, звёздам и т. п.

5 Траекто́рия материа́льной то́чки — линия в трёхмерном пространстве, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве.[1]. Существенно, что понятие о траектории имеет физический смысл даже при отсутствии какого-либо по ней движения.

6 Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением.

7 при поступател.движении движутся по лдинаковым траекториям и имеют одинаковые скорость и ускорение в данныи момент времени

8 Сре́дняя ско́рость — в кинематике некая усреднённая характеристика скорости частицы за время её движения.?

9 Мгновенная скорость (обычно используется термин скорость) характеризует быстроту изменения радиуса-вектора материальной точки во времени. Она равна перемещению тела S = dr за единицу времени dt применительно к данному моменту движения V = dr/dt. Численное значение скорости равно V = dr /dt. Скорость направлена по касательной в данной точке траектории. Ее значение определяется тангенсом угла наклона, который образует касательная к кривой x = f(t) в заданный момент времени с осью Ot

10 Мгновенное ускорение (обычно используется термин ускорение) характеризует быстроту изменения скорости материальной точки во времени. Оно равно отношению изменения скорости тела к величине бесконечно короткого временного интервала, за который это изменение произошло, применительно к данному моменту движения a = dV/dt. Ускорение может быть сориентировано к траектории под произвольным углом в зависимости от характера движения.

11

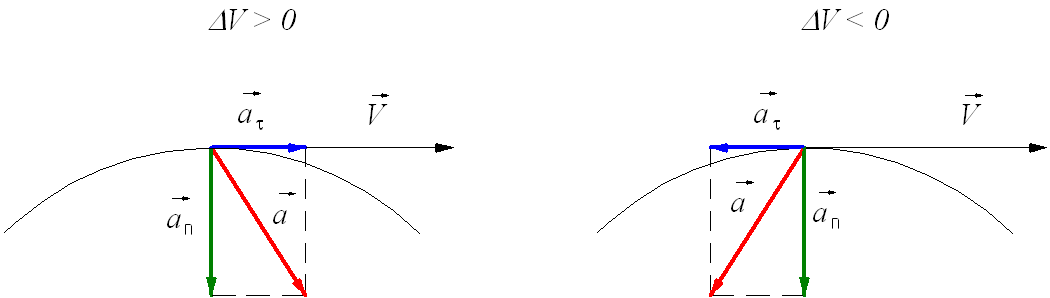
Изменение скорости по велечине и направлению, представляет собой векторную сумму тангенциального и нормального ускорений.

12 Километр в секунду, Километр в час, Метр в секунду

13 Гал (единица измерения), Метр в секунду в квадрате

14 Нормальное ускорение

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой n. Вектор нормального ускорения направлен по радиусу кривизны траектории.

15 Быстрота изменения направления касательной к траектории определяется скоростью движения точки по окружности и степенью искривленности траекторий.

Степень искривленности плоской кривой характеризуется кривизной С.

Радиус кривизны r – радиус такой окружности, которая сливается с кривой в данной точке на бесконечно малом ее участке dS.

Центры таких окружностей – центры кривизны т. O и O' (рис. 2.10)

Скорость изменения направления касательной можно выразить как произведение скорости изменения угла на единичный вектор, показывающий направление изменения угла:

где – единичный вектор, направленный перпендикулярно касательной в данной точке, т.е. по радиусу кривизны к центру кривизны.

Из (2.3.10) следует, что , но т.к. dS = vdt, то .

Тогда и, следовательно ; наконец, , т.е.

Нормальное ускорение показывает быстроту изменения направления вектора скорости. Модуль нормального ускорения равен

Термин "центростремительное ускорение" используется в случае, когда движение происходит по окружности. Если же движение происходит по произвольной кривой, то соответствующим аналогом является термин "нормальное ускорение" (перпендикулярное к касательной в любой точке траектории).

Итак, возвращаясь к выражению (2.3.8), можно записать, что суммарный вектор ускорения при движении точки вдоль плоской кривой равен:??????????????????????

16 Вращательным движением называется такое движение, при котором все точки некоторой прямой линии (оси), взятой в этом теле, остаются неподвижными.

17 Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

,

18 Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.

При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно^[1]:

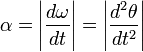
Вектор углового ускорения   направлен вдоль оси вращения (в сторону   при ускоренном вращении и противоположно   — при замедленном).

При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости   по времени^[2], то есть

,

и направлен по касательной к годографу вектора   в соответствующей его точке.

Существует связь между тангенциальным и угловым ускорениями:

,

где R — радиус кривизны траектории точки в данный момент времени. Итак, угловое ускорение равно второй производной от угла поворота по времени или первой производной от угловой скорости по времени. Угловое ускорение измеряется в рад/с

19 Период обращения - это время, за которое совершается один оборот.

Если, например, за время t = 4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой Т и определяется по формуле:

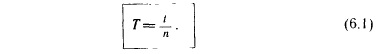
Итак, чтобы найти период обращения, надо время, за которое совершено п оборотов, разделить на число оборотов. 20 Частота обращения - это число оборотов, совершаемых за 1 с. Если, например, за время t = 2 с тело совершило n = 10 оборотов, то легко сообразить, что за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой V (читается: ню) и определяется по формуле:

Итак, чтобы найти частоту обращения, надо число оборотов разделить на время, в течение которого они произошли.

21 Динамика – раздел механики, изучающий законы взаимодействия тел.

22 Си́ла — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная кмассивному телу сила является причиной изменения его скорости или возникновения в нём деформаций.^[1]

23 Ма́сса (от греч. μάζα) — скалярная физическая величина, одна из важнейших величин в физике. Первоначально (XVII—XIX века) она характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе (инертность), так и гравитационные свойства — вес. Тесно связана с понятиями «энергия» и «импульс» (по современным представлениям — массаэквивалентна энергии покоя).

24Первый закон Ньютона

Основная статья: Инерция

Первый закон Ньютона постулирует наличие такого явления, как инерция тел. Поэтому он также известен как Закон инерции. Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения тела, на него необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают инертностью. Инертность — это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тела.

Современная формулировка

В современной физике первый закон Ньютона принято формулировать в следующем виде^[1]:

Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго.

Закон верен также в ситуации, когда внешние воздействия присутствуют, но взаимно компенсируются (это следует из 2-го закона Ньютона, так как скомпенсированные силы сообщают телу нулевое суммарное ускорение).

Историческая формулировка

Ньютон в своей книге «Математические начала натуральной философии» сформулировал первый закон механики в следующем виде:

Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

С современной точки зрения, такая формулировка неудовлетворительна. Во-первых, термин «тело» следует заменить термином «материальная точка», так как тело конечных размеров в отсутствие внешних сил может совершать и вращательное движение. Во-вторых, и это главное, Ньютон в своём труде опирался на существование абсолютной неподвижной системы отсчёта, то есть абсолютного пространства и времени, а это представление современная физика отвергает. С другой стороны, в произвольной (скажем, вращающейся) системе отсчёта закон инерции неверен. Поэтому ньютоновская формулировка нуждается в уточнениях.