Из графиков видно, что выполняются соотношения для характеристик
что соответствует сделанному ранее предположению.
На
рис. 6 показаны графики зависимостей
для исследуемых систем.
Рис.
6. Графики зависимостей среднего времени
простаивания в очереди 
от интенсивности входящего потока запросов , для трех
исследуемых систем, в установившемся режиме работы
На
рис. 6 величина 
– среднее
время простаивания в очереди для i-й
системы. Из графиков видно, что значение
монотонно возрастает с увеличением
интенсивности входящего потока
при
;
при
близком к
функция
имеет локальный максимум. При приближении
величины
к значению
на некотором интервале среднее время
простаивания в очереди убывает, так как
возрастает вероятность нахождения
системы в режиме работы со вторым
сервером. При
близком к
функция
неограниченно возрастает. При
система уже не в состоянии обработать
входящий поток запросов, и характеристику
определить нельзя. Также из графиков
видно, что выполняется соотношение
что соответствует сделанному ранее предположению.
На
рис. 7 показаны графики зависимостей
для исследуемых систем.
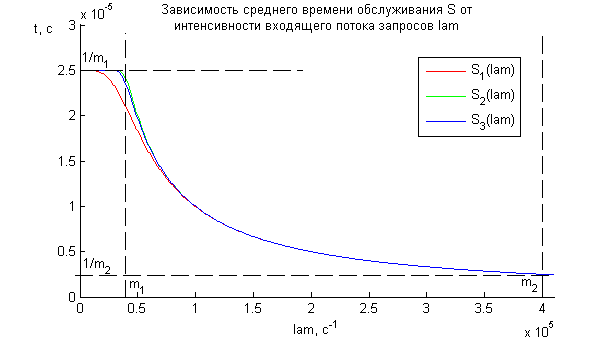
Рис.
7. Графики зависимостей среднего времени
обслуживания 
от интенсивности входящего потока запросов , для трех
исследуемых систем, в установившемся режиме работы
На
рис. 7 величина 
– среднее
время обслуживания для i-й
системы. Из графика видно, что при
на некотором интервале среднее время
обслуживания не изменяется и равно
приблизительно 
,
так как система работает преимущественно
в режиме с первым сервером. При приближении
величины
к значению
среднее время обслуживания монотонно
убывает и стремится к величине 
,
так как увеличивается вероятность
нахождения системы в режиме работы со
вторым сервером. Также из графиков
видно, что выполняется соотношение
что соответствует сделанному ранее предположению.
Вычислим характеристики работы систем, параметры которых определены в таблице 1, для двух заданных значений интенсивности входящего потока запросов к серверу . Результаты вычислений представлены в таблице 2.
Таблица 2:
Характеристики работы системы при
различной интенсивности входящего
потока 
|
|
|
|
System #1 |
|
|
|
|
|
|
|
|
|
|
|
System #2 |
|
|
|
|
|
|
|
|
|
|
|
System #3 |
|
|
|
|
|
|
|
|
|
|
|
В таблице 2 величины , , – характеристики i-й системы: среднее количество запросов в системе, среднее время простаивания в очереди, среднее время обслуживания, соответственно.
Также
построим для заданных значений
интенсивности входящего потока графики
распределения случайной
величины N
(количества находящихся в системе
запросов) и проверим соответствие
распределений полученным выше значениям
Рис. 8. Стационарное распределение вероятности количества находящихся
в системе запросов при интенсивности входящего потока
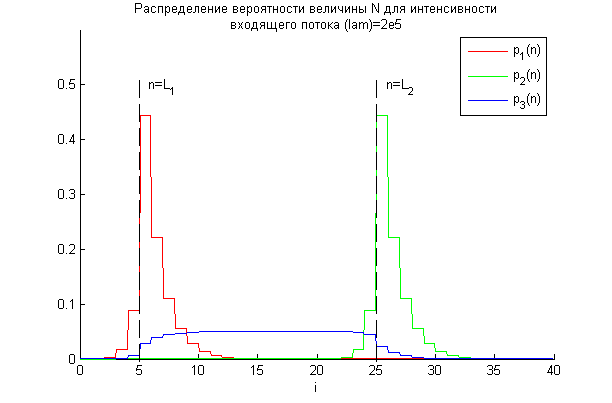
Рис. 9. Стационарное распределение вероятности количества находящихся
в системе запросов при интенсивности входящего потока
На
рис. 8, 9 величина 
– стационарная вероятность нахождения
i-й
системы в состоянии n
при заданной интенсивности входящего
потока.
|
(31) |
Из
графиков видно, что при 
(рис. 8)
вероятность нахождения системы в режиме
работы первым сервером для всех
исследуемых систем выше вероятности
нахождения системы в режиме работы со
вторым сервером. Это объясняется тем,
что при данном значении
переход в режим работы с кешированием
приводит к быстрому уменьшению длины
очереди и возвращению в режим работы
без кеширования. При 
(рис. 9)
функции распределения для систем с
одноуровневым управлением имеют ярко
выраженный максимум вблизи значений
n,
равных заданным для систем параметрам
L.
Функции распределения для системы с
гистерезисным управлением не имеет
ярко выраженного максимума, т.е. дисперсия
величины N
значительно выше.
Характер графиков распределения при позволяет сделать следующий вывод: система с одноуровневым управлением при высокой интенсивности входящего потока будет большую часть времени находиться в состоянии, при котором длина очереди N близка к
значению L. Это означает, что в системе будет происходить частое переключение из одного режима работы в другой, которое может негативно сказаться на динамических характеристиках системы при наличии временных затрат на переключение. Система с гистерезисным управлением лишена указанного недостатка, поскольку переключение между режимами работы происходит при различных значениях N.
Анализ графиков показывает, что значения средней длины очереди , вычисленные и приведенные в таблице 2, соответствуют распределениям вероятностей длины очереди N.
Выполним
проверку выполнения условия 
.
Проверка для системы с одноуровневым управлением:
sum1=0;
for i=0:500
sum1=sum1+odnourP(i, lamb, m_1, m_2, L_low);
end
sum1
Проверка для системы с гистерезисным управлением:
sum2=0;
for i=0:500
sum2=sum2+gisterP(i, lamb, m_1, m_2, L_1, L_2);
end
sum2
Результат преверки:
sum1 =
1
sum2 =
1.0000
Результат подтверждает выполнение условия равенства суммы стационарных вероятностей единице.