Vychmat_lektsii / Лекция 10 продолжение УЧП

9

Лекция 10

Пример УЧП:

Поперечные колебания струны.

Струной называется тонкая нить , работающая на растяжение(не на изгиб).

Пусть Т – сила напряжения в струне (постоянна в любой точке), ρ- линейная плотность массы. Концы струны закреплены в точках а и b .

Н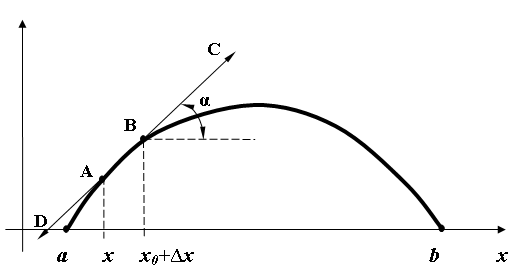еобходимо найти функцию u=u(x,t) отклонения струны от оси абсцисс под действием силы.

Будем считать отклонение u=u(x,t) малым.

На элемент ∆x струны от точки А до точки В действуют две силы : натяжения - и

Можно видеть :

В силу малости можно произвести замену

Сумма проекций сил на ось Ou тогда будет :

С другой стороны , согласно второму закону Ньютона сила , действующая на элемент ∆x струны по направлению оси Ou будет равна:

Тогда из условий равновесия имеем:

Получили уравнение поперечных колебаний струны в отсутствие внешних сил, т.е. уравнение свободных колебаний.

Граничные и начальные условия для УЧП.

1. Пусть уравнение параболического типа , т.е.

В физических задачах переменная x играет роль пространственной координаты , а вторая независимая переменная – роль времени , поэтому t .

Для обеспечения единственности решения и корректности задачи требуется задать краевые и начальные условия.

Рассмотрим частый случай , когда a(x,t)∙e(x,t)<0, т.е. имеют разные знаки.

Требуется найти решение в прямоугольнике

Причем есть начальное условие u(x,0)=φ₀(x), 0≤x≤l , где φ₀(x) заданная функция в начальный момент времени t=0 . Tакже налагаются краевые условия при x=0 и x=l :.

Например , это уравнение может описывать изменение температуры в однородном стержне длины l , краевые условия означают , что температура в начальном и конечном сечениях задана и поддерживается постоянной.

Геометрический смысл решения есть некая поверхность u(x,t) , которая проецируется на область D плоскости , причем заданы три кривые, которые есть края этой поверхности u(x,t) и которые проецируются на нижнюю и боковые стороны прямоугольника D. Внутри прямоугольника и на его верхней стороне значения u(x,t) неизвестны , значит неизвестна сама форма поверхности и ее требуется найти .

С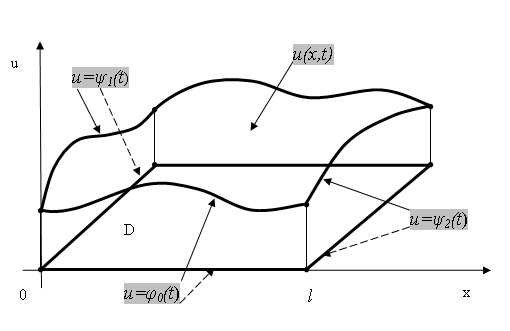плошными стрелками показаны краевые функции в пространстве, ограничивающие поверхность u(x,t) , пунктирными стрелками показаны их проекции на стороны прямоугольника D.

2. Если уравнение гиперболического типа

Т.е. имеем :

a(x,t)>0.

Также будем рассматривать прямоугольник

Начальные условия здесь

φ ₀(x) , φ₁(x) – заданные функции .

В изменение рисунка геометрической интерпретации надо на нижнюю сторону добавить проекцию

Оба рассмотренных типа уравнений описывают нестационарные процессы .

3. Если уравнение эллиптического типа , то оно имеет вид :

Уравнение такого типа обычно описывает физический процесс, в котором обе независимых переменных равноправны и есть по сути пространственные координаты, т.е. эллиптические уравнения еще называют стационарными уравнениями математической физики.

Здесь требуется задавать дополнительные краевые условия по всему периметру прямоугольника

Геометрически здесь получим:

Здесь по всему периметру заданы кривые , на которые опирается поверхность u(x,t) , а внутри прямоугольника u(x,t) надо найти решая краевую задачу.

Одним из часто используемых методов численного решения УЧП является МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ или МЕТОД СЕТОК.

В основе метода лежит идея замены производных конечно-разностными соотношениями.

Методы построения консервативных разностных схем основаны на законах сохранения , свойственных большинству физических процессов. Для конструирования таких схем исходят из уравнений балансов , записанных для отдельной ячейки сеточной области , с последующим использованием квадратурных и интерполяционных формул.

Построенные разностные уравнения по всем точкам сеточной области удовлетворяют дискретным аналогам интегральных законов сохранения.

П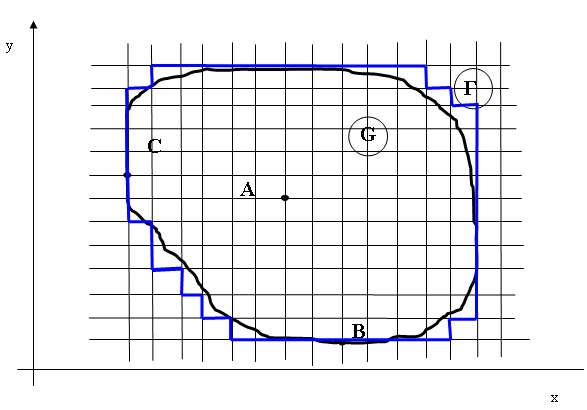усть в плоскости xOy имеется некоторая область G с границей Г.

Построим два семейства параллельных прямых :

Точки пересечения прямых называются узлами.

Узлы соседние – удаление их друг от друга не расстояние , равной шагу сетки в соответствующем направлении ( h или l ).

Рассмотрим область G+Г и все узлы, расположенные на расстоянии , меньшем чем шаг от границы Г .

Узлы внутренние, у которых все четыре соседних принадлежат области G ( узел А ) . Оставшиеся называют граничными ( узлы В , С ) . Значения искомой функции u=u(x,y) в узлах сетки будем обозначать через

В каждом внутреннем узле заменим частные производные разностными соотношениями ( центральными):

В граничных узлах используются менее точные формулы ( правые) :

Для производных второго порядка :

Выполненные замены позволяют свести решение уравнений с частными производными к решению системы разностных уравнений.

Метод сеток для задачи Дирихле.

Задача Дирихле для уравнения Пуассона или первая краевая задача

Формулировка: Найти функцию u=u(x,y), удовлетворяющую внутри некоторой области G уравнению Пуассона , а на границе Г- условию

Заменяем исходное уравнение конечно-разностными соотношениями :

Это вместе со значениями u_ik в граничных узлах есть система линейных алгебраических уравнений относительно значений функции u=u(x,y) в узлах сетки. Самый простой вид эта система имеет в прямоугольной области , а еще лучше в квадратной.

Система уравнений тогда может быть записана в виде:

u_i+1,k+ u_i-1,k+ u_i,k+1+ u_i,k-1-4 u_ik=h²f_ik

Когда f(x,y)=0 будем иметь уравнение Лапласа. Уравнение для внутреннего узла будет такое:

Схемы расположения узлов может изменяться, тогда будут меняться и уравнения:

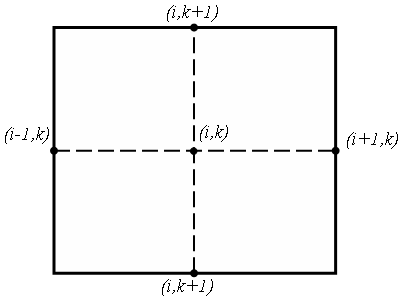
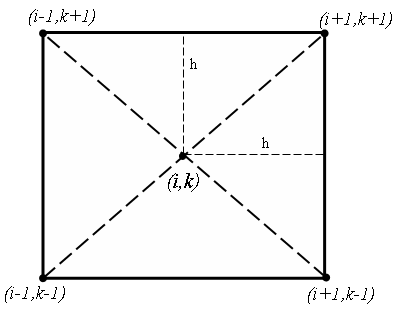
Уравнение Лапласа

Уравнение Пуассона

Погрешность можно оценить по формуле :

Погрешность приближенного решения , полученного разностным методом, складывается из трех погрешностей:

1. погрешность замены дифференциального уравнения разностным

2. погрешности аппроксимации краевых условий

3. погрешности в результате решения системы разностных уравнений приближенным методом.

Пример:

Задача об упругой деформации квадратной пластины под действием постоянной силы с нулевыми краевыми условиями ∆u=-1 .

Пусть сторона квадрата равна 1 и шаг h =0,25 .

Здесь полная симметрия искомой функции , т.к. все краевые условия нулевые , а правая часть уравнения постоянна . Поэтому достаточно рассматривать лишь четверть квадрата:

П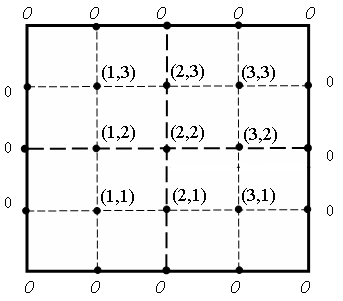олучаем уравнения :

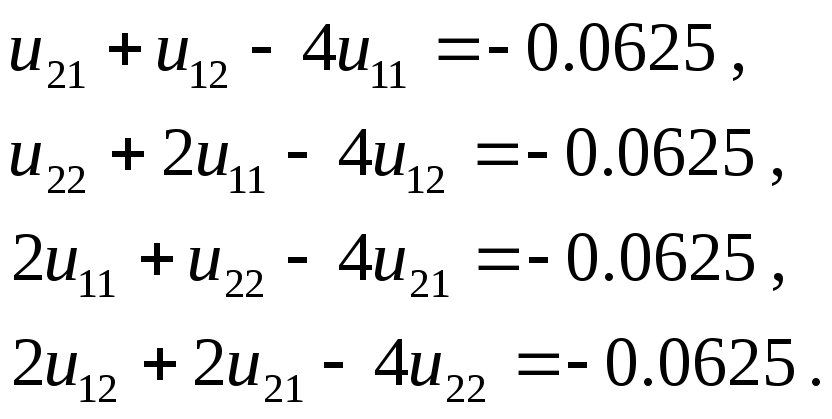
С учетом симметрии u₁₂=u₂₁

В итоге имеем решение в узлах :

Решение краевых задач для криволинейных областей.

Если граница Г области G криволинейна , то в этом случае алгоритм решения задачи методом конечных разностей в целом сохраняется , но возникают трудности , связанные с аппроксимацией производных в приграничных узлах. При этом надо учитывать , что расстояния от крайнего внутреннего узла до непосредственно расположенного на границе все разные . При составлении вычислительной программы все эти условия вызывают дополнительные трудности , поэтому в исходном уравнении используют замену независимых переменных , т.е. переходят к криволинейной системе координат.

Типы сеток:

1. регулярные

2. нерегулярные

3. прямоугольные

4. полярные

5. скошенные

6. изменение размеров клеток сетки которых подчинено какому-то закону

Свойства разностных схем для УЧП , аппроксимация , устойчивость и сходимость.

Для разного типа уравнений в частных производных используются разные подходы к построению аппроксимирующей сетки , но можно сформулировать общую схему решения краевых задач математической физики:

Пусть задан некоторый дифференциальный оператор второго порядка ∆u , который является линейным ( ∆(c₁u₁+ c₂u₂)= c₁∆u₁+ c₂∆u₂ ) для любых дважды дифференцируемых функций u_1, u₂ и действительных чисел с₁,и с₂ .

В область определения уравнения ∆u=f вводится прямоугольная вычислительная сетка и аппроксимируется конечно-разностным оператором ∆_hτu .Т.о. справедливо равенство :

∆u=∆_hτu+α_h,τ , где α_h,τ - погрешность аппроксимации.

Правило:

Разностная схема удовлетворяет свойству дифференциального оператора , если погрешность α_h,τ стремится к нулю при неограниченном измельчении сетки.

Погрешность приведенных примеров O(h²+τ) или O(h²+τ²) .

9

стр. из 9