Vychmat_lektsii / Лекция 13 Инт. уравнения

Лекция 13

Численные методы решения интегральных уравнений.

Определение:

Уравнение относительно неизвестной функции , содержащейся под знаком интеграла называется интегральным уравнением.

В общем виде интегральное уравнение может быть записано в виде:

D- некоторая область n-мерного пространства

y(s)- неизвестная функция

f(x)- известная функция

Q – функция относительно x (линейная или нелинейная).

Интегральные уравнения широко используются в теории упругости, газовой динамике , электродинамике, экологии , других , где они есть следствие законов сохранения массы, импульса и энергии..

Достоинство: интегральные уравнения не содержат производных искомой функции и следовательно жесткие ограничения на гладкость решения отсутствуют .

Примеры интегральных уравнений:

1. Зависимости между напряжениями σ и деформациями ε

в упруго-вязких средах :

E - модуль упругости , K(t-τ) - функция влияния напряжения σ(t) в момент времени τ на деформацию ε(t) в момент времени t

T(t-τ) - функция влияния деформации ε(t) в момент времени τ на напряжение σ(t) в момент времени t

Далее ограничимся рассмотрением одномерных линейных интегральных уравнений (ОЛИУ) , в которых функция y(x) является функцией , зависящей от одной переменной , а область D – отрезком конечной длины , в каждой точке которого подынтегральная функция Q(x,s,y(s)) представима в виде K(x,s)y(s).

Классификация типов ЛИУ проводится по виду верхней границы интеграла:

1. Уравнение Фредгольма – верхняя граница интегрирования постоянна,

2. Уравнение Вольтерры - верхняя граница интегрирования переменна.

Каждое из перечисленных типов уравнений может быть первого либо второго рода:

1. Уравнение Фредгольма первого рода

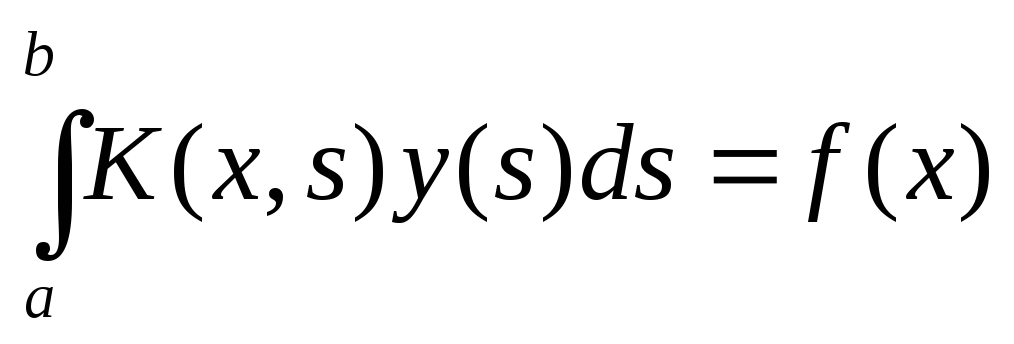
Уравнение Фредгольма второго рода

2. Уравнение Вольтерры можно записать в общем виде

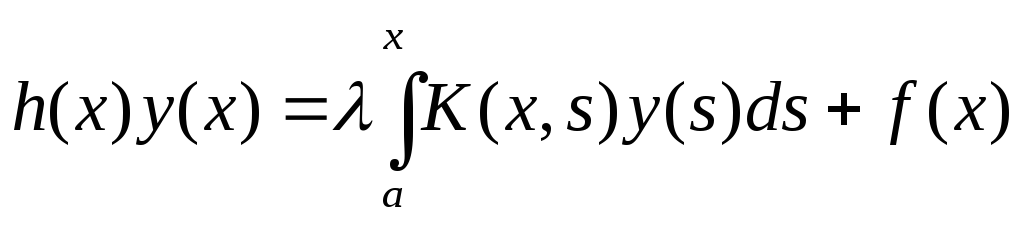
Где h(x)- множитель в зависимости от рода уравнения,

f(x) –известная функция ,

y(x) – решение уравнения ,

K(x,s) – ядро интегрального уравнения .

На практике чаще применяются уравнения второго рода.

Ядро интегрального уравнения Фредгольма определяется на множестве точек квадрата [a,b][a,b], а уравнения Вольтерра – в треугольнике а≤s≤x≤b

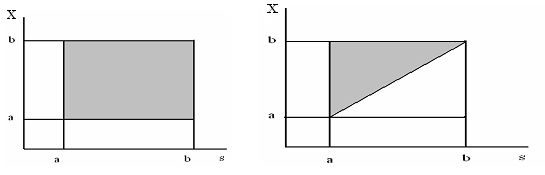
Надо заметить , что если доопределить ядро K(x,s) уравнения Вольтерры нулем , то в треугольнике а≤s≤x≤b уравнение Вольтерры можно считать уравнением Фредгольма и использовать соответствующие методы решения.

Однако при этом надо понимать , что могут быть упущены некоторые специфические особенности первоначального уравнения Вольтерры , поэтому все же надо решать эти два типа уравнений раздельно.

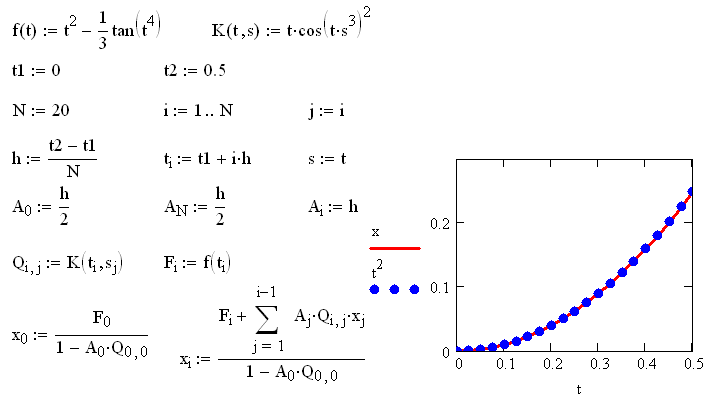
Рассмотрим численные методы решения интегральных уравнений , в основе которых лежит замена интеграла в ЛИУ конечной суммой при помощи какой-либо квадратурной формулы. Такое действие позволяет свести решение исходной задачи к решению СЛАУ, число ЛАУ определяется числом узлов временной сетки. Такие методы называются квадратурными или методами конечных сумм.

Если такие методы применяются при решении НеЛИУ , то получаем для последующего решения НеСЛАУ .

Квадратурный метод решения ИУ Фредгольма.

Рассмотрим решение ИУ Фредгольма первого и второго рода.

Заменим определенный интеграл приближенным значением :

Где x_j – абсциссы точек отрезка [a,b],

A_j - весовые коэффициенты квадратурной формулы не зависящие от F(x).

Введем на отрезке [a,b] дискретную сетку x₁,x₂,x₃,..x_n узлы которой совпадают с узлами s₁,s₂,s₃,..s_n .

Теперь используем это равенство в преобразовании уравнений Фредгольма первого и второго рода соответственно:

Здесь

Получаем функцию , описывающую приближенное решение ИУ .

Данную систему можно решить каким-либо известным способом( методом Гаусса , итераций).

Таким образом алгоритм решения уравнения Фредгольма :

1. Задать сетку x_i

2. Вычислить значения функции f(x)в узлах сетки

3. Вычислить элементы матрицы, составленной из коэффициентов СЛАУ

4. Решить СЛАУ

В зависимости от выбора квадратурной формулы значения коэффициентов A_j и абсцисс точек отрезка [a,b] x_j будут такими :

• Для формулы трапеций

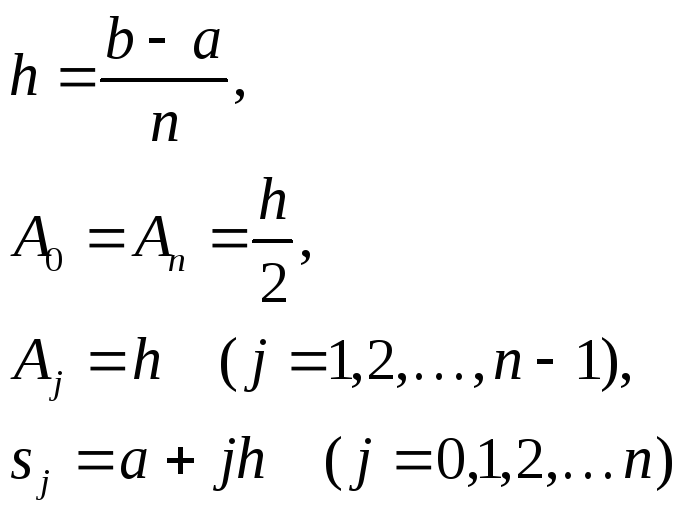
• Для формулы Симпсона

Погрешность приближенного решения есть погрешность выбранной квадратурной формулы.

Пример:

Найти приближенное решение уравнения

Используем формулу Симпсона при n=2.

Сначала определим коэффициенты:

Теперь можем написать:

Вспомним , что x=x_i ( та же сетка ) :

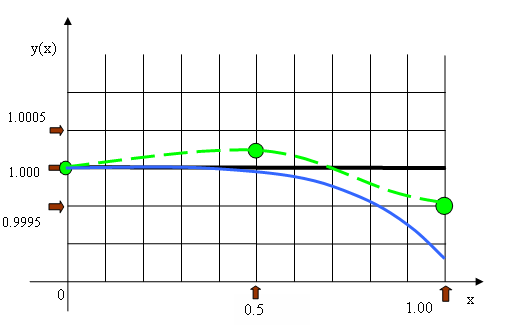
Получаем решение : Точным решением уравнения является функция y(x)1

Окончательное приближенное решение интегрального уравнения Фредгольма первого рода записывается в виде интерполяционного полинома, а второго рода в виде :

В итоге получаем приближенное решение:

Метод замены ядра на вырожденное

Продолжаем рассмотрение уравнения Фредгольма второго рода.

Ядро K(x,s) называется вырожденным , если оно может быть представлено в виде: , где коэффициентные функции линейно-независимы на [a,b].

Метод основан на положении , что в этом случае может быть получено точное решение. Первоначальное ядро приближенно заменяем на вырожденное:

В качестве вырожденного ядра можно взять отрезок ряда Тейлора или ряда Фурье для функции K(x,s).

Квадратурный метод решения интегральных уравнений Вольтерры.

Рассмотрим интегральное уравнение Вольтера второго рода.

Имеем: x [a,b]

В данном случае если ядро есть непрерывная функция в прямоугольнике D , а f(x) непрерывна на отрезке [a,b] , то решение будет единственным при любом λ .

Возьмем какую-либо квадратурную формулу Ньютона-Котеса:

Где x_j – абсциссы точек отрезка [a,b],

A_j - весовые коэффициенты квадратурной формулы

Формально это уравнение тоже может рассматриваться как уравнение Фредгольма с ядром вида :

Тогда для нахождения численного решения можно воспользоваться уже полученными результатами, только здесь в силу свойств ядра СЛАУ вырождается в треугольную :

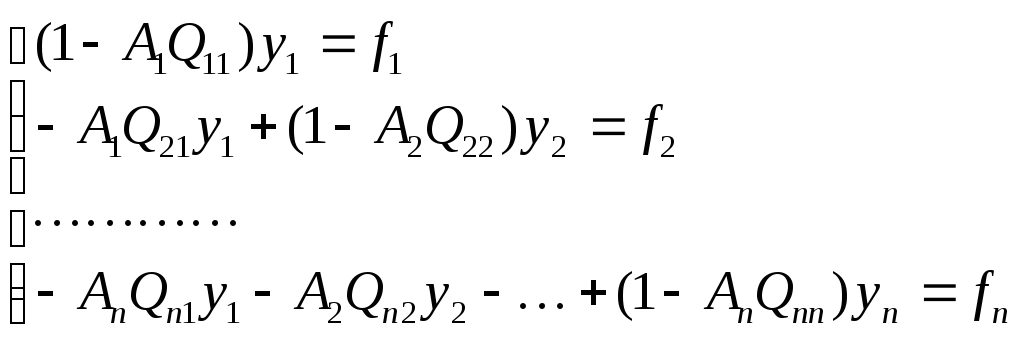
Хорошо видно, что искомые значения y_n находятся последовательно:

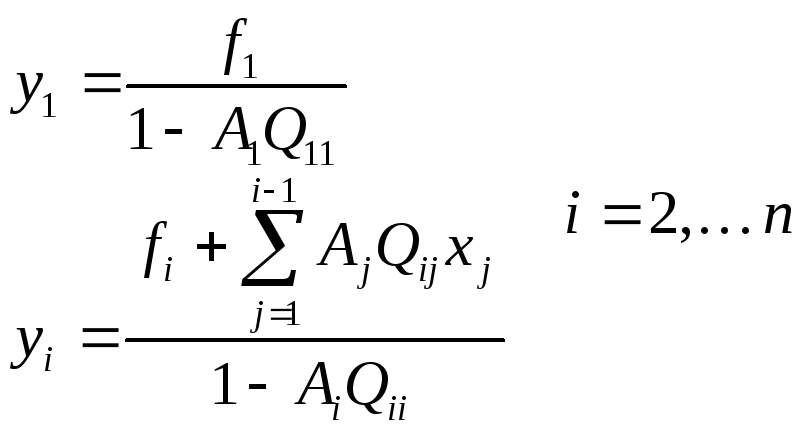
Пример решения уравнения Вольтерры в Mathcad:

7

стр. из 7