32 ГЛАВА 1. СОБЫТИЯ И ВЕРОЯТНОСТЬ
Или, другим способом — c помощью формулы классической
вероятности (1.2): n = C5 |
, |
m = C5 и |
|
||||
|
|
|
|
50 |
|
40 |
|
P (A) = |
m |
= |
C405 |
= |
40 · 39 · 38 · 37 · 36 |
= 0.31 |
|
|
C505 |
50 · 49 · 48 · 47 · 46 |
|||||
|
n |
|
|
|
|
||
Задача. 1.3.8 Вероятности того, что нужная сборщику деталь находится в I, II, III, IV ящике, соответственно равны 0.6; 0.7; 0.8; 0.9. Найти вероятность того, что сборщику придется проверить все 4 ящика (событие A).
Решение. Пусть Ai — {НУЖНАЯ СБОРЩИКУ ДЕТАЛЬ НАХОДИТ-
СЯ В i-м ЯЩИКЕ.}
Тогда
P (A1) |
= |
0.6; P (A1) = 0.4; |
||
|
|
|
|
|
P (A2) |
= |
0.7; P (A2) = 0.3; |
||
P (A3) |
= |
0.8; P (A3) = 0.2; |
||
|
|
|
|
|
P (A4) |
= |
0.1; P (A4) = 0.9. |
||
Имеем :
A = A1A2A3A4 + A1A2A3A4.
Так как события несовместны и независимы, то
P (A) = P (A1A2A3A4 + A1A2A3A4) =
=P (A1A2A3A4) + P (A1A2A3A4) =
=P (A1)P (A2)P (A3)P (A4)+
+P (A1)P (A2)P (A3)P (A4) =
=0.40.30.2(0.9 + 0.1) = 0.024.
1.3.4Задачи для самостоятельного решения
Задача. 1.3.1 Оператор обслуживает три прибора, работающих независимо друг от друга. Известны вероятности того, что в течение часа приборы потребуют внимания оператора: первый — 0.1; второй — 0.25; третий — 0.3. Найти вероятность того, что в течение часа не более одного прибора потребуют внимания оператора.
1.3. СЛОЖЕНИЕ И УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ |
33 |
Ответ: P = 0.885.
Задача. 1.3.2 Известно, что в апреле бывает в среднем 16 солнечных дней. Найти вероятность того, что первого и второго апреля будет различная погода.
Ответ: P = 0.515.
Задача. 1.3.3 Радист вызывает корреспондента. Вероятность того, что вызов будет принят, равна 0.6. Найти вероятность того, что корреспондент ответит лишь на четвертый вызов.
Ответ: P = 0.0384.
Задача. 1.3.4 При каждом включении стартера двигатель начинает работать с вероятностью 0.8. Найти вероятность того, что для запуска двигателя нужно не более двух включений.
Ответ: P = 0.96.
Задача. 1.3.5 B НИИ работают 120 человек, из них 70 знают английский язык, 60 — немецкий, 50 — знают оба языка. Найти вероятность того, что наудачу выбранный сотрудник не знает ни одного иностранного языка.
Ответ: P = 1/3.
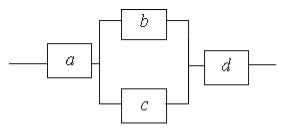
Задача. 1.3.6 Цепь состоит из независимых блоков, соединенных в систему
Зная, что надежность блоков соответственно равна 0.6 для a, 0.7 — для b, 0.8 – для c, 0.9 — для d, найти надежность системы.
Ответ: 0.5076