Задача с. Расчеты на прочность и жесткость прямолинейной стальной балки при плоском изгибе.

1. Применительно к заданной серии балок необходимо:

1.1 Для балок 1÷4 построить эпюры поперечных сил и изгибающих моментов, возникающих в поперечных сечениях.

1.2 Для балки 5, по заданной эпюре изгибающих моментов, используя дифференциальные зависимости между силовыми факторами, построить эпюру поперечных сил и установить характер и величины нагрузок, приложенных к балке (М, Р, q).

Ординаты эпюры моментов αql2, βql2, γql2 подсчитать по исходным данным. (q≠q из исходных данных) На некоторых участках балок эпюры изгибающих моментов изменяются по закону квадратичной параболы. Точкой К отмечена вершина параболы. В сечениях А и В балка 5 шарнирно закреплена. Считать, что распределенные внешние моменты отсутствуют, есть только сосредоточенные моменты.

2. Для балки 2 требуется:

2.1 Подобрать двутавровое сечение, исходя из условия прочности по допускаемым напряжениям, если [σ]=160 МПа. Построить эпюру распределения нормальных напряжений по высоте сечения, рассчитав σ_max и σ в точке перехода из полки в стенку.

2.2 Подобранное сечение проверить на прочность по касательным напряжениям, если [τ]=(0.5÷0.6)[σ]. Построить эпюру распределения касательных напряжений по высоте сечения, рассчитав τ во всех характерных точках.

2.3 Пользуясь соотношением и учитывая расположение опор, изобразить вид изогнутой оси балки.

2.4 Определить грузоподъемность балки из расчета на прочность по допускаемым нагрузкам, предполагая принципиальные изменения заданных внешних нагрузок (пункт для УИРС).

3. Для балки 1, изготовленной из хрупкого материала, имеющего различное сопротивление растяжению и сжатию, расположить наиболее целесообразно сечение, форму и размеры которого взять согласно варианту работы предварительно определив его геометрические характеристики и определив допускаемое значение интенсивности распределенной нагрузки q, считая, что материал балки имеет [σ_раст]=90 МПа и [σ_сж]=350 МПа.

Данные: М = 18 кН·м; Р = 40 кН; q = 48 кН/м; α = 2; β = 5; γ = 1; l = 1 м; m = 0,4 м; k = 0,8 м; р = 0,5 м; серия № 6;

для п.3: h = 7,5 см; α = 0,8; β = 0,75; γ = 0,6; сечение № 10.

Решение.

1. Применительно к заданной серии балок:

   1. строим эпюры поперечных сил и изгибающих моментов, возникающих в поперечных сечениях.

а) для балки 1:

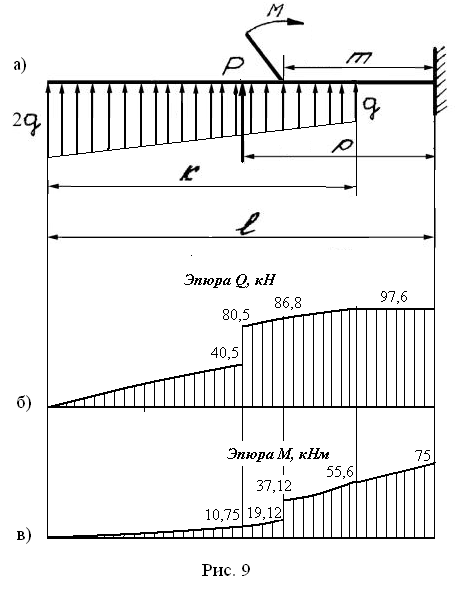
Разобьем консольную балку на 4 участка:

Составляем выражения изгибающих моментов М и поперечных сил Q для каждого участка балки.

Участок I

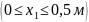
На участке I поперечная сила изменяется по закону квадратичной параболы.

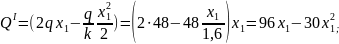
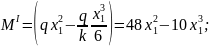
По полученным выражениям вычисляем ординаты эпюр для сечений балки:

при х₁ = 0

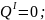
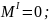
при х₁ = 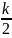= 0,25 м

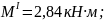
при х₁ = k = 0,5 м

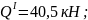
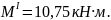
Участок II

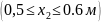
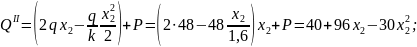
По полученным выражениям вычисляем ординаты эпюр для сечений балки:

при х₂ = 0,5 м

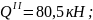
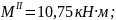
при х₂ = 0,6 м

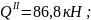
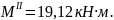
Участок III

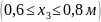
По полученным выражениям вычисляем ординаты эпюр для сечений балки:

при х₃ = 0,6 м

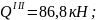
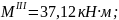
при х₃ = 0,8 м

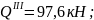
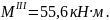
Участок IV

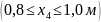
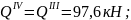
По полученным выражениям вычисляем ординаты эпюр для сечений балки:

при х₄ = 0,8 м

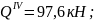
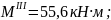
при х₄ = 0,8 м

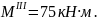
По полученным данным строим эпюру изгибающих моментов М и поперечных сил Q для консольной балки 1 (рис. 9. б,в)

для балки 2

Рис. 10

Составляем расчетную схему балки (рис. 10,а)

Отбрасываем опоры, а их влияние на балку заменяем реакциями R_A и R_B.

Составляем уравнения равновесия балки.

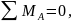
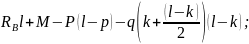(1)

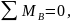
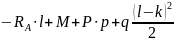. (2)

Из (1) находим

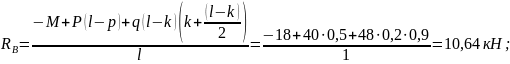
Из (2) находим

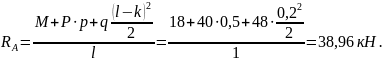
Проверка:

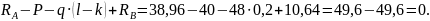
Разобьем балку на 4 участка:

Составляем выражения изгибающих моментов М и поперечных сил Q для каждого участка балки.

Участок I

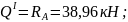
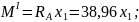
По полученным выражениям вычисляем ординаты эпюр для сечений балки:

при х₁ = 0

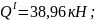
при х₁ = 0,5 м

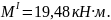
Участок II

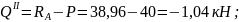
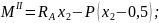
По полученным выражениям вычисляем ординаты эпюр для сечений балки:

при х₂ = 0,5 м

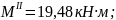
при х₂ = 0,6 м

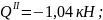
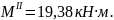
Участок III

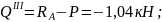
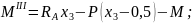
По полученным выражениям вычисляем ординаты эпюр для сечений балки:

при х₃ = 0,6 м

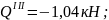
при х₃ = 0,8 м

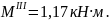
Участок IV

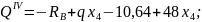
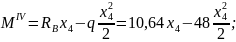
По полученным выражениям вычисляем ординаты эпюр для сечений балки:

при х₄ = 0

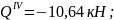
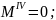
при х₄ = 0,2 м

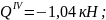
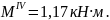
По полученным данным строим эпюру изгибающих моментов М и поперечных сил Q для балки 2 (рис. 10. б,в )

для балки 3

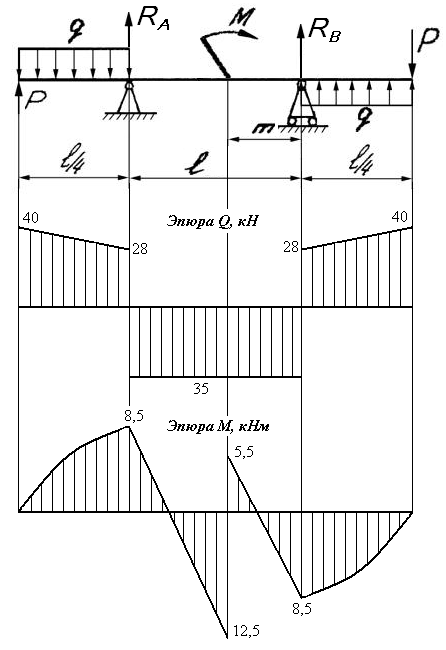
Рис. 10

Составляем расчетную схему балки (рис. 11)

Отбрасываем опоры, а их влияние на балку заменяем реакциями R_A и R_B.

Составляем уравнения равновесия балки.

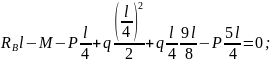(1)

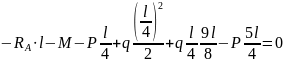. (2)

Из (1) находим

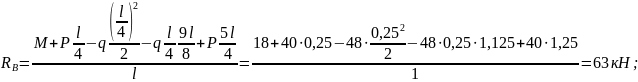
Из (2) находим

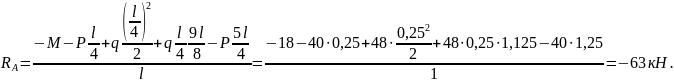
Проверка:

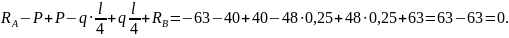
Разобьем балку на 4 участка:

Составляем выражения изгибающих моментов М и поперечных сил Q для каждого участка балки.

Участок I

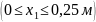
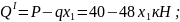
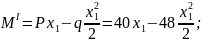
По полученным выражениям вычисляем ординаты эпюр для сечений балки:

при х₁ = 0

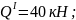
при х₁ = 0,25 м

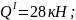
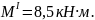
Участок II

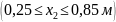
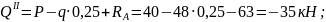
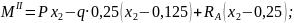
По полученным выражениям вычисляем ординаты эпюр для сечений балки:

при х₂ = 0,25 м

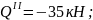
при х₂ = 0,85 м

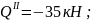
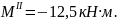
Участок III

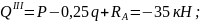
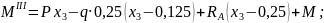
По полученным выражениям вычисляем ординаты эпюр для сечений балки:

при х₃ = 0,85 м

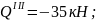
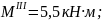
при х₃ = 1,25 м

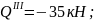
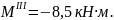
Участок IV

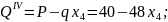
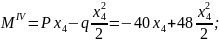
По полученным выражениям вычисляем ординаты эпюр для сечений балки:

при х₄ = 0

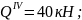
при х₄ = 0,25 м

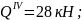
По полученным данным строим эпюру изгибающих моментов М и поперечных сил Q для балки 3 (рис. 11.б,в )

для балки 4

Согласно поэтажной схеме многопролетной балки, построение эпюр

выполняется с балки ВС от заданной нагрузки. Балки АВ и CD нагружаются силами Р_В и Р_С, равным реакциям в опорах В и С, противоположно направленных. Построенные эпюры для трех балок в отдельности объединяются в эпюры внутренних силовых факторов для всей многопролетной балки.

Определим реакции опор R_B и R_C.

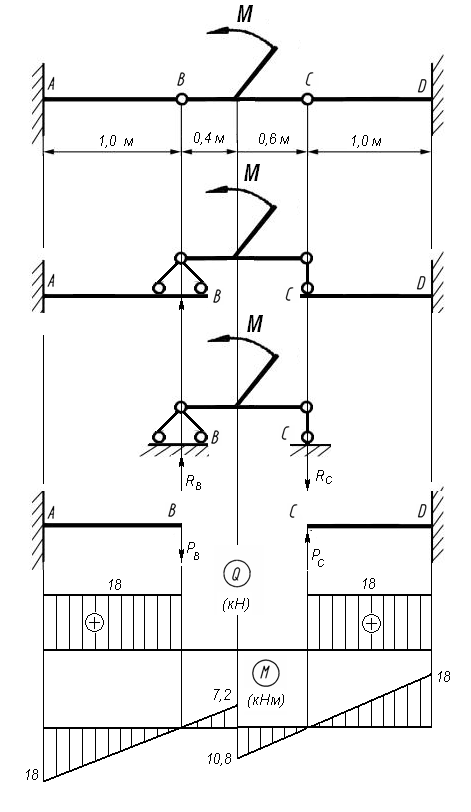
Рис. 12

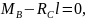отсюда 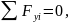отсюда

Эпюра Q и М для балки 4 представлена на рис. 12