2. "Двусвязный список"

• Расскажите о реализации двусвязного списка

Двусвязный спи́сок — структура данных, состоящая из узлов, каждый из которых содержит как собственно данные, так и две ссылки («связки») на следующий и/или предыдущий узел списка.

• Какие структуры для этого требуются?

struct ListNode { int value; struct ListNode *prev; struct ListNode *next; };

struct List { int size; struct ListNode *head; struct ListNode *tail; };

ListNode – данные узла и ссылки на предыдущий и следующий узлы

List – размер, начальный элемент, конечный элемент – для удобства использования операций

• Модифицируйте его для реализации закольцованности.

Разновидностью связных списков является кольцевой (циклический, замкнутый) список. Он тоже может быть односвязным или двусвязным. Последний элемент кольцевого списка содержит указатель на первый, а первый (в случае двусвязного списка) — на последний.

________________________________________________________________________________________

3. Задача сортировки n объектов.

• Базовый алгоритм быстрой сортировки. Его производительность в худшем случае.

1. Выбрать опорный элемент.

2. Сравнить все остальные элементы с опорным, на основании сравнения разбить множество на три — «меньшие опорного», «равные» и «большие», расположить их в порядке меньшие-равные-большие.

3. Повторить рекурсивно для «меньших» и «больших».

В среднем случае сложность алгоритма O(n lg n). В худшем случае сложность алгоритма O(n²).

Худшим случаем, очевидно, будет такой, при котором на каждом этапе массив будет разделяться на вырожденный подмассив из одного опорного элемента и на подмассив из всех остальных элементов. Такое может произойти, если в качестве опорного на каждом этапе будет выбран элемент либо наименьший, либо наибольший из всех обрабатываемых.

В таком случае глубина рекурсии при выполнении алгоритма достигнет n, что будет означать n-кратное сохранение адреса возврата и локальных переменных процедуры разделения массивов. Для больших значений n худший случай может привести к исчерпанию памяти во время работы алгоритма.

• Что такое стабильная сортировка? Какие сортировки стабильны?

Устойчивая (стабильная) сортировка — сортировка, которая не меняет порядок элементов, имеющих одинаковые ключи. Большинство простых методов сортировки устойчивы, большинство сложных — нет.

Стабильные:

1. Сортировка пузырьком O(n2); для каждой пары индексов производится обмен, если элементы расположены не по порядку.

2. Сортировка вставками O(n2); Определяем, где текущий элемент должен находиться в упорядоченном списке, и вставляем его туда

3. Сортировка слиянием O(n log n); требуется O(n) дополнительной памяти; выстраиваем первую и вторую половину списка отдельно, а затем — сливаем упорядоченные списки

• Назовите стандартные реализации сортировок в языке.

Merge, heap, bubble, insertion, quick, shell, selection sorts

• Предложите алгоритм нахождения k-й порядковой статистики, основанный на идее алгоритма Quick Sort. Напишите иллюстрирующий код.

k-ой порядковой статистикой набора элементов линейно упорядоченного множества называется такой его элемент, который является k-ым элементом набора в порядке сортировки.

При реализации вместо рекурсивных вызовов изменяются границы поиска статистики во внешнем цикле. В коде счититаем, что процедура partition принимает массив и границы отрезка, который будет рассечён возвращает индекс опорного элемента.

int findOrderStatistic(int[] array, int k) { int left = 0, right = array.length; while (true) { int mid = partition(array, left, right); if (mid == k) array[mid]; else if (k < mid) right = mid; else { k -= mid + 1; left = mid + 1; } } }

• Оцените среднее и худшее время работы этого алгоритма.

В лучшем случае O(n). В худшем случае O(n^2)

_______________________________________________________________________________

4. Heap Sort

• На основе какой структуры данных реализуется данный алгоритм?

На основе двоичной кучи: Двои́чная ку́ча — такое двоичное дерево, для которого выполнены три условия:

1. Значение в любой вершине не меньше, чем значения её потомков.

2. Каждый лист имеет расстояние до корня либо d либо d-1. Иными словами, если назвать слоем совокупность вершин, находящихся на определённой глубине, то все слои, кроме, быть может, последнего, заполнены полностью.

3. Последний слой заполняется слева направо.

Удобная структура данных для сортирующего дерева — такой массив Array, что: Array[1] — элемент в корне Потомки элемента Array[i] — Array[2i] и Array[2i+1].

• Расскажите сам алгоритм.

1. Выстраиваем элементы массива в виде сортирующего дерева: Array[i]>=Array[2i], Array[2i+1] при 1<=i<=n/2 Этот шаг требует O(n) операций.

2. Будем удалять элементы из корня по одному за раз и перестраивать дерево. То есть на первом шаге обмениваем Array[1] и Array[n], преобразовываем Array[1], Array[2], … , Array[n-1] в сортирующее дерево. Затем переставляем Array[1] и Array[n-1], преобразовываем Array[1], Array[2], … , Array[n-2] в сортирующее дерево. Процесс продолжается до тех пор, пока в сортирующем дереве не останется один элемент. Тогда Array[1], Array[2], … , Array[n] — упорядоченная последовательность. Этот шаг требует O(nlogn) операций.

• Какова сложность алгоритма в среднем? А в худшем случае?

Сложность алгоритма – n log n в худшем случае. В лучшем случае ?

• Напишите код для бинарного поиска.

int binsearch(int *a, int v, int l, int h) { int mid; if (h<l) return -1; mid=(l+h)/2; if (a[mid]>v) return binsearch(a, v, l, mid-1); else if (a[mid]<v) return binsearch(a, v, mid+1, h); else return mid; }

________________________________________________________________________________________

5. Binary Search Tree

• Что такое граф, дерево?

Граф — это совокупность узлов и ребер, соединяющих эти узлы. Дерево — структура данных, эмулирующая древовидную структуру в виде набора связанных узлов. Является связанным графом, не содержащим циклы.

• Что такое бинарное дерево?

Двои́чная ку́ча или сортиру́ющее де́рево — такое двоичное дерево, для которого выполнены три условия:

1. Значение в любой вершине не меньше, чем значения её потомков.

2. Каждый лист имеет глубину либо d либо d-1. Иными словами, если назвать слоем совокупность вершин, находящихся на определённой глубине, то все слои, кроме, быть может, последнего, заполнены полностью.

3. Последний слой заполняется слева направо.

• Опишите Binary Search Tree. В чем его отличие от кучи?

Двоичное дерево поиска — это двоичное дерево, для которого выполняются следующие свойства:

1. О 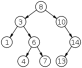ба поддерева — левое и правое, являются двоичными деревьями поиска.

2. У всех узлов левого поддерева произвольного узла X значения ключей меньше, нежели значение ключа узла X.

3. У всех узлов правого поддерева произвольного узла X значения ключей больше, нежели значение ключа узла X.

• Как его можно реализовать?

struct TreeNode { ElementType Element; SearchTree Left; SearchTree Right; };

SearchTree Insert( ElementType X, SearchTree T ) { if( T == NULL ) { T = malloc( sizeof( struct TreeNode ) ); if( T == NULL ) FatalError( "Out of space!!!" ); else { T->Element = X; T->Left = T->Right = NULL; } } else if( X < T->Element ) T->Left = Insert( X, T->Left ); else if( X > T->Element ) T->Right = Insert( X, T->Right ); return T; }

________________________________________________________________________________________