4.3.2Особенности квантования

Величина , или , или существенно влияет на точность восстановления сигнала, представленного в дискретной форме.

Восстановление — это процесс, противоположный процессу преобразования непрерывного сигнала в последовательность чисел.

.

— восстановление.

Пример.

При уменьшении точность восстановления возрастает.

Время дискретизации должно быть меньше наименьшей постоянной времени. Некоторые участки сигнала нельзя восстановить.

Зависимость погрешности восстановления от числа квантований за период выглядит следующим образом:

	5	10	100	300
	0,6	0,3	0,03	0,01

Для синусоиды 300 квантований за период оптимальны.

Таким образом, величина погрешности восстановления определяется количеством дискрет определенного временного промежутка.

1. Представление сигналов в аналоговой и дискретной форме.

2. Уравнения в аналоговой и дискретной форме.

3. Виды передаточных функций в аналоговой и дискретной форме.

Рассмотрим основные положения теории дискретных сигналов.

Существуют следующие методы определения времени, периода, или шага дискретизации:

1. По теореме Котельникова

.

2. Для тиристорного преобразователя:

,

где — число фаз — эта формула для САУ с ТП.

3. Для ШИП (для следящих приводов при контурной обработке):

,

где — скорость обхода контура;

— допустимая погрешность (в пределах 10 микрон);

— радиус тела вращения.

Скорость обхода , где — линейная скорость, мм/мин, около 600 мм/мин. Радиус вращения м.

4. По требуемой точности:

,

где — требуемая точность;

— порядок экстраполяции.

При .

5. По порядку астатизма:

,

где — порядок астатизма.

6. По критерию Джури (по комплексной ПФ).

7. По требуемой точности управления

.

Основные соотношения для дискретных сигналов

1. Сравнительная оценка представления сигналов в САУ

; .

Аналоговая		Дискретная
		,

Примеры представления сигналов приводятся в таблицах преобразования или в таблицах соответствия, которые представлены в математических справочниках.

3. Представление дискретных сигналов в виде решетчатых функций

Решетчатая функция принимает значения в дискретные промежутки времени, а между ними — равна нулю (рис. 98).

Рисунок 98 - Решетчатая функция

3. Представление скорости

,

где — оператор дифференцирования.

Скорость дискретного сигнала

— разность смежных ординат.

3. Уравнение, описывающее уравнение сигналов

Для аналоговых сигналов — дифференциальное уравнение.

Для дискретных сигналов используются разностные уравнения:

.

3. Методы решения уравнений

Для аналоговых сигналов дифференциальные уравнения в операторной форме решаются с применением преобразований по Лапласу:

.

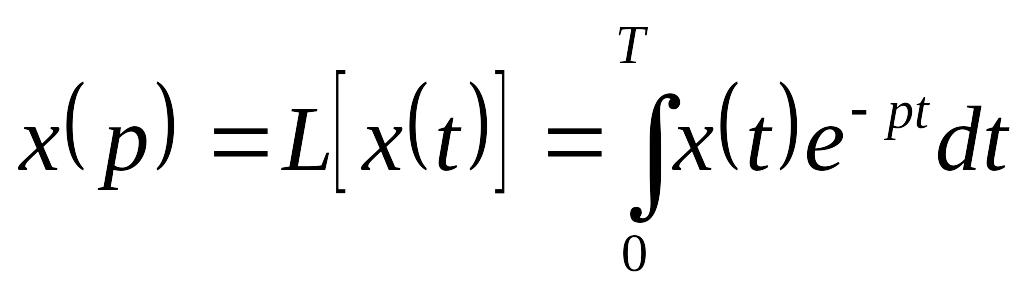Аналоговые системы можно интегрировать, а дискретные — суммировать.

Дискретное преобразование в различных источниках выглядит по-разному.

,

,

,

где — дельта-функция.

3. Передаточные функции при z-преобразованиях

.

Для последовательного соединения

.

Для замкнутой системы

,

.

Передаточная функция для ошибки

.

Для дискретной системы

,

,

и т. д.