Глава III. Статистика равновесных носителей заряда в полупроводниках.

§1. Функция плотности состояний для электронов и дырок в полупроводниках.

Носителями заряда (тока) называют электроны зоны проводимости и дырки валентной зоны. В общем случае в полупроводнике могут содержаться примеси как донорного, так и акцепторного типов. В этом случае приT > 0 K⁰в результате теплового возбуждения электроны будут переходить в зону проводимости переходы (1, 2) и на акцепторные уровни переходы (3).

В результате тепловых переходов 1, 3, образуются носители заряда. Если бы тепловые переходы были единственными, то концентрация носителей заряда непрерывно возрастала бы со временем. С течением времени концентрация электронов была бы , однако эксперименты дают меньшее значение, это связано с тем, что наряду с тепловым возбуждением одновременно протекает обратный процесс – процесс рекомбинации. Это переходы носителей сверху вниз (переходы 1' – 3'). С течением времениустанавливается динамическое равновесие между процессами. В этом случае количество переходов в единицу времени снизу вверх равно количеству переходов сверху вниз. Носители заряда образованные в результате теплового возбуждения и соответствующие состоянию динамического равновесия называются равновесными носителями заряда.

В равновесном состоянии температура кристалла одинакова во всех его точках. В адиабатическом приближении считается, что тепловое движение кристаллической решетки влияет на вероятность заполнения носителями заряда состояний в зонах, но не на сами состояния. В полупроводниках, как и металлах, вероятность заполнения электроном энергетического уровня с энергией определяется функцией распределения Ферми-Дирака:

(1)

где- уровень химического потенциала. Эта функция распределения применима только к равновесным носителям заряда, что подчеркивается знаком₀. Из (1) следует, что приT = 0 K⁰все уровни с энергиейзаполнены электронами, а приуровни свободны от электронов. ПриT > 0 K⁰“ступенька”в функции распределения размывается и появляется хвост кривой распределения. При любойT > 0 K⁰вероятность заполнения уровня с энергиейсогласно (1) равна ½. Значит, уровень химического потенциала это такой уровень, который с одинаковой вероятностью может быть заполнен электронами и свободен от них.

(2)

(2) функция распределения Ферми-Дирака для дырок. Известно, что объем первой зоны Бриллюэна равен . В зоне Бриллюэна число разрешенных волновых векторовNравно числу элементарных ячеек кристалла. Тогда, на одно разрешенное квантовое состояние будет приходиться объем обратного пространства равный:

где V– объем кристалла. В кристаллах единичного объема на одно разрешенное состояние приходится объем обратного пространства равный. Впредь будем рассматривать кристаллы единичного объема.

Найдем аналогичное выражение для числа состояний в кристаллах единичного объема, которые занимают электроны в интервале энергий отдо. Для определенности будем рассматривать зону проводимости, дно которой лежит в центре зоны Бриллюэна;такую зону имеют кристаллы кубической системыA₂B₆,A₃B₅. Как показано нами, такой экстремум характеризуется одной компонентой эффективной массы, т.е. эффективная масса изотропная величина, изоэнергетическая поверхность такого экстремума – сфера. На поверхности такой сферы лежат концы таких разрешенных волновых векторов, которые одинаковые значения модуля равное.

Очевидно число состояний, которым соответствуют волновые вектора, модули которых имеют значение от до, равно отношению объема шарового слоя толщинойк объемупространства, приходящемуся на одно квантовое состояние:

(3)

Как известно для сферической изоэнергетической поверхности закон дисперсии имеет параболическую форму:

(4)

Из (4) следует, что

,,

(5)

Подставим (5) в (3) и получим:

(6)

(6) определяет собой число квантовых состояний в кристалле единичного объема, которые занимают электроны с энергией в интервале от до.

(7)

(7) – функция плотности состояний для электронов зоны проводимости. Она определяет собой число состояний в кристалле единичного объема приходящегося на единичный интервал энергии вблизи энергии . Видно, что плотность состояний возрастает с энергией электронов, она выше в кристаллах с большей эффективной массой электронов. Видно, что она не зависит от температуры.

Для дырок валентной зоны функция распределения равна:

(8)

На рисунке площадь заштрихованного прямоугольника равна:

и численно равна числу электронных состояний в интервале энергий .

На зависимости функции плотности состояний от эффективной массы основан эффект Бурштейна-Масса. Он состоит в смещении края оптического поглощения в фиолетовую область спектра по мере легирования кристалла мелкими примесями.

Для примера рассмотрим два кристалла, которые имеют одинаковые характеристики, но разные эффективные массы электронов.

П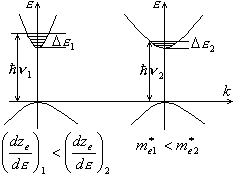о мере легирования будет возрастать число электронов в зоне проводимости, при данных уровнях легирования интервал энергии, которые занимают электроны в зоне проводимости будет больше у первого кристалла. Из диаграммы видно, что для межзонных оптических переходов, нужна энергия оптических квантов. Для того, чтобы наблюдать эффект Бурштейна-Масса необходимо выбирать полупроводники с малыми эффективными массами.

У непрямозонных полупроводников:германий, кремний, дно зоны проводимости лежит не в центре зоны Бриллюэна. В общем случае такие экстремумы характеризуются тремя компонентами эффективной массы:. В этом случае выражение для функции плотности имеет вид:

(9)

где- эффективная масса плотности состояний,M– число полных эллипсоидов (долин),M_Si = 6, M_Ge = 4. УGeэкстремум зоны проводимости лежит на границе зоны Бриллюэна в точкахLна линии [111]. Так как точкиLлежат на границе зоны Бриллюэна, то на нее приходится 8 полудолин, т.е. 4 полных долины.