§8. Ударная ионизация в полупроводниках.

В отсутствии внешнего электрического поля или в слабых полях зоны полупроводников в координатах являются горизонтальными, это означает, что для электрона в любой точке кристалла нужна одинаковая энергия, чтобы попасть, например, на дно зоны проводимости (смотри рисунок).

Вэлектрических поляхзоны полупроводников“наклоняются”. Это является результатом того, что потенциальная энергия электрона в присутствии внешнего электрического поля зависит от координатыx, если внешнее поле имеет направление как показано на рисунке, то потенциальная энергия электронов с ростомxвозрастает по закону, наклон определяется величиной. Внешнее полезначительно меньше внутренних кристаллических полей, следовательно, они не изменяют такие фундаментальные параметры кристалла;как ширина запрещенной зоны, энергия ионизация примесей.

В связи с этим потолок валентной зоны, примесные уровни и дно зоны проводимости наклоняются, т.е. в этом случае ,.

Для определенности будем рассматривать полупроводник донорного типа. Под действием электрического поля свободные электроны ускоряются в направлении противоположному полю . На длине свободного пробегаэти электроны приобретают от поля энергию, которая затрачивается на кинетическую энергию, на путипотенциальная энергия уменьшается на эту же величину, следовательно, полная энергия электрона в электрическом поле равна: (на диаграмме горизонтальная линия). Энергия разогретых электрическим полем электронов может стать такой, что она достаточна для ионизации за счет соударений доноров(I) или основных атомов кристалла (II), при этом сам свободный электрон после соударения остается в зоне проводимости. В результате соударений (I) в зоне проводимости появляется вместо одного два свободных электрона, они ускоряются электрическим полем и эти два электрона могут произвести ионизацию двух доноров, в результате этого ток через полупроводник будет резко возрастать. В очень сильных электрических полях энергия разогретых электронов может быть достаточна для ионизации основных атомов кристалла. В результате такого акта (II) появляется свободный электрон, свободная дырка и сам ионизирующий электрон при большой энергии может остаться в зоне проводимости, ускоряются электрическим полем и могут произвести акт (II). В этом случае будет иметь место еще более резкое возрастание тока с напряженностью электрического поля. Акты соударения разогретых носителей заряда с примесными или основными атомами кристалла называются ударной ионизацией.

Эффект ударной ионизации наиболее ярко выражен в полупроводниках, в которых носители заряда имеют высокую подвижность при низких температурах кристалла, например: в кристалле Ge эффект ударной ионизации при T = 4,2 K. Наблюдается в электрических полях (смотри рисунок).

§9. Туннельный эффект в полупроводниках (электростатическая ионизация Зинера).

Может наблюдаться в электрических полях . Если энергия электронато классический электрон не может попасть внутрь такого барьера, так как в этом случае кинетическая энергия равна:

импульс – мнимый. Но с квантовой точки зрения электрон с такими энергетическими параметрами может просочиться сквозь потенциальный барьер, проходя его без изменения своей энергии (туннельный эффект). Туннельный эффект может быть объяснен соотношением неопределенности:

Фиксация электрона внутри барьера приводит к неопределенности импульса электрона и его кинетической энергии:

,

Очевидно, туннельное просачивание возможно, если неопределенность кинетической энергии равна:

Туннельный эффект характеризуется коэффициентом прозрачности барьера Д, он равен отношению числа частиц прошедших сквозь барьер к числу частиц падающих на барьер. Для барьера прямоугольной формы:

В сильных электрических полях (крутой наклон зон) возможны туннельные переходы электронов с донорных центров в зону проводимости или из валентной зоны в зону проводимости. Рассмотрим туннельный эффект электронов из валентной зоны в зону проводимости. Такой электрон туннелирует сквозь потенциальный барьер треугольной формы.

Будем рассматривать туннелирование валентного электрона, имеющего энергию . Он туннелирует из точкиO в точку L. Потенциальный барьер OAL имеет треугольную форму, Высота его U. Аппроксимируем этот треугольный барьер суммой узких прямоугольных барьеров. Например, для i барьера, ширина которого dx, коэффициент прозрачности будет:

Высота i барьера .,ширина треугольного барьера. Очевидно, коэффициент треугольного барьера равен:

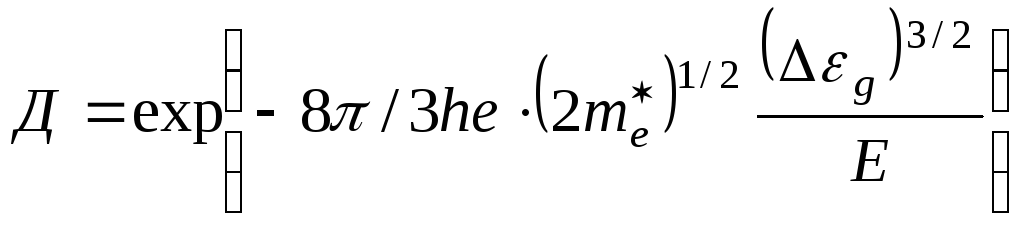(1)

Из (1) следует, что вероятность туннельного просачивания электронов из валентной зоны в зону проводимости экспоненциально возрастает с напряженностью электрического поля и тем быстрее, чем меньшеи. Расчеты показывают, что приимежзонное туннелирование начинается при. При меньших электрических полях возможно туннелирование электронов с донорных уровней через треугольный барьер. В этом случае коэффициент прозрачности будет равен:

С квантовой точки зрения туннелирование возможно при условии, когда длина электронной волны соизмерима с шириной потенциального барьера. А ширину потенциального барьера можно варьировать величиной электрического поля (чем больше поле, тем меньше ширина потенциального барьера: ).