§13. Топз в полупроводниках с ловушками.

В кристаллических полупроводниках возможно существование одиночных (дискретных) уровней ловушек. В аморфных, стеклообразных и поликристаллических материалах вероятнее существование распределенной плотности уровней ловушек, связанной с разоупорядочением решеток. Ловушки захватывают инжектированные из омического контакта носители заряда, создавая пространственный заряд, ограничивающий ток через высокомные пленки (ловушечный ТОПЗ). Поведение ВАХ в этом случае определяется характером распределения ловушек по энергиям.

1. ТОПЗ в полупроводниках с мелкими дискретными ловушками.

Пусть в диэлектрике или высокоомном полупроводнике имеются мелкие ловушки донорного типа, для которых выполняется соотношение:

- энергия ловушки.

О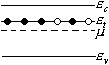но имеет место тогда, когда инжекция носителей заряда недостаточно эффективна (среднее электрическое поле), т.е. в этом случае концентрация инжектированных зарядов меньше, чем концентрация ловушечных центров. Найдем отношение концентрации свободных и захваченных ловушками электронов:

- концентрация ловушек, - вероятность заполнения ловушек.

Чтобы получить выражение для ВАХ ловушечного ТОПЗ, необходимо умножить выражение для безловушечного ТОПЗ на величину :

- подвижность.

Т.е. и в этом случае имеет место квадратичная зависимость тока от напряжения, но в отличии от безловушечного ТОПЗ, ток в этом случае будет сильно зависеть от температуры. Снимая зависимость ВАХ при различных температурах, можно определить энергию ионизации ловушек. Действительно, от температуры зависят: ,. Выберем значение токов при фиксированном значении, тогда перестроим токовую зависимость в координатахии из тангенса наклона этой зависимости можно определить.

, ,

,

Сростом напряжениярастет концентрация инжектированных носителей заряда и следовательно степень заполнения электронами ловушек. Наконец, при некотором значении напряженияможет наступить полное заполнение ловушек, в связи с этим ток через материал резко возрастает и при дальнейшем повышении напряжения ток подчиняется квадратичному закону. Напряжение полного заполнения ловушексвязано с параметрами образца соотношениями:

- толщина образца, - диэлектрическая проницаемость. Из этого соотношения можно определить концентрацию ловушек.

1 – омический участок ВАХ (2 параллельна 4).

2 – квадратичный ловушечный ТОПЗ.

3 – ток, соответствующий .

4 – квадратичный безловушечный ТОПЗ.

2. ТОПЗ в полупроводниках с непрерывным распределением ловушек.

Рассмотрим наиболее распространенную ситуацию, когда между зоной проводимости и “темновым” уровнем химического потенциала (положение уровня химического потенциала до инжекции носителей заряда) существует непрерывное равномерное распределение глубоких уровней ловушек.

Пусть в объеме полупроводника из омического контакта инжектируются неравновесные электроны. Так как концентрация ловушек значительно больше концентрации свободных носителей заряда, то с хорошим приближением можно считать, что весь инжектированный заряд находится на захватывающих центрах (смотри рисунок). На рисунке- новый уровень химического потенциала, т.е.после инжекции носителей заряда. Будем рассматривать полупроводник толщинойL и с единичной площадью поперечного сечения. После приложения напряжения концентрация свободных носителей заряда:

(1)

- расстояние между и,- равновесная концентрация носителей заряда.

- число ловушек в единице объема, приходящихся на единичный интервал энергии.

(2)

(3)

, - концентрация носителей заряда, захваченных ловушками.

(4)

Чтобы получить выражение ловушечного ТОПЗ при однократном распределении ловушек по энергиям, необходимо безловушечный ТОПЗ умножить на (4):

(5)

В данном случае ток изменяется по экспоненциальному закону. Из (5) можно рассчитать :

,

3. ТОПЗ в полупроводниках с непрерывным экспоненциальным распределением глубоких ловушек.

экспоненциально убывает с увеличением энергии ионизации ловушек, т.е.

,

- параметр, называемый характеристической температурой и используется для приближенного уравнивания скорости убывания концентрации ловушек с ростом глубины их залегания в запрещенной зоне. Очевидно, если, то

(2 пункт), если - то случай мелких ловушек. При, имеет место следующая ВАХ:

Видно, что ток возрастает по степенному закону от напряжения:

, ,

,

,

,

При ТОПЗ зависит от величиныL по закону:

,

,

,