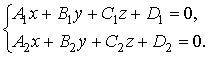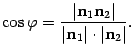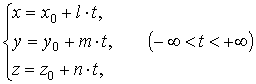- •1. Определители и их свойства.
- •2. Матрицы. Умножение матриц.
- •3. Обратная матрица.
- •Теорема условия существования обратной матрицы
- •Алгоритм нахождения обратной матрицы
- •4. Правило Крамера решения систем линейных уравнений.
- •5. Метод Гаусса решения систем линейных уравнений.
- •6. Системы координат.
- •Операция сложения двух векторов - правило треугольника.
- •8. Скалярное произведение векторов. Длина вектора.
- •11. Уравнение прямой с угловым коэффициентом.
- •12. Расстояние от точки до прямой.
- •13. Уравнение прямой, проходящей через две заданные точки.
- •14. Угол между двумя прямыми на плоскости.
- •15. Условия параллельности и перпендикулярности прямых.
- •16. Уравнения плоскости в пространстве.
- •17. Угол между плоскостями.
- •18. Уравнение прямой в пространстве.
- •19. Угол между прямыми в пространстве.
17. Угол между плоскостями.
Пусть
плоскости
![]() и
и
![]() заданы
соответственно уравнениями
заданы
соответственно уравнениями
![]() и
и
![]() .
Требуется найти угол
.
Требуется найти угол
![]() между
этими плоскостями.
между
этими плоскостями.
Плоскости,
пересекаясь, образуют четыре двугранных
угла (рис. 11.6): два тупых и два острых или
четыре прямых, причем оба тупых угла
равны между собой, и оба острых тоже
равны между собой. Мы всегда будем искать
острый угол. Для определения его величины
возьмем точку
![]() на
линии пересечения плоскостей и в этой
точке в каждой из плоскостей проведем
перпендикуляры
на
линии пересечения плоскостей и в этой
точке в каждой из плоскостей проведем
перпендикуляры
![]() и
и
![]() к
линии пересечения. Нарисуем также
нормальные векторы
к
линии пересечения. Нарисуем также
нормальные векторы
![]() и
и
![]() плоскостей
и
с
началами в точке
(рис.
11.6).
плоскостей
и
с
началами в точке
(рис.
11.6).

Рис.11.6.Угол между плоскостями
Если
через точку
провести
плоскость
![]() ,
перпендикулярную линии пересечения
плоскостей
и
,
то прямые
и
и
изображения векторов
и
будут
лежать в этой плоскости. Сделаем чертеж
в плоскости
(возможны
два варианта: рис. 11.7 и 11.8).
,
перпендикулярную линии пересечения
плоскостей
и
,
то прямые
и
и
изображения векторов
и
будут
лежать в этой плоскости. Сделаем чертеж
в плоскости
(возможны
два варианта: рис. 11.7 и 11.8).

Рис.11.7.Угол между нормальными векторами острый

Рис.11.8.Угол между нормальными векторами тупой
В
одном варианте (рис. 11.7)
![]() и
и
![]() ,
следовательно, угол
,
следовательно, угол
![]() между
нормальными векторами равен углу
,
являющемуся линейным углом острого
двугранного угла между плоскостями
и
.
между
нормальными векторами равен углу
,
являющемуся линейным углом острого
двугранного угла между плоскостями
и
.
Во
втором варианте (рис. 11.8)
![]() ,
а угол
между
нормальными векторами равен
,
а угол
между
нормальными векторами равен
![]() .
Так как
.
Так как
![]()
то
в обоих случаях
![]() .
.
По
определению скалярного произведения
![]() .
Откуда
.
Откуда
![]()
и соответственно
|
(11.4) |
Так как координаты нормальных векторов известны, если заданы уравнения плоскостей, то полученная формула (11.4) позволяет найти косинус острого угла между плоскостями.
Если плоскости перпендикулярны, то перпендикулярны и их нормальные векторы. Получаем условие перпендикулярности плоскостей:
|
(11.5) |
Если плоскости параллельны, то коллинеарны их нормальные векторы. Получаем условие параллельности плоскостей
|
18. Уравнение прямой в пространстве.
Пусть дана точка М0(х0, у0, z) (опорная точка прямой) и направляющий вектор р (l, m, n). Составить в векторном виде уравнение прямой линии, проходящей через точку М0 в направлении вектора р. Пусть М (х, у, z) - текущая точка прямой. Тогда векторы M0M и p коллинеарны. По условию коллинеарности векторов можно записать
|
, (- ∞ < t < + ∞) |
(13.1) |
и представить соотношение (13.1) в виде
|
, (- ∞ < t < + ∞) |
(13.2) |
Уравнение (13.2) является уравнением прямой линии в векторном параметрическом виде.
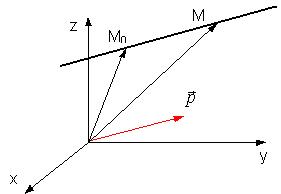
Параметрическое уравнение прямой линии
Векторное уравнение (13.2) в координатной форме представляется следующим образом
|
(13.3) |
Каноническое уравнение прямой линии в пространстве
Исключив t из уравнения (13.3), разрешив их сначала относи-тельно t, а затем, приравняв правые части равенств, имеем:
|
(13.4) |
Если какая – либо координата направляющего вектора равна нулю, то равен нулю и числитель дроби.
Уравнение прямой линии в пространстве, проходящей через две заданные точки
Пусть заданы две точки М1(х1, у1, z1) и М2(х2, у2, z2), через которые должна проходить прямая линия. Примем за направляющий вектор прямой вектор
![]() .
.
Поэтому уравнение (13.4) примет вид
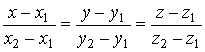 .
.
Общее уравнение прямой линии в пространстве
Прямая в пространстве может быть задана также как пересечение двух плоскостей, если плоскости не параллельны: