
- •1. Определители и их свойства.
- •2. Матрицы. Умножение матриц.
- •3. Обратная матрица.
- •Теорема условия существования обратной матрицы
- •Алгоритм нахождения обратной матрицы
- •4. Правило Крамера решения систем линейных уравнений.
- •5. Метод Гаусса решения систем линейных уравнений.
- •6. Системы координат.
- •Операция сложения двух векторов - правило треугольника.
- •8. Скалярное произведение векторов. Длина вектора.
- •11. Уравнение прямой с угловым коэффициентом.
- •12. Расстояние от точки до прямой.
- •13. Уравнение прямой, проходящей через две заданные точки.
- •14. Угол между двумя прямыми на плоскости.
- •15. Условия параллельности и перпендикулярности прямых.
- •16. Уравнения плоскости в пространстве.
- •17. Угол между плоскостями.
- •18. Уравнение прямой в пространстве.
- •19. Угол между прямыми в пространстве.
Теорема условия существования обратной матрицы
Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.
Матрица А = (А1,
А2,...Аn)
называется невырожденной,
если векторы-столбцы являются линейно
независимыми. Число линейно независимых
векторов-столбцов матрицы называется
рангом матрицы
![]() .
Поэтому можно сказать, что для того,
чтобы существовала обратная матрица,
необходимо и достаточно, чтобы ранг
матрицы равнялся ее размерности, т.е. r
= n.
.
Поэтому можно сказать, что для того,
чтобы существовала обратная матрица,
необходимо и достаточно, чтобы ранг
матрицы равнялся ее размерности, т.е. r
= n.
Алгоритм нахождения обратной матрицы
Записать в таблицу для решения систем уравнений методом Гаусса матрицу А и справа (на место правых частей уравнений) приписать к ней матрицу Е.
Используя преобразования Жордана, привести матрицу А к матрице, состоящей из единичных столбцов; при этом необходимо одновременно преобразовать матрицу Е.
Если необходимо, то переставить строки (уравнения) последней таблицы так, чтобы под матрицей А исходной таблицы получилась единичная матрица Е.
Записать обратную матрицу А-1, которая находится в последней таблице под матрицей Е исходной таблицы.
Пример 1
Для матрицы А найти обратную матрицу А-1
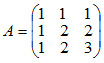
Решение: Записываем матрицу А и справа приписываем единичную матрицу Е. Используя преобразования Жордана, приводим матрицу А к единичной матрице Е. Вычисления приведены в таблице 31.1.
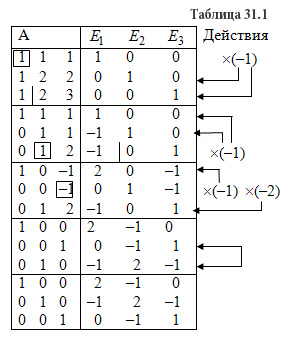
Проверим правильность вычислений умножением исходной матрицы А и обратной матрицы А-1.
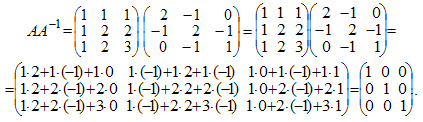
В результате умножения матриц получилась единичная матрица. Следовательно, вычисления произведены правильно.
Ответ:

4. Правило Крамера решения систем линейных уравнений.
Метод Крамера состоит в том, что мы последовательно находим главный определитель системы (5.3), т.е. определитель матрицы А
D = det (ai j)
и n вспомогательных определителей D i (i= ), которые получаются из определителя D заменой i-го столбца столбцом свободных членов.
Формулы Крамера имеют вид:
D × x i = D i ( i = ). (5.4)
Из (5.4) следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы (5.3): если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам:
x i = D i / D.
Если главный определитель системы D и все вспомогательные определители D i = 0 (i= ), то система имеет бесчисленное множество решений. Если главный определитель системы D = 0, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.
5. Метод Гаусса решения систем линейных уравнений.
Алгоритм решения систем уравнений методом Жордана-Гаусса состоит из ряда однотипных шагов, на каждом из которых производятся действия в следующем порядке:
Проверяется, не является ли система несовместной. Если система содержит противоречивое уравнение, то она несовместна.
Проверяется возможность сокращения числа уравнений. Если в системе содержится тривиальное уравнение, его вычеркивают.
Если система уравнений является разрешенной, то записывают общее решение системы и если необходимо — частные решения.
Если система не является разрешенной, то в уравнении, не содержащем разрешенной неизвестной, выбирают разрешающий элемент и производят преобразование Жордана с этим элементом.
Далее заново переходят к пункту 1
Пример 3 Решить систему уравнений методом Жордана-Гаусса.
Найти: два общих и два соответствующих базисных решения
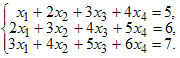
Решение:
Вычисления приведены в нижеследующей таблице:
Справа от таблицы изображены действия над уравнениями. Стрелками показано к какому уравнению прибавляется уравнение с разрешающим элементом, умноженное на подходящий множитель.
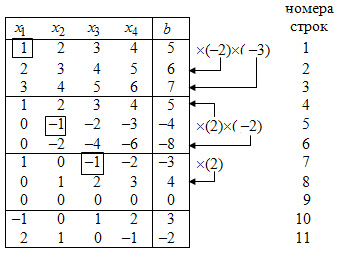
В первых трех строках таблицы помещены коэффициенты при неизвестных и правые части исходной системы. Результаты первого преобразования Жордана с разрешающим элементом равным единице приведены в строках 4, 5, 6. Результаты второго преобразования Жордана с разрешающим элементом равным (-1) приведены в строках 7, 8, 9. Так как третье уравнение является тривиальным, то его можно не учитывать.
Равносильная
система с
разрешенными неизвестными
![]() и
и
![]() имеет
вид:
имеет
вид:
![]()
Теперь можем записать Общее решение:
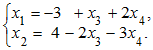
Приравниваем
свободные переменные
![]() и
и
![]() нулю
и получаем:
нулю
и получаем:
![]() .
.
Базисное
решение:
![]()
Для
того чтобы найти второе общее и
соответствующее ему базисное решение,
в полученной разрешенной системе в
каком-либо уравнении необходимо выбрать
какой-либо другой разрешающий элемент.
(дело в том, что линейное уравнение может
содержать несколько общих и базисных
решений). Если разрешенная система
уравнений, равносильная исходной системе
содержит
![]() неизвестных
и
неизвестных
и
![]() уравнений,
то число общих и соответствующих базисных
решений исходной системы равно числу
сочетаний
и
.
Количество сочетаний можно вычислить
по формуле:
уравнений,
то число общих и соответствующих базисных
решений исходной системы равно числу
сочетаний
и
.
Количество сочетаний можно вычислить
по формуле:
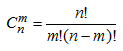
В нашем случае выбран разрешающий элемент (-1) в первом уравнении при (строка 7). Далее производим преобразование Жордана. Получаем новую разрешенную систему (строки 10,11) c новыми разрешенными неизвестными и :
![]()
Записываем второе общее решение:
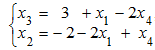
И
соответствующее ему базисное
решение:
![]()
Ответы:
Общее решение:
Базисное решение:
Общее решение:
Базисное решение:
