2. Матрицы. Умножение матриц.

Прямоугольной матрицей размера mxn называется совокупность mn чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов. Мы будем записывать матрицу в виде

                                                                 (4.1)

или сокращенно в виде A = (a_{i j}) (i = ; j = ). Числа a_{i j}, составляющие данную матрицу, называются ее элементами; первый индекс указывает на номер строки, второй - на номер столбца. Две матрицы A = (a_{i j}) и B = (b_{i j}) одинакового размера называются равными, если попарно равны их элементы, стоящие на одинаковых местах, то есть A = B, если a_{i j} = b_{i j}.

Матрица, состоящая из одной строки или одного столбца, называется соответственно вектор-строкой или вектор-столбцом. Вектор-столбцы и вектор-строки называют просто векторами.

Матрица, состоящая из одного числа, отождествляется с этим числом. Матрица размера mxn, все элементы которой равны нулю, называются нулевой матрицей и обозначается через 0. Элементы матрицы с одинаковыми индексами называют элементами главной диагонали. Если число строк матрицы равно числу столбцов, то есть m = n, то матрицу называют квадратной порядка n. Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональными матрицами и записываются так:

.

Если все элементы a_{i i} диагональной матрицы равны 1, то матрица называется единичной и обозначается буквой Е:

                                                                          .

Квадратная матрица называется треугольной, если все элементы, стоящие выше (или ниже) главной диагонали, равны нулю. Транспонированием называется такое преобразование матрицы, при котором строки и столбцы меняются местами с сохранением их номеров. Обозначается транспонирование значком Т наверху.

Пусть дана матрица (4.1). Переставим строки со столбцами. Получим матрицу

,

которая будет транспонированной по отношению к матрице А. В частности, при транспонировании вектора-столбца получается вектор-строка и наоборот.

Произведением матрицы А на число l называется матрица, элементы которой получаются из соответствующих элементов матрицы А умножением на число l: l A = (l a_{i j}).

Суммой двух матриц А = (a_{i j}) и B = (b_{i j}) одного размера называется матрица C = (c_{i j}) того же размера, элементы которой определяются по формуле c_{i j} = a_{i j} + b_{i j}.

Произведение АВ матрицы А на матрицу В определяется в предположении, что число столбцов матрицы А равно числу строк матрицы В.

Произведением двух матриц А = (a_{i j}) и B = (b_{j k}), где i = , j= , k= , заданных в определенном порядке АВ, называется матрица С = (c _{i k}), элементы которой определяются по следующему правилу:

c _{i k} = a_{i 1} b_{1 k} + a_{i 2} b_{2 k} +... + a_{i m} b_{m k} = a_{i s} b_{s k}.                    (4.2)

Иначе говоря, элементы матрицы-произведения определяются следующим образом: элемент i-й строки и k-го столбца матрицы С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-го столбца матрицы В.

3. Обратная матрица.

Пусть имеется квадратная матрица n-го порядка

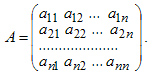
Матрица А^-1 называется обратной матрицей по отношению к матрице А, если А*А^-1 = Е, где Е — единичная матрица n-го порядка.

Единичная матрица — такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу, — единицы, а остальные — нули, например:

Обратная матрица может существовать только для квадратных матриц т.е. для тех матриц, у которых число строк и столбцов совпадают.