Колмаков Ю.Н. Лекции по физике ТулГУ. Механика / mech-zad-TulGU

Добавил:

Studfiles2 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уфимский Государственный Авиационный Технический Университет

Предмет:

Физика

Файл:

ния связана со скоростью центра масс соотношением ω = vC

.pdf

Скачиваний:

540

Добавлен:

02.05.2014

Размер:

3.32 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 195 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Плоское движение	41
	Плоское движение
	Задача 2.20
Однородный шар массы	m и радиуса R начинает скатываться без

скольжения с наклонной плоскости, составляющей угол α с горизонтом. Найти зависимость от времени момента импульса шара относительно точки касания в начальный момент времени. Как изменится результат в случае абсолютно гладкой поверхности?

Решение

Можно показать ([1], c.130), что момент импульса системы (шара) отно-
сительно точки O :	G	G	G G
	L0 = L +[rC , p],
	G
	где L – собственный момент импульса, обу-
	словленный вращением системы вокруг оси,
	проходящей через центр масс, а [rGC , pG] – мо-
	мент импульса, обусловленный движением
	системы как целого. Из рис.2.29 видно, что
	оба этих вектора в данной задаче перпенди-
	кулярны плоскости чертежа и направлены от
рис. 2.29	нас. Так	как		[rGC , pG]	= mvC rC sin ϕ = mvC R ,

L = Iω, момент инерции шара I = 2mR25 , а угловая скорость его враще-

Запишем теперь уравнения динамики поступательного движения шара в проекции на ось x (рис.2.29) и вращательного движения вокруг оси C :

ma		= mg sin α− F	,
	C	тр
	Iε = F R.
		тр

В отсутствии скольжения угловое ускорение шара ε = aC R и, исключая из

системы уравнений F	, получаем ускорение центра масс a =	g sin α	=
		1+ I mR2
тр	C

= 5g sin α 7 . Движение равноускоренное, поэтому vC = aC t = 5gt sin α7 . Подставляя этот результат вформулу(2.36), получаем искомую зависимость

L0 = mgR sin α t .		(2.37)
При скольжении шара Fтр = 0 , ω = 0 ,	aC = g sin α ,	L0 = mvC R и, по-
прежнему, vC = aC t , т.е. приходим к тому	же результату (2.37).

Решение

На рис.2.31 обозначены все силы, действующие на каждое тело порознь. На начавший скользить куб со стороны плоскости действует сила трения скольжения, определяемая величиной силы реакции: Fтр1 = µN1 . Для катящегося без

42	Глава 2. Динамика.

Задача 2.21

На наклонной плоскости, угол наклона α которой к го-
ризонту можно изменять, лежат, соприкасаясь, однород-
ный куб массы	m	и сплошной цилиндр массы	m
	1		2
(рис.2.30). При увеличении угла α до некоторое критиче-
ского значения куб начинает скользить, а цилиндр –			ка-	рис. 2.30
титься без скольжения. Найти это значениеαкр , полагая,

что коэффициент трения равен одному и тому же значению µ во всех точках соприкосновения тел.

рис. 2.31	скольжения цилиндра Fтр2 < µN2 !
Обозначим через FG	силу взаимодействия тел. Начав вращаться, ци-

линдр скользит по грани куба, действуя на него с силой трения скольже-
ния FG' . Со стороны куба на цилиндр действует противоположно направ-
тр
ленная сила FG'' (рис.2.31). Естественно, что F'		= F'' = µF .
тр	тр	тр
Проекции уравнения поступательного движения куба на оси x и			y об-
разуют систему:
m1a = m1g sin α−µN1	+ F
N1 = m1g cos α+µF	, откуда, исключая реакцию N1 , находим:
N1 = m1g cos α+µF
m1a = m1g sin α+ F (1−µ2 )−µm1g cos α .			(2.38)

Плоское движение цилиндра также определяется уравнениями поступательного движения центра масс (в проекции на оси x и y ) с тем же уско-

рением a . Дополнительно надо записать уравнение вращательного движения с угловым ускорением ε вокруг оси, проходящей через центр масс. Так как момент инерции цилиндра с радиусом R относительно данной

оси I = m2 R2 2 , а при качении без проскальзывания ε = aR , то система уравнений, описывающих движение цилиндра имеет вид:

Гироскопический эффект									43
		m a = m g sin α− F − F					,
		m a = m g sin α− F − F					,
		2			2	тр2
		N2 = m2 g cos α−µF ,							(2.39)
				mR
		Iε =		mR	a = Fтр2

			2			R −µF R.
			2
Вначале исключим из первого и последнего уравнения системы (2.39)
неизвестную силу Fтр2 и получим:
		3m2a 2 = m2 g sin α− F (1+µ).							(2.40)
Затем, исключая из соотношений (2.38) и (2.40) силу F , находим:
m +1,5m		(1−µ) a = m g sin α−µm g cos α+(1−µ)m g sin α .
1	2		1			1		2

Для того, чтобы движение началось, т.е. a ≥ 0 , необходимо выполнение

неравенства:		m		+ m	(1−µ) g sin α−µm g cos α ≥ 0 ,
			1	2				1
или tgα ≥		µm1	,	откуда αкр		= arctg		µm1	(2.41)
или tgα ≥	m1	+m2 (1−µ)	,	откуда αкр		= arctg	m1	+m2 (1−µ)	(2.41)
	m1	+m2 (1−µ)					m1	+m2 (1−µ)

Проверим выполнение условий задачи. Из уравнений (2.39) и (2.40) при a = 0 (α = αкр ) находим:

F = m2 g sin αкр	(1+µ);	Fтр2 = µF;		N2 = ((m1 + m2 )(1−µ2 )		µm1 +1)F .
	Условие		отсутствия		скольжения	цилиндра
	Fтр2 < µN2		дает	(m1 +m2 )(1−µ2 )> 0 и выполнено
	только при		µ <1 . Если		µ ≥1 , то цилиндр начнет
	скользить вместе с кубом не вращаясь, т.е. система
	будет двигаться поступательно как одно тело с мас-
рис. 2.32	сой	m3 = m1 +m2 (рис.2.32). Уравнение этого дви-
жения имеет вид:		m3a = m3 g sin α−µN3 .
Условие начала движения: m a = m g sin α−µm g cos α ≥ 0 ,						т.е. α'	=
		3		3	3	кр

=arctgµ. Этот угол больше, чем соответствующее значение угла (2.41) при µ <1 .

Гироскопический эффект

Задача 2.22

Монета катится по горизонтальной поверхности стола без скольжения с линейной скоростью vC , описывая окружность радиуса R r ( r – ради-

44	Глава 2. Динамика.

ус монеты). Найти угол наклона монеты к горизонту.

Решение

Монета вращается по кругу с угловой скоростью Ω = vC R и одновременно вращается вокруг своей оси симметрии с угловой скоростью ω = vC r . Так как по условию ω Ω = R r 1 , то монету можно считать гироскопом с моментом инерции I = mr2 2 исобственным моментом импульса

	L = Iω = mrvC				2 ,					(2.42)
где vC – скорость центра масс C монеты.
		Перейдем в неинерциальную систему отсче-
	та,		в которой центр масс C неподвижен. Все
	приложенные к гироскопу силы – тяжести
	mgG		, нормальной реакции NG , трения FGтр и
	центробежная					FGцб		– уравновешены. Как вид-
рис. 2.33	но из рис.2.33, условиями равновесия будут:
	N = mg			и	F		= F		= mΩ2 R .	(2.43)
					тр			цб
Суммарный момент этих сил относительно точки C , в соответствии с
известным уравнением движения гироскопа
		G	G		G
				= ∑MiC ,						(2.44)
	ωп, L

приводит к прецессииG гироскопа, т.е. к вращению его собственного мо-

мента импульса L вокруг оси, проходящей через "закрепленную" точку C , с угловой скоростью прецессии ωG п . Ненулевые моменты сил относи-

тельно точки C создают только силы трения и реакции, приложенные в точке O касания монеты и стола (отрезок OC = r на рис.2.33 лежит в вертикальной плоскости).

Но монета всегда наклонена к центру траектории. Поэтому угловые ско-
					G	G
рости прецессии и вращения по окружности должны совпадать: ωп = Ω .
		G	G		(π−θ). В проекции на горизонталь-
Угол между векторами Ω			и L равен		(π−θ). В проекции на горизонталь-
ную плоскость уравнение (2.44) запишется в виде:
		ΩL sin (π−θ)= N r cos θ− Fтр r sin θ .
После подстановки формул (2.42), (2.43) и связей Ω = vC R , ω= vC						r
	mv2r	sin θ = mgr cos θ−		mv2r
получим:	C			C	sin θ , откуда
получим:	2R			R	sin θ , откуда
	2R			R

точки C :

Гироскопический эффект	45
θ = arctg (2gr 3vC2 ).	(2.45)

Заметим, что если бы монета скользила по окружности радиуса R на гладкой поверхности не вращаясь, то в выбранной неинерциальной системе отсчета следовало бы записать условие равновесия моментов сил относительно

Fтр r sin θ = N r cos θ, откуда θ = arctg (gRvC2 ).

Такой угол наклона, отличный от выражения (2.45), получится, например, для конькобежца, скользящего по виражу.

Задача 2.23

Акселерометр, используемый в авиации, представляет собой гироскоп, точка подвеса которого находится выше центра масс (рис.2.34). Характеристики его таковы: масса m =100 г , момент инерции

	I = 2 10−5 кг м2 , расстояние от точки подвеса до
	центра масс l =1 см, частота вращения n =
	= 2 106 об/мин . При равномерном движении само-
	лета ось вращения гироскопа расположена верти-
	кально, при ускоренном – отклонена от вертикали.
рис. 2.34	Найти величину и направление отклонения оси ги-
рис. 2.34	роскопа в случае, когда самолет в течение t =10 c

движется с горизонтальным ускорением a =1 м/с2 .

Решение

Перейдем в неинерциальную систему отсчета, в которой точка подвеса O гироскопа неподвижна. В этой системе, помимо силы тяжести mgG , не-

нулевой момент относительно			точки O может создавать		только сила
инерции FGин = −maG	. Из уравнения движения гироскопа
		G	G	G
				= ∑M0	(2.46)
	ωп, L

следует, что гироскоп, вообще говоря, должен совершать прецессию под действием двух моментов сил. При этом ось вращения OO ' гироскопа, первоначально ориентированная вдоль вертикальной оси Oy (рис.2.34),

начнет отклоняться от вертикали на угол ϕ . Однако этот угол настолько мал, что моментом силы тяжести mgl sin ϕ можно пренебречь по сравнению с моментом силы инерции Mин ≈ mal .

Поэтому можно считать, что прецессия происходит только под действием момента MGин , и ось гироскопа во время ускорения самолета начнет

46 Глава 2. Динамика.

поворачиваться вокруг горизонтальной оси Ox (рис.2.34) с угловой скоростью прецессии ωG п . Согласно уравнению (2.46)

ωп L sin 90° = ωп I 2πn ≈ mal, откуда ωп≈ mal(2πIn).

За время ускорения угол поворота составит:

ϕ = ωпt ≈ 2maltπIn = 2,39 10−3 рад = 8, 21' .

Теперь убеждаемся в справедливости приближения: моментом сил тяжести, под действием которого ось гироскопа будет практически незаметно прецессировать вокруг вертикальной оси Oy , можно пренебречь.

Реактивное движение

Задача 2.24

Ракета массы m0 =1 т с поперечным сечением S = 5 м2 летела с выключенным двигателем и попала в облако пыли. Масса каждой пылинки

m =10−6 кг , их концентрация n =10−4						м−3 , а соударения с ракетой абсо-
1
лютно неупруги. Какова ширина облака l ,							если после пролета через него
ракета потеряла 1% скорости?
		Решение						ракета, летящая со скоро-
		За время					dt
		стью v ,				столкнется с пылью, находящейся
		в объеме Svdt (рис.2.35), и суммарная мас-
		са этой				пыли		dm = m1 n Svdt увеличит
рис. 2.35		массу ракеты. Уравнение Мещерского для
		реактивного движения запишется в виде:

m	dv	= −v	dm	=		F		(2.47)

	dt		dt			торм

(пылинки "прилипают" к ракете, создавая силу торможения).
Устраняя dt из уравнения (2.47), находим:
dv v +dm m = d (ln v +ln m)= d (ln (vm))= 0 , откуда vm = v0m0 = const
или		m = v0m0				v .		(2.48)
Подставляя найденную зависимость (2.48), а также полученное выше
приращение dm в уравнение (2.47), приводим его к виду
	dl	= vdt = −			v0m0		dv	.
					nSm1 v2

Проинтегрировав обе части с учетом того, что конечная скорость равна 0,99v0 , найдем:

Реактивное движение							47
l =	v0m0	1	−	1	=	m0	= 2,02 107 км

		0,99v0		v0
	nSm1					99 nSm1

Задача 2.25

Межпланетная станция имеет форму тора с внешним радиусом R . Для создания искуственного поля тяжести станция приводится во вращение вокруг оси симметрии с помощью двух ракетных двигателей, установленных на внешнем ободе тора на одном диаметре (рис.2.36). Через сколько времени после включения двигателей тела на станции будут иметь такой же вес, как и на Земле? Относительная скорость истечения газов u = = const , общий секундный расход топлива µ тоже постоянен, момент

инерции станции вместе с горючим равен I0 .

		Решение
	Из двигателей станции за время dt вылета-
	ют по касательной к ободу газы с суммарной
	массой dm = µdt . Поэтому на станцию дейст-
	вует суммарная	реактивная сила тяги Fр =
	= u dm dt = uµ ,	направленная также по каса-
	тельной (рис.2.36), имеющая момент Mр =
Рис. 2.36	= FрR = uµR и раскручивающаяся станцию.

Момент инерции станции с потерей топлива уменьшается за время dt работы двигателей на величину dI = dm R2 = µR2dt и в момент t будет

равен I0 −µR2t .

Уравнение вращательного движения станции (аналог уравнения Мещер-


ского при поступательном реактивном движении) принимает вид:
				(I0 −µR2t )dω dt = Mр = uµR .					(2.49)
Решим уравнение (2.49) методом разделения переменных:
dω =	µuRdt	= −	u	d (I0 −µR2t )	, откуда	ω = −	u	ln (I0 −µR2t )+const .
dω =	I0 −µR2t	= −			, откуда	ω = −		ln (I0 −µR2t )+const .
	I0 −µR2t		R I0 −µR2t				R

Из начальных условий ( ω = 0 при t = 0 ) находим постоянную интегрирования const = (u ln I0 )R , и в результате имеем:

	u			µR2
ω = −		ln 1	−			t .	(2.50)
ω = −	R	ln 1	−	I		t .	(2.50)
	R			I	0
					0

48 Глава 2. Динамика.

«Вес» тел на станции создается центробежной силой, поэтому искомое время определяется условием mg = Fцб = mω2 R . Отсюда ω = gR . Подставляя это значение в уравнение (2.54) и выражая из него время t1 , нахо-

дим:	t =	I	0				gR
			0	1	−exp	−		.
		µR2		1	−exp	−	u	.
		µR2					u

Гравитация

Задача 2.26

Однородный шар имеет массу m и радиус R . Найти обусловленное

гравитационным сжатием давление		p внутри шара как функцию расстоя-
ния r от его центра. Оценить	p в центре Земли, считая Землю однород-
ным шаром.	Решение
	Решение
Сначала, применяя теорему Гаусса,			v∫ EGгр dSG = −4πGmвнутри , найдем ве-
личину напряженности Eгр (r )	гравитационного поля в точке							r < R , где
R – радиус шара:
E 4πr2 = 4πGρ 4πr3 3			и	Е		(r )= 4πGρr 3.
гр				гр
Здесь G – гравитационная постоянная,								ρ – плот-
ность шара, m = 4πr3ρ 3 – его масса.
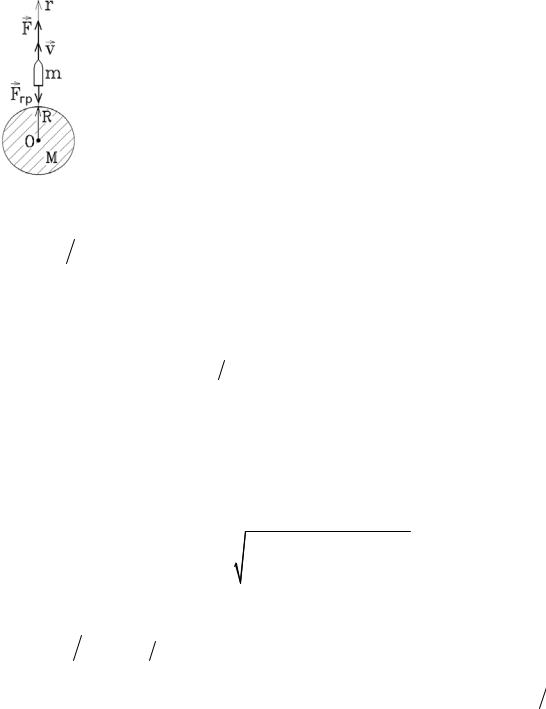
Далее выделим элемент массы dm = ρSdr									с пло-
щадью	S	на	расстоянии r от				центра		шара
(рис.2.37). Так			как	он	находится в		статическом

		равновесии, то сила гравитационного притяжения
	Рис. 2.37	G
	Рис. 2.37	dFгр к центру шара должна уравновешиваться раз-
		dFгр к центру шара должна уравновешиваться раз-
	ностью сил давления на его нижнюю и верхнюю поверхность:
		dFгр = Eгр (r ) dm = pS −(p + dp)S .

Отсюда находим приращение давления внутри шара с увеличением рас-

стояния от центра на dr :

dp = −E

dm S = −E

ρdr = −4πGρ2rdr 3.

гр

Давление уменьшается с ростом r

и равно нулю на поверхности шара.

Проинтегрировав последнее уравнение, найдем

p (r )= −

πGρ2

3Gm2

∫

dp =

∫

r dr =

−

(2.51)

8πR

где m – масса шара.

Гравитация

Формула (2.51) позволяет оценить давление в центре Земли: если учесть,

что	Gm3	= g (R	)= 9,81 м/с2 , то	p	(0)=	3	g2 (R	)=	=1,72 1011 Па ≈

	R32	3		З		8πG	3

≈1,7 106 атм .

Задача 2.27

С поверхности планеты радиуса R = 6400 км вертикально вверх взлетает ракета (рис.2.38), причем ее двигатели с момента старта развивают постоянную силу тяги F = kmg , где m –

масса ракеты, g =10 м/с2 – ускорение свободного падения на

поверхности планеты, k = 2 . Какое время τ должны работать двигатели ракеты, чтобы она приобрела вторую космическую скорость vII и навсегда покинула планету? Вращением плане-

ты и присутствием атмосферы пренебречь.

рис. 2.38 Решение

Так как ускорение свободного падения на поверхности планеты

g = GM R2 , где M – масса планеты,

G – гравитационная постоянная, то

уравнение движения ракеты имеет вид

GMm

= F − F

= kmg −

= mg k −

(2.52)

гр

Подставляя связь dt = dr v , разделяем переменные и интегрируем обе

части уравнения (2.52):

∫

vdv = g

k −

dr,

откуда

2 = 2g kr +

+const .

(2.53)

∫

Постоянную интегрирования находим из начальных условий: v = 0

при

r = R . Поэтому const = −2gR (k +1) и

v =

2gR k

−k −1

(2.54)

Второй космической скорости ракета достигнет на таком удалении r ' от центра планеты, когда ее механическая энергия станет равной нулю:

E = mvII2	2 −GMm r ' = 0 . Из последней формулы и из формулы (2.53) на-
ходим vII2		2gR2		R2	−2gR (k +1), откуда	r ' = R (k +1) k .
	=		= 2g kr '+
	=	r '	= 2g kr '+	r '
		r '		r '

50 Глава 2. Динамика.

Чтобы получить время ускорения τ, разделяем переменные в уравнении (2.54) и вычисляем интеграл:

r '		r		R			1	r '	rdr
τ = ∫ dr								∫
	2gR k		+		−k −1	=				.	(2.55)
		R		r					kRr2 −(k +1)Rr + R2
R							2g R

Интеграл в правой части формулы (2.55) не вычисляется в элементарных функциях. Численное интегрирование с помощью ЭВМ после подстановки числовых значений позволяет выразить результат с помощью следующей таблицы:

k	1,5	2	3	4	5	10	20
τ, мин	19,2	12,6	7,53	5,38	4,19	1,98	0,97

Заметим, что при k = 2 космонавт испытывает двойную силу тяжести в момент старта.

<<< < Предыдущая 1 2 3 45 / 195 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Соседние файлы в папке Колмаков Ю.Н. Лекции по физике ТулГУ. Механика

#
02.05.20143.9 Mб86mech-lec-TulGU.pdf
#
02.05.20143.32 Mб540mech-zad-TulGU.pdf