
Колмаков Ю.Н. Лекции по физике ТулГУ. Механика / mech-zad-TulGU
.pdf
Криволинейное ускоренное движение. |
11 |
Rкр = v 2 an будет наименьшим в верхней точке траектории, |
где нор- |
мальное ускорение максимально и равно ускорению свободного падения (an = g ), а скорость становится наименьшей (v = v0 cos α). Поэтому
(Rкр ) |
|
|
v |
2 cos2 |
α |
|
|
|
= |
|
0 |
|
≥ R. |
(1.8) |
|
min |
|
g |
|
||||
|
|
|
|
|
|
Из условия исчезновениявертикальнойпроекции скорости v0 sin α− gt = 0 определяем время подъема камня на наибольшую высоту: t = v0 sin α g . Эта высота совпадает с высотой сферы(рис.1.8).
g . Эта высота совпадает с высотой сферы(рис.1.8).
|
gt2 |
|
v |
2 sin2 |
α |
|
|
h = v sin α t − |
|
= |
|
0 |
|
= 2R . |
(1.9) |
|
|
|
|
||||
0 |
2 |
|
|
2g |
|
|
|
|
|
|
|
|
|
Используя теперь тривиальное равенство sin2 α+cos2 α =1 , получаем из
соотношений (1.8) и (1.9), что |
4gR |
+ |
gR |
≤1 , т.е. v |
0 min |
= |
5gR и |
||
|
v2 |
||||||||
|
|
v |
2 |
|
|
|
|
||
α = arcsin ( |
0,8 )= 63o26' . |
0 |
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|||
Задача 1.9.
Найти величину ускорения тела, соскальзывающего без начальной скорости по винтовому желобу с шагом h и радиусом R (рис.1.9) в конце n -го витка. Найти также время соскальзывания. Трение считать пренебрежимо малым.
Решение
Движение по винтовой (спиральной) линии можно представить в виде
суммы двух движений: вращения по окружности радиуса |
R в горизон- |
|||
тальной плоскости и одновременного падения вертикально вниз. |
||||
|
|
Свободное |
скольжение |
|
|
|
тела происходит под дейст- |
||
|
|
вием проекции силы тяже- |
||
|
|
сти на направление траек- |
||
|
|
тории. Так как траектория |
||
|
|
наклонена к горизонту под |
||
|
|
углом α (рис.1.9), то вдоль |
||
рис.1.9 |
рис.1.10 |
траектории тело будет дви- |
||
гаться с касательным уско- |
||||
|
|
|||
рением g sin α , где |
g – ускорение свободного падения (рис.1.10). Разло- |
|||
жив это ускорение на вертикальную и горизонтальную проекции, нахо-

12 Глава 1. Кинематика
дим, что тело движется вниз с ускорением aв = (g sin α) sin α и одновре-
менно вращается |
по |
окружности |
с тангенциальным ускорением |
|||
a |
= (g sin α) cos α |
и |
нормальным |
ускорением |
a |
= (v ')2 R , где |
τ |
|
|
|
|
n |
|
v ' = v cos α – проекция скорости тела на горизонтальное направление. Зная проекции ускорения на три взаимно перпендикулярных направления (рис.1.9), легко найти полное ускорение тела:
a = a2 |
+a2 |
+a2 |
= |
g2 sin2 α+(v cos α)4 R2 . |
(1.10) |
в |
n |
τ |
|
|
|
На рис.1.10 один виток траектории "развернут" на вертикальной плоскости, и видно, что sin α = h l, cos α = 2πR
l, cos α = 2πR l , где l = h2 +4π2 R2 – длина
l , где l = h2 +4π2 R2 – длина
одного витка.
Так как трение отсутствует, а силы нормальной реакции работу над телом не производят, то из закона сохранения энергии mgH = mv2  2 следует, что спустившись с высоты n витков H = hn , тело приобретет скорость v = 2ghn . После подстановки в формулу (1.10), находим искомую величину ускорения в конце пути:
2 следует, что спустившись с высоты n витков H = hn , тело приобретет скорость v = 2ghn . После подстановки в формулу (1.10), находим искомую величину ускорения в конце пути:
a = |
g2h2 |
4g2h2n2 (2πR)4 |
|
gh |
h2 + 4π2R2 (1+16π2n2 ). |
|
|
+ |
|
= |
|
||
h2 + 4π2R2 |
R2 (h2 + 4π2R2 )2 |
h2 + 4π2R2 |
||||
Время соскальзывания легко определить для вертикальной проекции движения:
|
a t2 |
|
2hn |
|
2hn |
|
|
2n(h2 + 4π2R2 ) |
|
|
H = h n = |
в |
, откуда t = |
|
= |
|
|
|
= |
|
. |
2 |
a |
g sin |
2 |
|
gh |
|||||
|
|
|
α |
|
||||||
|
|
|
в |
|
|
|
|
|
|
|
Задача 1.10
По наклонному желобу, имеющему форму вогнутой циклоиды (рис.1.11), соскальзывает без трения небольшая шайба. Найти время соскальзывания шайбы с высоты h до нижней точки желоба.
Решение
Циклоида – это кривая, которую описыварис. 1.11 ет точка, находящаяся на ободе колеса, которое катится равномерно и без проскальзывания. В параметрической
форме уравнение циклоиды имеет вид:
x = R (ϕ−sin ϕ); y = R (1−cos ϕ),

Криволинейное ускоренное движение. |
13 |
где R – радиус колеса, ϕ – угол поворота, а точкам x = 0, πR, 2πR соответствуют углы поворота 0, π, 2π .
Пусть в начальный момент времени шайба находилась в точке (x0 , y0 ) и имела нулевую начальную скорость v0 = 0 . В произвольный момент време-
ни t > 0 |
она окажется в точке (x, y), |
и ее скорость возрастет до величины |
||||||||||
v = |
2g (y − y0 ) |
(так как трение отсутствует, эту формулу легко получить |
||||||||||
из закона сохранения энергии: |
mv2 |
= mg (y − y )). |
|
|||||||||
|
|
|
||||||||||
|
|
|
|
|
2 |
|
|
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
Для дальнейшего решения перейдем к угловой координате ϕ . Тогда |
||||||||||||
|
|
|
v = |
2g (y − y0 ) = |
2gR (cos ϕ0 −cos ϕ) . |
|
||||||
Но |
v = dl dt , |
а |
элемент |
длины |
траектории dl = |
(dx)2 +(dy)2 = |
||||||
= (R − R cos ϕ)2 +(R sin ϕ)2 dϕ = R |
2 |
(1−cos ϕ)dϕ = 2R sin |
ϕdϕ . Следова- |
|||||||||
|
|
v = 2gR (cos ϕ0 −cos ϕ) = 2R sin ϕ |
dϕ |
|
2 |
|||||||
тельно |
. Разделяя |
в последнем |
||||||||||
|
||||||||||||
|
|
|
|
|
|
|
|
2 dt |
|
|||
уравнении переменные и интегрируя, находим время соскальзывания |
|||||||||||||||||||
шайбы из точки с координатами x0 , y0 в точку с координатами x, y : |
|||||||||||||||||||
|
|
|
ϕ |
|
ϕ |
|
|
|
|
R |
ξ |
|
|
dξ |
|
|
|||
|
|
|
2R sin 2 dϕ |
|
|
|
|
|
|
|
|
||||||||
|
t = ∫ |
|
|
|
|
|
|
= −2 |
|
|
∫ |
|
|
|
. |
||||
|
|
2gR (cos ϕ0 −cos ϕ) |
|
|
g |
|
|
ξ2 −ξ2 |
|||||||||||
|
|
|
ϕ |
|
|
|
ξ |
0 |
|
|
|
||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||||
Здесь использована замена переменной: |
cos ( |
ϕ 2)= ξ . |
|
Отсюда следует, |
|||||||||||||||
что |
dξ = − |
1 |
sin |
ϕdϕ |
или |
sin |
ϕd |
ϕ = −2dξ, |
|
|
а |
также |
cos ϕ0 −cos ϕ = |
||||||
|
|
||||||||||||||||||
|
2 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
(ξ02 −ξ2 ). |
|||
= (1+cos ϕ0 )−(1+cos ϕ)= 2 |
|
ϕ |
−cos2 |
ϕ |
|
|
|
||||||||||||
cos2 |
0 |
|
= 2 |
||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
||
Нижней точке желоба соответствует угол ϕ = π, поэтому в верхнем пре-
деле ξ = cos |
ϕ |
= cos |
π = 0 , а искомое время: |
|
|
|
|
|
|||||||||
|
2 |
|
|
|
2 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
R |
0 |
|
dξ |
|
R |
|
ξ |
|
|
|
R |
arcsin (1)= π |
R |
|
||
|
|
|
|
|
|
|
|||||||||||
t = −2 |
∫ |
|
= −2 |
arcsin |
|
|
|
= 2 |
. |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
g |
ξ |
0 |
ξ2 −ξ2 |
|
g |
ξ0 |
|
ξ |
0 |
g |
g |
|||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
Итак: время соскальзывания шайбы не зависит от высоты или от на-

14 |
Глава 1. Кинематика |
чальной точки соскальзывания! Кривые или поверхности с таким свойством называются изохронными.
В 1673 г. Х. Гюйгенс доказал, что циклоида – единственная изохронная кривая. А в 1696 г. И.Бернулли показал, что циклоида, к тому же, является брахистохроной, т.е. кривой, время соскальзывания по которой с данной высоты является наименьшим. Вспомните, какую форму имеют крыши индийских пагод!
Кинематика вращательного движения.
Задача 1.11
Якорь электромотора, вращавшийся с частотой ν0 =50 Гц, после выклю-
чения тока, двигался с угловым ускорением, линейно убывающим с течением времени, и остановился через τ =10 с, сделав до остановки N = 300 оборотов. Найти зависимость углового ускорения от времени в явном виде.
Решение
Согласно условию задачи, ε = α−βt .Поэтому
ω = ∫εdt = ωo +αt −βt2  2 ,
2 ,
где ω0= 2πν0 – начальная угловая скорость вращения. Так как ω = 0 при
t = τ , то |
|
|
|
ω0 = −ατ+βτ2 2 . |
|
|
|
(1.11) |
||
Далее, поскольку ϕ = ∫ω dt = ω0t +αt2 |
2 −βt3 |
6 , то |
|
|
||||||
N = ϕ(τ) 2π = ν0τ+ατ2 4π−βτ3 12π . |
(1.12) |
|||||||||
Из уравнений (1.11) и (1.12) находим: |
|
|
|
|
|
|
||||
|
4π |
3N |
|
|
12π |
(2N |
|
τ). |
||
α = |
|
|
|
−2ν0 ; |
β = |
|
|
−ν0 |
||
τ |
τ |
τ3 |
|
|||||||
|
|
|
|
|
|
|
|
|||
Подстановка численных значений в эти выражения дает: α = −4π с−2 и
β =1, 2π c−3 . Таким образом, ε = −4π(1+0,3t ) c−2 .
Задача 1.12
Твердое тело вращается вокруг неподвижной оси так, что его угловое ускорение меняется по закону ε = ε0 (1−αϕ), где ε0 и α – положительные константы, а ϕ – угол поворота. Найти зависимость угловой скорости от угла поворота и описать характер движения. Известно, что ω = 0 при ϕ = 0 .
Решение
Из определения угловой скорости следует, что dω= εdt = ε0 (1−αϕ)dt.

Кинематика вращательного движения. |
15 |
Но dt = dϕ dω, поэтому ωdω= ε0 (1−αϕ)dϕ . Интегрируя это дифференциальное уравнение с учетом начального условия, находим:
dω, поэтому ωdω= ε0 (1−αϕ)dϕ . Интегрируя это дифференциальное уравнение с учетом начального условия, находим:
ω |
ϕ |
ϕ |
т.е. |
ω2 |
|
ϕ2 |
||
|
|
|||||||
∫ωdω= ε0 ∫dϕ−αε0 ∫ϕ dϕ, |
|
2 |
= ε0 |
ϕ−α |
, |
|||
0 |
0 |
0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
откуда |
|
ω= ± ε0ϕ(2 −αϕ) . |
|
|
|
(1.13) |
||
|
|
Применив к полученному результату условие |
||||||
|
|
экстремума |
dω2 dϕ |
ϕ=ϕm |
= 2ε0 (1 −αϕm )= 0, оп- |
|||
|
|
|
|
|
|
|
|
|
|
|
ределяем, что величина угловой скорости дос- |
||||||
|
|
тигает максимума при ϕm =1 α и обращается в |
||||||
рис. 1.12 |
|
нуль при ϕ = 0 и ϕ = 2 α . Зависимость ω(ϕ) |
||||||
показана на рис.1.12 (при положительных ε0 |
|
и α угол ϕ не может при- |
||||||
нимать отрицательных значений).
Движение, о котором идет речь – колебания около положения равновесия ϕ =1 α с амплитудой ϕm =1
α с амплитудой ϕm =1 α . Из формулы (1.13), в силу того, что
α . Из формулы (1.13), в силу того, что
ω = dϕ dt , следует: |
|
± |
|
|
|
dϕ |
|
= dt |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
ε0ϕ(2 −αϕ) |
|
|
|
|
|
|
||||||||||
Интегрируя это уравнение, находим зависимость угла поворота от вре- |
||||||||||||||||||||||
мени. В частности период колебаний будет |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
ϕ=2 |
α |
|
|
dϕ |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
T = 2 ∫ |
|
|
|
|
|
|
. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
ϕ=0 2ε0ϕ−ε0αϕ2 |
|
|
|
|
|
|
||||||||
С помощью замены переменной ϕ = ξ2 |
приходим к известному интегралу |
|||||||||||||||||||||
|
4 |
2 |
α |
dξ |
|
|
|
|
4 |
|
|
|
α |
|
|
ξ= |
2 α |
2π |
. |
(1.14) |
||
|
|
|
|
|
|
|
|
|||||||||||||||
T = |
∫ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
= |
|
|
|
arcsin |
2 |
ξ |
|
|
= |
|
||||||
ε0α 0 |
|
|
|
|
|
ε0α |
|
|
ε0α |
|||||||||||||
|
|
|
2 α −ξ2 |
|
|
|
|
ξ=0 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
К этому результату можно прийти намного быстрее, если привлечь на помощь динамику, где доказывается, что уравнение гармонических колебаний в канонической форме имеет вид:
x |
+ω2 x = 0 |
или |
ϕ+ω2ϕ = 0 |
, |
|
0 |
|
0 |
|
где ω0 – циклическая частота колебаний. Тогда условие задачи можно записать в виде
|
d 2ϕ |
|
|
|
d 2ϕ |
|
|
|
ε = |
|
= ε0 |
−ε0αϕ |
или |
1 |
+ε0αϕ1 = 0 , |
(1.15) |
|
dt2 |
dt2 |
|||||||
|
|
|
|
|
|

16 Глава 1. Кинематика
где ϕ1 = (ϕ−1 α) – новая угловая переменная (угол поворота, отсчитываемый от положения равновесия ϕ1 = 0 ). Из уравнения (1.15) сразу сле-
α) – новая угловая переменная (угол поворота, отсчитываемый от положения равновесия ϕ1 = 0 ). Из уравнения (1.15) сразу сле-
дует, что ω0 = ε0α или T = 2π ω0 = 2π
ω0 = 2π ε0α
ε0α
– в полном согласии с формулой (1.14).
Сложение скоростей.
Задача 1.13
На одном конце бесконечно растяжимого шнура длины l =1 м сидит жук,
тогда как другой конец шнура закреплен в стене. В начальный момент времени t = 0 шнур начали растягивать, перемещая свободный конец шнура с
постоянной скоростью v0 =1 м/с, а жук пополз по шнуру к стене с постоянной скоростью u = 0,1 м/с . За какое время τ жук доползет до стены?
Решение
Направим ось x вдоль скорости растягиваемого шнура (рис.1.13,а). Правый конец шнура удаляется от стены со скоростью v0 , и в момент t находится на расстоянии l +v0t , а левый конец шнура неподвижен. По-
этому скорость любой точки шнура пропорциональна ее удалению x от
стены, как показано на рис.1.13,б: v (x)= l +xv0t v0 .
Пусть x |
– координата жука, который |
|
|
|||
двигается вместе со шнуром со скоро- |
|
|
||||
стью v (x) |
и дополнительно ползет со |
|
рис. 1.13 |
|||
скоростью u относительно шнура. Его скорость относительно стены: |
||||||
|
|
dx |
|
x v0 |
|
(1.16) |
|
|
dt |
= v (x)−u = l +v t |
−u. |
||
|
|
|
||||
|
|
|
0 |
|
|
|
Остается решить это дифференциальное уравнение с учетом начальных
условий: x0 = l |
при t = 0 . Сделаем замену переменной x = (l +v t)ξ . То- |
||||||||||||||||
|
dx |
|
|
dξ |
|
|
v0 x |
|
|
|
|
|
|
|
|
|
0 |
гда |
= (l +v t) |
+ |
|
|
, и подстановка в уравнение (1.16) позволяет |
||||||||||||
|
dt |
0 |
|
dt |
l +v0t |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
dξ |
|
|
|
|
|
|
|||||||
привести его к виду |
|
|
|
(l +v0t ) |
= −u. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
||
Разделяя переменные и интегрируя, получаем |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
u dt |
|
|
u |
|
|
v |
|
|
||
|
|
|
dξ = − |
|
|
|
и ξ = − |
|
|
ln 1 |
+ |
0 |
t |
+ξ0 . |
|||
|
|
|
|
l +v0t |
v0 |
l |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Сложение скоростей. |
17 |
Начальные условия x0 = l ξ0 = l |
дают постоянную интегрирования ξ0 =1. |
Возвращаясь к переменной x, получаем искомое решение уравнения (1.16):
x = (l +v t ) 1− |
u |
ln |
1+ |
v0t |
. |
(1.17) |
|
|
|
||||||
0 |
|
v0 |
|
|
l |
|
|
|
|
|
|
|
|
||
Полагая в формуле (1.17) x = 0 в тот момент времени t = τ , когда жук доползет до стены, находим:
τ = l |
(exp (v0 u)−1)= exp (10)−1 = 6,12 час. |
v |
|
0 |
Задача 1.14 |
|
В тот момент времени, когда центр катящегося без скольжения со скоростью v0 колеса радиуса R находился в точке C (рис.1.14), с его обода
сорвался застрявший камешек и пролетел через точку C . На какую максимальную высоту h над поверхностью земли взлетит этот камешек?
Решение
Катящееся колесо совершает два движения – поступательное со скоростью v0 вдоль оси x и
вращательное с угловой скоростью ω = v0  R .
R .
Скорости этих движений складываются векторно, и камешек, оторвавшийся в точке A (рис.1.14), имеет проекции скорости vx0 = v0 −v0 cos α ,
vy0 = v0 sin α . Он летит за колесом вдоль оси x
(если на автомобили не ставить брызговиков, то за ними будет лететь шлейф грязи, догоняющий автомобиль при его резком торможении). Условие пролета камешка в некоторый момент времени t1 через точку
C , в которой в начальный момент |
t0 = 0 |
находился центр колеса, |
дает |
||||||||
кинематические соотношения: |
|
|
|
|
|
|
|
|
|
|
|
OC = R = R (1−cos α)+v |
|
|
gt2 |
|
|
|
|
|
|||
t − |
|
1 |
|
|
и |
AB = R sin α = v t . |
|
||||
|
|
|
|
|
|||||||
0 y 1 |
|
|
2 |
|
|
|
0 x 1 |
|
|||
|
|
|
|
|
|
|
v0 (1−cos α)=(R ctg |
|
) |
|
|
Исключая из этих формулвремя t1 = Rsin α |
α |
v0 , |
|||||||||
2 |
|||||||||||
получаем уравнение для определения неизвестного угла α : |
|
||||||||||
ctg2 |
α |
|
|
2v2 |
|
|
|
|
|
||
2 |
= |
0 |
. |
|
(1.18) |
||||||
|
|
||||||||||
|
|
|
gR |
|
|
|
|
|
|||
Время подъема камешка до наивысшей точки t2 = v0 y g = v0 sin α g , а

18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Глава 1. Кинематика |
||
высота подъема над уровнем земли |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
gt2 |
|
|
|
|
|
v2 |
||||
h = R (1−cos α)+v t |
2 |
− |
|
2 |
= R (1 |
−cos α)+ |
0 |
sin2 α . |
||||||||||||
|
|
|
||||||||||||||||||
|
|
|
|
0 y |
|
2 |
|
|
|
|
|
|
|
2g |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
); |
||||
Учитывая, что 1−cos α = 2sin2 |
α |
= 2 |
(1+ctg2 |
α |
|
|
||||||||||||||
2 |
2 |
|
|
|||||||||||||||||
sin2 α = 4sin2 |
α |
cos2 |
α |
= ctg2 |
α |
|
(1+ctg2 |
α |
)2 |
, и подставляя соотношение |
||||||||||
2 |
2 |
2 |
2 |
|||||||||||||||||
(1.18) , находим: |
|
(gR +v02 ) |
2 |
+v04 |
|
|
||||||||||||||
|
|
|
|
h = 2R |
|
|
|
|||||||||||||
|
|
|
|
|
(gR + 2v02 )2 . |
|
|
|||||||||||||
Задача 1.15
Два твердых тела вращаются вокруг неподвижных взаимно перпендикулярных осей с постоянными угловыми скоростями ω1 = 3 рад/с и ω2 =
= 4 рад/с. Найти угловую скорость и угловое ускорение одного тела относительно другого.
Решение
Рассмотрим систему O ' , в которой первое тело неподвижно, и которая вращается вместе с первым телом вокруг оси z ' с угловой скоростью ωG1 . В этой системе ось вращения z '' вто-
рого тела дополнительно будет вращаться в противоположную сторону с угловой скоро-
стью (−ωG1 ), как показано на рис.1.15. Угловые
скорости вращения второго тела складываются, рис. 1.15 и получается угловая скорость вращения второ-
го тела относительно неподвижного первого:
ωGотн = ωG2 +(−ωG 1 )= ωG2 −ωG 1 ,
в соответствии с определением относительной скоро-
сти. Ее величина ωотн = |
ω12 +ω22 = 5 рад/с постоянна, |
|
рис. 1.16 |
|
но направление изменяется. Поэтому относительное |
|
|||
|
|
|||
ускорение неGравно нулю. |
G |
G |
|
G |
Вектор (−ω1 ) не изменяется. Поэтому εотн = dωотн |
dt = dω2 dt . Как |
|||
видно из треугольника на рис.1.16, приращение вектора |
G |
за время dt |
||
ω2 |
||||
будет равно (по модулю) |
dω2 = радиус×угол поворота = ω2 ω1dt . С уче- |
|||

Переход в неинерциальную систему отсчета. |
|
|
|
19 |
||||
том направления получим |
|
|
|
|
|
|
||
G |
G |
G |
и |
εотн = ω2 |
ω1 |
=12 рад/с |
2 |
. |
εотн =[ω2 |
, ω1 ] |
|
||||||
Задача 1.16
Нить, намотанную на ось катушки, тянут со скоростью v под углом α к горизонту. Вследствие этого катушка катится по горизонтальной плоскости без скольжения. Найти скорость центра масс и угловую скорость вращения катушки. При каком условии катушка движется а) в сторону движения нити? б) в противоположную сторону? Радиусы центральной части катушки и ее обода равны соответственно r и R .
Решение
В неподвижной системе K , связанной с горизонтальной плоскостью, катушка совершает два движения: поступательное со скоростью vGC и вращательное с
рис. 1.17 угловой скоростью ωG (рис.1.17,а). Так как скольжения нет, то точка касания B неподвижна и
ωR = vC . |
|
|
A нити в этой системе. Перейдем в систему |
|||||||
Пусть v |
– скорость точки |
|||||||||
K ' , связанную с центром масс C катушки (рис.1.17,б). В новой системе |
||||||||||
катушка только вращается вокруг оси C , а нить наматывается на нее со |
||||||||||
скоростью |
ωr . |
По теореме сложения скоростей точка |
A в системе K ' |
|||||||
имеет скорость |
vG' = vG−vG , |
проекция которой на ось |
x ' , направленную |
|||||||
|
|
C |
|
|
|
|
|
|
|
|
вдоль нити, равна по величине скорости намотки (рис.1.17,б): |
|
|||||||||
|
|
v 'x = v −vC cos α = −ωr = −vC r R |
|
|
|
|||||
(знак "–" показывает, что проекция скорости намотки на ось x ' |
отрица- |
|||||||||
тельна). Отсюда |
vC = |
v |
; |
ωz = |
v |
|
. |
(1.19) |
||
|
|
|
||||||||
cos α−r R |
R cos α−r |
|||||||||
|
|
|
|
|
|
|
||||
Из соотношений (1.19) сразу следует, что |
|
|
|
|
|
|||||
vC > 0 |
при |
cos α > r R (нить наматывается на катушку), |
(1.20) |
|||||||
vC < 0 |
при |
|
|
|
|
|
|
|
||
cos α < r R (нить разматывается с катушки). |
|
|||||||||
Переход в неинерциальную систему отсчета.
Задача 1.17
На клин, плоскость которого составляет угол ϕ с горизонтом, положили
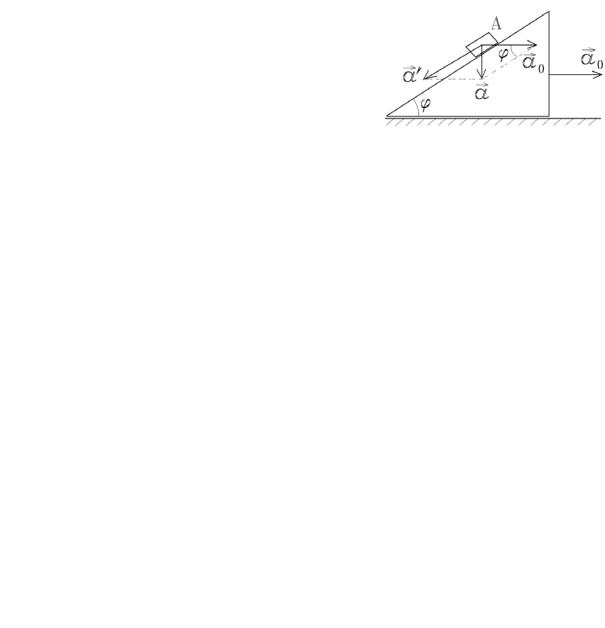
20 |
Глава 1. Кинематика |
шайбу А (рис.1.18). Какое ускорение a0 |
не- |
обходимо сообщить клину в горизонтальном направлении, чтобы шайба А свободно падала вертикально вниз? Трением шайбы о клин пренебречь.
Решение
Согласно формуле преобразования ускорис. 1.18 рений aG = aG0 +aG' , где aG и aG' – ускорения
шайбы относительно Земли и клина соответственно. Но по условию задачи aG = gG . Поэтому, используя рис.1.18, находим a0 = gctgϕ.
Задача 1.18
Снаряд выстреливается с поверхности Земли на экваторе вертикально вверх с начальной скоростью v0 =1 км/с. На каком расстоянии l от точки
выстрела и в каком направлении он упадет на Землю?
Решение
Система отсчета, связанная с Землей, вращается с постоянной угловой скоро-
стью ω = 7, 27 10−5 |
рад/с. В этом слу- |
чае ускорение тела |
aG в инерциальной |
системе отсчета связано с ускорением |
||||||||||
тела aG' |
во вращающейся системе соот- |
|||||||||
ношением ([1], стр. 24) |
|
|||||||||
G |
G |
|
|
[ |
G G |
] |
2 G |
|
||
a = g + |
2 |
ω , v |
−ω R , |
или |
||||||
|
' |
|||||||||
G |
G |
[ |
G |
G |
] |
|
2 G |
|
||
a ' = g −2 |
|
|
|
+ω R , |
(1.21) |
|||||
|
ω , v ' |
|||||||||
где второе слагаемое в правой части – кориолисово ускорение, а третье слагаемое – центростремительное ускорение, которое, изменив знак, стало цен-
тробежным, и направлено от оси вращения.
Направим ось координат x ' вдоль экватора, ось y ' – вертикально, а ось
z ' – вдоль оси вращения Земли, как показано на рис.1.19. Тогда второе слагаемое в правой части (1.21) можно представить, как
G G |
']= 2 |
|
iG |
Gj |
kG |
|
G |
G |
2ωv 'x , |
|
|
||||||||
−2[ω,v |
|
0 |
0 |
−ω |
|
= i |
2ωv' y − j |
||
|
|
|
v'x |
v'y |
v'z |
|
|
|
|
|
|
|
|
|
=a 'x |
|
откуда заключаем, что кориолисово ускорение вызывает отклонение сна-
