
Предел функции в точке.
Пример.
Используя
определение, доказать, что функция

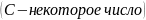 в
точке
в
точке
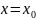
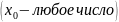 имеет предел, равный
имеет предел, равный
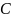 ,
т.е.
,
т.е.
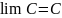
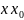
Решение.
В данном примере
,
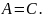 Возьмем любое
Возьмем любое
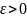 .
Тогда для любого числа
.
Тогда для любого числа
 .
.
Теоремы о пределах.
Непрерывность функции.
Производная. Геометрический и физический смысл.
Вычисление производных.
Если в функции u = u(x) и v = v(x) имеют производные в точке x0, то сумма, разность, произведение и частное этих функций (частное при условии, что v(x) ≠ 0) также имеют производные в точке x0 и справедливы следующие формулы:
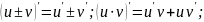
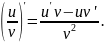
Производная сложной функции
Если функция x=(t) имеет производную в точке f0, а функция y=f(x) имеет производную в точке x0 = (t0),то сложная функция f[(t)] имеет производную в точке t0 и имеет место следующая формула:
y(t0) = f(x0) (t0).
Формула дифференцирования вместе с правилами дифференцирования суммы, разности, произведения, частного и правилом дифференцирования сложной функции составляют основу дифференциального исчисления.
Вычисление производной сложн6ой функции.
В предыдущей теореме рассматривалась сложная функция, где y зависела от t через промежуточную переменную x. Возможна и более сложная зависимость – с двумя, тремя и большими числом промежуточных переменных, но правило дифференцирования остается прежним.
Так, например, если y = f(x), где x = (u), а u = (v) и v = (t), то производную y(t) следует искать по формуле
y(t) = y(x) x(u) u(v) v(t)
Рассмотрим примеры дифференцирования сложной функции:
1.Вычислить производную y = earctgx.
Решение. Данную функцию можно представить в виде y = eu, где u = arctgx. Тогда, по формуле y(t) = y(x) x(u) u(v) v(t)
y(x)
= y(u)
u(x)
= eu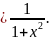
Заменив u на arctgx, окончательно получим
y(x) = earctgx
2.Вычислить производную функции y = tg2 (x2 + 1)
Решение. Данную функцию можно представить в виде y = u2, где u= tgv, а u = x2 + 1. Используя формулу y(t) = y(x) x(u) u(v) v(t). Получим
y(x) = y(u) u(v) v(x) = (u2) (tgv) (x2 + 1) = 2u sec2v 2x = 2tg (x2 + 1) sec2 (x2 + 1) 2x = 4x tg (x2 + 1) sec2 (x2 + 1).
Вычисление производной в последнем примере можно записать в таком виде:
y(x)
= 2tg (x2
+ 1)
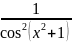 (x2
+ 1) = 2tg (x2
+ 1)
sec2
(x2
+ 1) 2x
= 4x tg (x2
+ 1) sec2
(x2
+ 1).
(x2
+ 1) = 2tg (x2
+ 1)
sec2
(x2
+ 1) 2x
= 4x tg (x2
+ 1) sec2
(x2
+ 1).
Производная обратных тригонометрических функций.
Производные высших порядков.
Производная
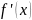 функции
функции
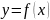 сама
является некоторой функцией аргумента
x.
Следовательно, по отношению к ней снова
можно ставить вопрос
о существовании
и нахождении производной.
сама
является некоторой функцией аргумента
x.
Следовательно, по отношению к ней снова
можно ставить вопрос
о существовании
и нахождении производной.
Назовём производной первого порядка.
Производная от производной некоторой функции называется производной второго порядка (или второй производной). Производная от второй производной называется производной третьего порядка (или третьей производной) и т.д. Производные, начиная со второй, называются производными высшего порядка и обозначаются так:
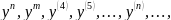
или
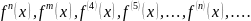
Производная
n-го
порядка есть производная от производной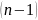 –го
порядка, т.е.
–го
порядка, т.е.
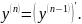
Производные
высших порядков имеют широкое применение
в физике. Здесь мы ограничимся физическим
толкованием второй производной
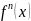 .
Если функция
описывает
закон движения материальной точки по
прямой линии, то как известно, первая
производная
есть
мгновенная скорость точки в момент
времени x,
а вторая производная в таком случае
равна скорости изменения скорости, т.е.
ускоренью движущейся точки в момент
времени x.
.
Если функция
описывает
закон движения материальной точки по
прямой линии, то как известно, первая
производная
есть
мгновенная скорость точки в момент
времени x,
а вторая производная в таком случае
равна скорости изменения скорости, т.е.
ускоренью движущейся точки в момент
времени x.
Пример.
Найти производные второго порядка от
следующих функций:
1)
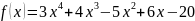 ;
2)
;
2)
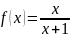 ;
3)
;
3)
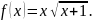
Решение. 1) Прежде всего находим первую производную:
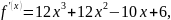
затем, считая первую производную функцией от x, берём производную от этой функции, получаем
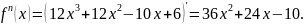
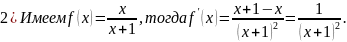
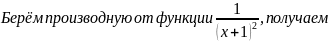
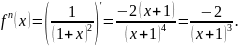
3)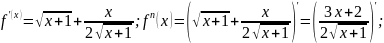
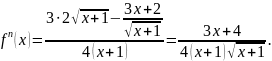
Возрастание и убывание функций. Будем говорить, что функция f(x) не убывает (не возрастает) на множестве X, если для любых x1 и x2, принадлежащих X, удовлетворяющих условию x1
 x2
, справедливо
неравенство
x2
, справедливо
неравенство
Неубывающие и невозрастающие функции объединяют общим названием монотонные функции.
Если
для любых x1
и x2,
принадлежащих X,
удовлетворяющих условию
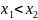 ,
справедливо неравенство
,
справедливо неравенство
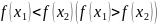 ,
то, как мы уже знаем, функция f(x)
называется
возрастающей (убывающей) на множестве
X.
Возрастающие и убывающие функции
называются также строго монотонными.
,
то, как мы уже знаем, функция f(x)
называется
возрастающей (убывающей) на множестве
X.
Возрастающие и убывающие функции
называются также строго монотонными.
Следующая теорема устанавливает важный для решения практических задач признак возрастания и убывания функции и указывает правило для определения промежутков, на которых функция возрастает и убывает.
Теорема.
Если функция f(x)
имеет производную в каждой точке на
интервале (a,
b)
и
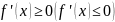 на (a,
b),
то функция f(x)
не убывает (не возрастает) на (a,
b).
на (a,
b),
то функция f(x)
не убывает (не возрастает) на (a,
b).
Замечание.
Теорема остается справедливой, если
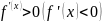 на (a,
b),
то f(x)
возрастает (убывает) на (a,
b).
на (a,
b),
то f(x)
возрастает (убывает) на (a,
b).
Правило.
Для определения промежутков возрастания
и убывания следует решить неравенства
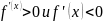 .
.
При решении задач, в которых требуется определить промежутки возрастания и убывания функции, следует прежде всего определить область существования этой функции.
Пример:
Определить промежутки, на которых
функция
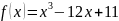 возрастает и убывает.
возрастает и убывает.
Решение.
Область определения функции – вся
числовая прямая. Находим производную
функции
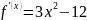 .
Из неравенства
.
Из неравенства
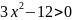 или
или
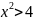 ,
или
,
или
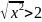 ,
т.е.
,
т.е.
 (либо
(либо
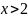 ,
либо
,
либо
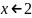 ),
следует, что данная функция возрастает
на интервалах
),
следует, что данная функция возрастает
на интервалах
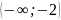 и
и
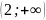 ,
а из неравенства
,
а из неравенства
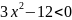 или
или
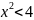 ,
или
,
или
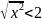 ,
т.е.
,
т.е.
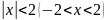 ,
следует, что данная функция убывает на
интервале (- 2; 2).
,
следует, что данная функция убывает на
интервале (- 2; 2).
Отыскание точек локального экстремума функции.
Определение.
Точка x0
называется точкой строгого локального
максимума (минимума) функции f
(x),
если для всех x
из некоторой
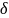 – окрестности точки x0
выполняется
неравенство f
(x)
< f
(x0)
(f
(x)
> f
(x0)).
– окрестности точки x0
выполняется
неравенство f
(x)
< f
(x0)
(f
(x)
> f
(x0)).
Из определения следует, что понятие экстремума носит локальный характер в том смысле, что в случае экстремума неравенство f (x) < f (x0) (f (x) > f (x0)) не обязано выполняться для всех значений x в области определения функции, а должно выполняться лишь в некоторой окрестности точки x0.
Теорема (необходимое условие локального экстремума). Если функция f (x) имеет в точке x0 локальный экстремум и дифференцируема в этой точке, то f’(x0) = 0.
Представленная теорема имеет следующий смысл. Если x1, x2 и x3 – точки локального экстремума и в соответствующих точках графика существуют касательные, то эти касательные параллельны оси Ох.
Такие точки называют точками возможного экстремума. Если точка x0 – точка возможного экстремума, т.е. f’(x0) = 0, то она может и не быть точкой локального максимума (минимума).
Теорема (достаточное условие локального экстремума). Пусть функция f(х) дифференцируема в некоторой окрестности точки х0. Тогда, если f’(x0) > 0 (f (x) < 0) для всех х из (х0 – , x0), а f’(x) < 0 (f’(x) > 0 для всех x из (x0, x0 + ), то в точке x0 функция f(x) имеет локальный максимум (минимум), если же f'(x) во всей – окрестности точки x0 имеет один и тот же знак, то в точке x0 локального экстремума нет.
Пример. Найти максимумы и минимумы следующих функций:
f(x)
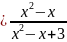 ;
2) f(x)
= (x–2)5.
;
2) f(x)
= (x–2)5.
Решение.
1)
Область определения данной функции –
вся числовая прямая, так как x2–x+3
> 0
при любом x.
Находим производную f’(x)
=
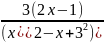 .
Решая уравнение
.
Решая уравнение
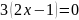 ,
получаем точку возможного экстремума
x
= 1/2. Исследовав знак f’(x)
в окрестности x
= 1/2, получаем,
что в этой точке данная функция имеет
локальный минимум, а f(1/2)
= -1/11 –
минимальное значение функции.
,
получаем точку возможного экстремума
x
= 1/2. Исследовав знак f’(x)
в окрестности x
= 1/2, получаем,
что в этой точке данная функция имеет
локальный минимум, а f(1/2)
= -1/11 –
минимальное значение функции.
Область определения данной функции – вся числовая прямая. Находим производную: f’(x) = 5(x-2)4. Производная обращается в нуль в единственной точке x = 2. Так как f’(x) положительная как слева, так и справа, то данная точка не имеет точек экстремума.
Направление выпуклости и точки перегиба графика функции.
СХЕМА ИССЛЕДОВАНИЯ ГРАФИКА ФУНКЦИИ
Изучение заданной функции и построение ее графика целесообразно проводить в следующим порядке:
Найти область определения функции;
Найти точки пересечения графика функции с осями координат;
Найти точки возможных экстремумов;
Найти критические точки;
С помощью вспомогательного рисунка исследовать знак первой и второй производных. Определить участки возрастания и убывания функции, найти направление выпуклости графика, точки экстремума и точки перегиба;
Построить график.
