2.10.2 Приклади розв’язку задач

Задача 1.

Розв’язати дискретне логарифмічне рівняння виду 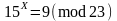методом -Полларда.

Розв’язок.

Обчислюватимемо значення з урахуванням того, що

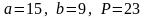
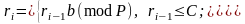
Виберемо С=6 та розрахуємо значення . Результати зведено до таблиці 2.19.

Таблиця 2.19 – Результати розрахунків

І	1	2	3	4	5	6	7
ri	b=9	ab=20	a2b=1	a2b2=9	a3b2=20	a4b2=1	a4b3=9
Ui	0	1	2	2	3	4	4
Vi	1	1	1	2	2	2	3

Аналізуючи значення , ми бачимо, що r₁= r₄= r₇, r₂= r₅, r₃= r₆. Вибравши будь-яку пару та 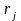, знайдемо пари значень та . Наприклад, для r₃=r₆ маємо при r₃. U_i=2 і V_i=2, для r₆ U_j=4 і V_j=3. Підставивши ці значення в (2.79), маємо

.

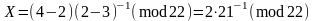Далі знайдемо зворотний елемент y для числа 21 в кільці за модулем 22. Маємо рівняння

.

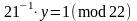Розв’яжемо це рівняння, використовуючи алгоритм Евкліда

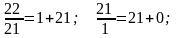
отже 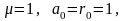тоді

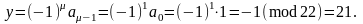
Тому

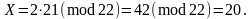
Таким чином, 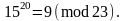Прямим обчисленням перевіряємо пра-вильність розв’язку.

Приклад 2.

Розв’язати дискретне логарифмічне рівняння виду

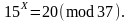
Розв’язок.

Зробимо, використовуючи метод Поліга-Хеллмана. Розкладаємо число

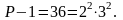
Отже

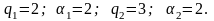
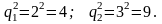
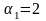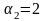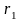Оскільки максимальні значення ступеня залишку і , то згідно з (2.84) та 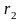лишки матимуть лише два члени. Тому шукатимемо та лишки за модулями 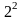та 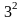відповідно

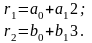
Тепер нам потрібно знайти 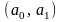та 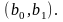Для цього використаємо порівняння (2.94), в результаті отримаємо

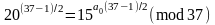або

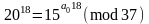
обчисливши ліву частину, маємо

.

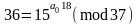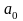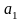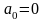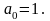Тепер врахуємо, що коефіцієнти та , обчислюються за модулем 2, то або Підставивши ці значення, отримаємо, що Для знаходження використаємо порівняння (2.94), в результаті отримаємо

.

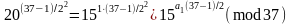Після обчислень маємо

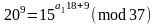
і

.

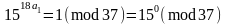Отже

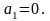
Таким чином,

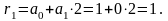
Далі знайдемо аналогічно 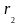, для цього знайдемо 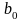та 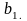Аналогічно як і для маємо

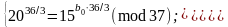
або

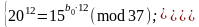
Підставимо в перше порівняння послідовно

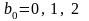(оскільки ).

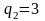За аналогією як і для та , маємо

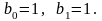
Тому

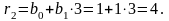
Тепер, знаючи лишки та , можна знайти Х, використовуючи формулу (2.96)

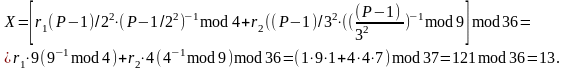
Таким чином,

.

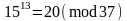Прямою перевіркою підтверджуємо, що 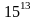дійсно дорівнює 20 за модулем 37.

2.10.3 Задачі для самостійного розв’язання

Задача 1.

Розв’язати порівняння методом -Полларда та Поліга-Хелмана 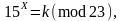де k – номер індивідуального завдання, .

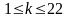Задача 2.

Розв’язати порівня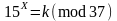ння методом Поліга-Хелмана, де k – номер індивідуального завдання,

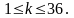
Задача 3.

Визначте складність розв’язку дискретного логарифмічного рівняння, якщо при криптоаналізі використовуються алгоритми -Полларда, Поліга-Хелмана та загального решета числового поля. Значення величини модуля 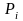визначається як .

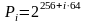Задача 4.

Визначте вартість розв’язку задачі дискретного логарифмічного рівняння для значення модуля, що наведено в задачі 3, якщо потужність криптоаналі-тичної системи складає 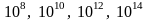та 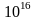опер/с., а вартість одного міпсороку (3,15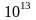 опер/рік) складає 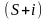грн., S=30, i – номер індивідуального завдання.

Задача 5.

Визначте час розв’язку задачі дискретного логарифмічного рівняння для даних задачі 3, якщо потужність криптоаналітичної системи складає 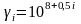опер/с, де і – номер індивідуального завдання.

2.10.4 Контрольні запитання та завдання

1. У яких стандартах використовуються криптографічні перетворення у простих полях Галуа?

2. На чому базується стійкість криптоперетворень в полях Галуа?

3. Які атаки можуть бути реалізовані відносно криптоперетворень в полях Галуа?

4. Які вимоги та чому висувають до модулів перетворень в полях Галуа?

5. Розробіть алгоритм формування загальносистемних параметрів .

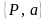6. Поясніть алгоритм виробки загального секрету, що здійснюється з використанням довгострокових ключів.

7. Поясніть алгоритм виробки загального секрету з використанням довгострокових і сеансових ключів.

8. Розробіть алгоритм виробки загального секрету з використанням у абонента А сеансових ключів, а у В – довгострокового.

9. Як виробити із загального секрету ключ або ключі?

10. Поясніть суть алгоритму -Полларда.

11. Оцініть складність розв’язку задачі дискретного логарифмічного рівняння з використанням алгоритму -Полларда.

12. Поясніть суть алгоритму Поліга-Хелмана.

13. Оцініть складність розв’язку задачі дискретного логарифмічного рівняння з використанням загального решета числового поля.

14. Розробіть пропозиції щодо оцінки вартості криптоаналізу з використанням загального решета числового поля.

15. Поясніть сутність алгоритму Поліга-Хелмана.

16. Розробіть методику оцінки складності криптоаналізу за алгоритмом Поліга-Хелмана.