
- •6.4.1 Оцінка автентичності захисту інформації з використанням симетричних алгоритмів. Приклади розв’язку задач та задачі для самостійного розв’язання
- •Ми застосуємо в оцінці відповідне більше, так як не доведено, що в режимі виробки імітоприкладки забезпечується досконала автентичність.
- •1.12 Оцінка автентичності інформації, захищеної з використанням асиметричних алгоритмів. Приклади розв’язку задач та задачі для самостійного розв’язання
- •Відомо також, що імовірність обману можна визначити як
- •1.13 Криптоаналіз rsa та дискретних логарифмiв методом -Поларда. Приклади розв’язку задач та задачі для самостійного розв’язання
- •Задача 1.
- •1.14 Криптоаналiз rsa методом квадратичного решета. Приклади розв’язку задач та задачі для самостійного розв’язання
- •Задача 1.
- •2.7 Аналіз методiв перетворень в перспективних симетричних криптографічних системах. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.7.1 Приклади розв’язку задач
- •2.8 Методи та засоби генерування та розподілу ключів. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.8.1 Приклади розв’язку задач
- •2.9 Симетричні потокові шифри. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.9.1 Приклади розв’язку задач
- •2.10 Стійкість асиметричних криптосистем, що базуються на криптоперетвореннях в простих полях. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.10.2 Приклади розв’язку задач
- •2.11 Стійкість асиметричних криптосистем, що базуються на криптоперетвореннях в групі точок еліптичних кривих. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.11.2 Приклади розв’язку задач
- •Використовуючи формули для додавання точок:
- •При подвоєнні маємо:
- •2.12 Електронні цифрові підписи та їх застосування. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.12.1 Приклади розв’язку задач
- •2.13 Криптографічні протоколи. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.14 Криптографічні протоколи направленого шифрування. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.14.1 Приклади розв’язку задач
- •Побудуйте однораундовий протокол автентифікації, використовуючи rsa криптографічне перетворення, оцініть стійкість протоколу, якщо довжина модуля
- •1) Факторизуємо модуль n і визначаємо прості числа p та q;
- •2.15 Криптографічні протоколи виробки та установки ключів. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.15.1 Приклади розв’язку задач
- •Для умов задачі 6 знайдіть закон розподілу загальних секретів.
- •Задача 10.
- •2.16 Криптографічні протоколи розподілу таємниці. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.16.2 Приклади розв’язку задач
- •2.16.3 Задачі для самостійного розв’язання
- •Задача 5.
- •2.17.1 Приклади розв’язку задач
- •2.17.2 Задачі для самостійного розв’язання
- •14. Оцініть імовірність нав’язування хибного повідомлення для випадку, коли для захисту використовується геш-функція гост-28147-89.
Використовуючи формули для додавання точок:


маємо
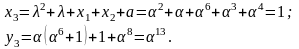
При подвоєнні маємо:

Задача 8.
Знайдіть
вирішення
 ,
,
 .
Мультиплікативний елемент
.
.
Мультиплікативний елемент
.
Розв’язок.
 .
.
Рівнянню відповідають такі елементи:

Будуємо множину відкритих ключів

Таким
чином порядок точки
 n=20.
n=20.
2.11.3 Задачі для самостійного розв’язання
Задача 1.
Дайте
оцінку складності факторизації та
розв’язку дискретного логарифмічного
рівняння в групі точок ЕК, якщо довжина
модулів
та порядок
 .
Визначте значення безпечного часу
,
якщо потужність криптоаналітичної
системи при факторизації
.
Визначте значення безпечного часу
,
якщо потужність криптоаналітичної
системи при факторизації
 гр.оп./с.,
а при розв’язанні дискретного
логарифмічного рівняння
гр.оп./с.,
а при розв’язанні дискретного
логарифмічного рівняння
 оп.
додавання ЕК/с. Проаналізуйте результати
розв’язку задачі та зробіть висновки.
оп.
додавання ЕК/с. Проаналізуйте результати
розв’язку задачі та зробіть висновки.
Задача 2.
Дайте
оцінку складності розв’язку дискретного
логарифмічного рівняння в групі точок
ЕК, якщо довжина модулів та порядок
 .
Визначте значення безпечного часу
,
якщо потужність криптоаналітичної
системи для дискретного логарифмічного
рівняння
гр.оп./с.,
і
оп. додавання ЕК/с. Проаналізуйте
результати розв’язку задачі та зробіть
висновки.
.
Визначте значення безпечного часу
,
якщо потужність криптоаналітичної
системи для дискретного логарифмічного
рівняння
гр.оп./с.,
і
оп. додавання ЕК/с. Проаналізуйте
результати розв’язку задачі та зробіть
висновки.
Задача 3.
Визначте
складність та вартість криптоаналізу
методом повного розкриття для
криптоперетворень в групі точок ЕК над
полем
,
якщо порядок базової точки
 ,
а потужність криптоаналітичної системи
додавань на ЕК/с., а вартість одного
міпсороку складає
грн.
,
а потужність криптоаналітичної системи
додавань на ЕК/с., а вартість одного
міпсороку складає
грн.
Задача 4.
Порівняйте криптоперетворення в кільцях, полях та групі точок ЕК за критерієм складності виконання. Визначте вартість криптоаналізу методом пов-ного розкриття, при якому криптоаналітик знаходить секретний (особистий) ключ абонента, якщо довжини модулів криптоперетворень в кільці, полі та групі точок ЕК відповідно дорівнюють бітів. Потужність криптоаналітичної системи в кільці та полі складає , а в групі точок ЕК . Вартість одного міпсороку складає для криптоперетворень в кіль-ці та полі 30 грн., а в групі точок ЕК 600 грн.
2.11.4 Контрольні запитання та завдання
Назвіть та порівняйте складність основних методів розв’язку дискретних логарифмічних рівнянь в групі точок ЕК.
В чому сутність методу Поларда розв’язку дискретного логарифміч- ного рівняння в групі точок ЕК.
Поясніть алгоритм визначення відкритого ключа.
Які вимоги до загальносистемних параметрів ЕК висуваються з точки зору стійкості?
Які ЕК є слабкими та чому?
Чи залежить стійкість криптоаналізу в групі точок ЕК від виду поля
 ,
чи
?
Якщо так, то чому?
,
чи
?
Якщо так, то чому?Поясніть алгоритм формування послідовності з використанням (2.110) та (2.116).
Поясніть співвідношення (2.115).
Сформуйте умову супернесингулярності ЕК.
Яким чином забезпечується стійкість криптоперетворень в ДСТУ 4145-2002. Дайте оцінку стійкості.
Як можна порівняти складність криптоаналізу в групі точок ЕК та в кільці?
Які параметри (показники) можуть бути використані для оцінки склад- ності та вартості криптоаналізу?
Чи залежить складність криптоаналізу в групі точок ЕК від базису їх подання?
Порівняйте складність виконання криптоаналізу в афінних та проективних координатах.
Запишіть співвідношення для подвоєння та складання в групі точок ЕК в афінному та проективному базисах, поясніть їх.
Оцініть стійкість криптоперетворень в ГОСТ 34.10-2001 та X 9.62.
