Самарский государственный архитектурно - строительный университет

Прохорова О.В.

ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ

Часть 1.

Курс лекций

Самара - 2012

УДК 62-50 (076.5 )

Информационные технологии: Учебное пособие к курсу лекций для студентов специальности Информационные системы и технологии

/ Сост. О.В. Прохорова. - Самара: СГАСУ, 2012. - 129c.

Изложены базовые знания, необходимые для понимания специфики реализации процессов в вычислительной технике и передаче информации по сетям телекоммуникаций. Приведены контрольные вопросы с целью закрепления понимания материала.

Оглавление

1. Модели дискретных структур. Комбинационные схемы 4

1.1. Введение 4

1.2. Функции алгебры логики 8

1.3. Булева алгебра. Функциональная полнота 13

1.4. Минимизация функции алгебры логики 16

1.5. Функции k-значной логики 20

1.6. Основные понятия трехзначной логики 22

1.7. Представление k-значных функций в виде нормальных форм 24

1.8. Двоичное кодирование переменных и функций трехзначной логики 25

1.9. Программная реализация логических функций и автоматов 29

2. Формальные языки и грамматики 33

2.1. Введение в теорию формальных языков и грамматик 33

2.2. Выводы цепочек формального языка. Деревья КСГ 38

2.3. Основные понятия теории формальных языков и грамматик 40

2.4. Приведение грамматик 44

2.4. Операции над языками 49

2.5. Право-линейная и автоматная грамматики 52

3. Теория автоматов 53

3.1. Введение 54

3.2. Способы представления конечных автоматов 57

3.3. Минимизация числа состояний автомата 62

3.4. Использование сети Петри при переходе от грамматики к автомату 66

3.5. Сети Петри. Маркировка 69

3.6. Классификация сетей Петри 74

3.7. Синхронные и асинхронные автоматы 78

3.8. Модели автоматов Мили и Мура 80

3.9. Кодирование автомата 82

3.10. Элементная база синтеза комбинационных схем 89

3.11. Структурный синтез автомата 95

4. Отдельные вопросы теории вычислительных процессов 106

4.1. Автоматы с магазинной памятью 106

4.2. Комбинационные схемы обнаружения ошибок 114

4.3. Пространство сообщений. Коды обнаружения и исправления ошибок 118

Контрольные вопросы 122

Л И Т Е Р А Т У Р А 125

1. Модели дискретных структур. Комбинационные схемы

1.1. Введение

Рассмотрим некоторое устройство с n входами и m выходами. На каждый вход может быть подан произвольный символ из конечного алфавита X=(x₁ .. x _k ), который назовем входным алфавитом. Совокупность символов, поданных на вход устройства образует входные слова P₁ над алфавитом X. Один из символов алфавита X соответствует пустому символу. Если на некоторый вход устройства подается пустой символ, то физически это означает отсутствие какого-либо возбуждения по данному входу. На выходе устройства появляются выходные слова Q_j над алфавитом Y=(y ₁ ... y_l ), который назовем выходным алфавитом.

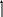
... m выходов

P_i —> Q_j

... n входов

Элементарный такт работы устройства следующий: при появлении на входе устройства входного слова P_i устройство выдает на выходах комбинацию выходных символов, то есть слово Q_j.

Пусть работа устройства полностью определяется лишь входным словом, тогда его работа может быть описана в виде следующей таблицы:

Таблица 1.1

P 1	Qj1
P 2	Qj2
......	.....
P kn	Qjkn

В таблице есть kⁿ строк по числу различных входных слов длиной n над алфавитом X размерности k.

Определение. Устройство, условия работы которого описываются в виде табл. 1.1 называется конечным автоматом без памяти или комбинационной схемой.

Автомат такого типа может рассматриваться как устройство, кодирующее слова над алфавитом X словами над алфавитом Y. Конечный автомат без памяти является наиболее простым логическим устройством дискретного типа.

Зададимся конечным алфавитом S = (S₁ ... S_q ), который называется алфавитом внутренних состояний. Пусть работа устройства полностью описывается входным словом и внутренним состоянием, в котором находится устройство в определенный такт работы, тогда пара (P_i, S_t) однозначно определяет выходное слово и внутреннее состояние, в которое устройство перейдет в следующий такт работы, то есть определяет пару (Q_j, S_h). Работа такого устройства полностью описывается таблицами:

Таблица 1.2

	S1	S2	...	Sq
P1	Qj 1	Qj 2	...	Qj q
P2	Qj q+1	Qj q+2	...	Qj 2q
. . .			...
P kn	...		...	Qj knq

Таблица 1.3

	S1	S2	...	Sq
P1	Sj 1	Sj 2	...	Sj q
P2	Sj q+1	Sj q+2	...	Sj 2q
. . .			...
P kn	...		...	S knq

Табл. 1.2 определенному входному слову P_i и состоянию S_t ставит в соответствие выходное слово Q_jt. Табл.1. 3 определяет внутреннее состояние устройства в следующий такт работы автомата.

Определение. Устройство, работа которого описывается табл.1.2 и

табл. 1.3, называется конечным автоматом с глубиной памяти q.

Конечный автомат с памятью и без нее является устройством детерминированного типа. Описание его работы в виде таблиц есть задание жесткого алгоритма его работы. Но существует более сложный класс автоматов – это автоматы стохастического типа. В автоматах стохастического типа вместо однозначного соответствия P _i -> Q_j или

(P _i , S _t) -> ( Q_j , S_r ) рассматривается лишь вероятность замены P_i на Q_j или (P _i ,S _t) на ( Q_j , S_r ) . Эта вероятность для случая автомата без памяти задается с помощью следующей стохастической матрицы, представленной таблицей:

Таблица 1.4

	Qj1	Qj2	Qj3	...			Qjm
P1	a1 1	a12	a13	...			a1jm
P2	a21	a22	a23	...			a2jm
. . .
P kn	akn1	akn2	a kn3	...			ak njm

Здесь элемент a_{i j} определяет вероятность появления слова Q_j на выходе автомата, если на его вход подано слово P_i . При этом действуют следующие условия:

0  a_{i j}  1 и

Пример.

Рассмотрим процедуру кодирования информации в устройстве оптического сложения двух цветов. Символы алфавита X и Y должны быть закодированы двоичным кодом и принимать значения только 0 и 1. Пусть алфавит X представлен следующим образом: X = (желтый, синий, красный), а алфавит Y представлен: Y = (желтый, синий, красный, зеленый, оранжевый, фиолетовый). В качестве устройства преобразования цвета выберем конечный автомат без памяти с двумя входами и одним выходом. Его работу зададим таблицей (алгоритмом):

Таблица 1.5

желтый + желтый —> желтый желтый + синий —> зеленый синий + желтый —> зеленый желтый + красный —> оранжевый красный + желтый —> оранжевый синий + синий —> синий синий + красный —> фиолетовый красный + синий —> фиолетовый красный + красный —> красный

Автомат в данном случае будет представлять собой устройство для оптического сложения двух цветов. Чтобы построить алгоритм его работы, пронумеруем символы алфавитов X и Y. Для этого первоначально сопоставим каждому цвету целое десятичное число от 0 до 5, а именно: желтому - 0, синему - 1, красному - 2, зеленому - 3, оранжевому - 4, фиолетовому - 5. Результаты кодировки представлены таблицей

0 0 —> 0 0 1 —> 3 1 0 —> 3 0 2 —> 4 2 0 —> 4 1 1 —> 1 1 2 —> 5 2 1 —> 5 2 2 —> 2

000000 —> 000 000001 —> 011 001000 —> 011 000010 —> 100 010000 —> 100 001001 —> 001 001010 —> 101 010001 —> 101 010010 —> 010

Двоичное кодирование алфавита заменяет каждую из 6 десятичных цифр ее эквивалентом в двоичной системе исчисления – кодом в три символа.