Лекция 5. Метрики структурной сложности программ.

Структурная сложность программ определяется:

• числом взаимодействующих компонент;

• числом связей между компонентами;

• сложностью взаимодействия компонент.

При функционировании программы разнообразие ее поведения и разнообразие связей между ее входными и результирующими данными в значительной степени определяется набором маршрутов (чередующихся последовательностей вершин и дуг графа управления), по которым исполняется программа.

Установлено, что сложность программного модуля связана не столько с размером (числом команд) программы, сколько с числом маршрутов ее исполнения и их сложностью.

Для повышения качества программы маршруты возможной обработки данных должны быть тщательно проверены при создании программы и тем самым определяют сложность ее разработки. Данную метрику сложности можно использовать для оценки трудоемкости тестирования и сопровождения модуля, а также для оценки потенциальной надежности его функционирования. Проведенные исследования подтверждают достаточно высокую адекватность использования структурной сложности программ для оценки трудоемкости тестирования, вероятности ненайденных ошибок и затрат на разработку программных модулей в целом.

Все маршруты исполнения программного модуля условно можно разделить на две группы

• вычислительные маршруты

• маршруты принятия логических решений.

Первая группа маршрутов включает в себя маршруты арифметической обработки данных и предназначена для преобразования величин, являющихся квантованными результатами измерения непрерывных физических характеристик (квазинепрерывных переменных).

Для проверки вычислительных маршрутов можно построить достаточно простую стратегию их проверки. Во всем диапазоне входных переменных нужно выбрать несколько характерных точек (предельные значения, значения в точках разрыва и несколько (1-3) промежуточных значений), для которых проверяется работоспособность программы. Предполагается, что в большинстве промежуточных точек программу можно не проверять из-за гладкости значений непрерывных переменных.

Сложность вычислительных маршрутов оценивается следующей формулой:

,

где m – количество маршрутов исполнения программы

l_i – число данных обрабатываемых в i-ом маршруте

_j – число значений обрабатываемых данных j-го типа (2  _j  5)

Расчет сложности программы по данной формуле имеет значительную неопределенность из-за произвола в выборе количества значений _j при изменении входных данных. Поскольку доля вычислительной части во многих сложных программных комплексах обработки информации относительно невелика (общее число арифметических операций не выходит за предел 5–10%), вычислительные маршруты не определяют структурную сложность программ.

Сложность маршрутов принятия логических решений оценивается формулой

,

где p_i – число ветвлений или число проверяемых условий в i-ом маршруте.

Общая сложность программы определяется формулой

,

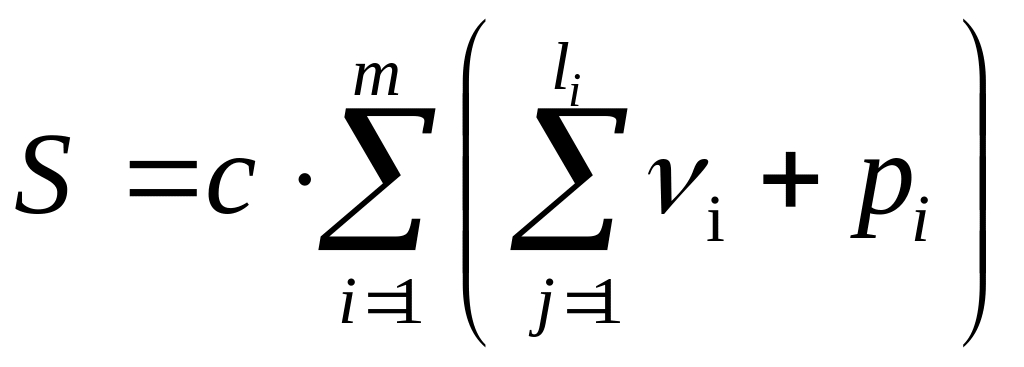где с – некоторый коэффициент пропорциональности, определение которого является сложной задачей.

Выделение маршрутов исполнения программы, минимально необходимых для ее проверки, и оценки структурной сложности могут осуществляться по различным критериям. Наилучшим, по-видимому, является критерий, позволяющий выделить все реальные маршруты исполнения программы при любых сочетаниях исходных данных. При этом формирование маршрутов зависит не только от структуры программы, но и от значений переменных в различные моменты времени. Такое выделение маршрутов трудно формализовать, и оно представляется очень трудоемким для оценки показателей сложности структуры.

Рассмотрим более простые критерии выделения маршрутов, учитывающие только структурные характеристики программных модулей.

Критерий 1. По этому критерию граф программы по управлению должен быть покрыт минимальным набором путей, проходящих через каждый оператор ветвления по каждой дуге. Повторная проверка дуг не оценивается и считается избыточной. При этом в процессе проверки гарантируется выполнение всех передач управления между операторами программы и каждого оператора не менее одного раза.

П оток управления – последовательность выполнения различных модулей и операторов программы.

Граф потока управления – ориентированный граф, моделирующий поток управления программы.

В настоящее время разработаны алгоритмы, позволяющие автоматизировать процесс получения минимального множества маршрутов по этому критерию.

Рассмотрим структурную сложность типичной программы управления, содержащей 100 – 200 команд, граф потока управления которой, представленный на рис.3, содержит 14 вершин, 20 дуг и 3 цикла.

Для полной проверки этой программы по первому критерию достаточно следующих четырех маршрутов:

m1: 1 – 2 – 14

m2: 1 – 3 – 4 – 6 – 8 – 6 – 8 – 14

m3: 1 – 3 – 5 – 7 – 9 – 10 – 11 – 12 – 13 – 14

m4: 1 – 3 – 4 – 5 – 7 – 9 – 10 – 9 – 10 – 11 – 7 – 9 – 10 – 11 – 12 – 14

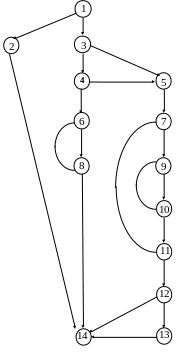
Рис.3

Структурная сложность программы по первому критерию вычисляется следующим образом

m

S =  p_{i ,}

i =1

где p_i – количество вершин ветвления в i-том маршруте без учета последней вершины

m1 1 - 2 - 14 = 1

m2 1 - 3 - 4 - 6 - 8 - 6 - 8 - 14 = 5

m3 1 - 3 - 5 - 7 - 9 - 10 - 11 - 12 - 13 - 14 = 5

m4 1 - 3 - 4 - 5 - 7 - 9 - 10 - 9 - 10 - 11 - 7 - 9 - 10 - 11 - 12 - 14 = 9

20

Таким образом, сложность программы, представленной графом на рис.3, составляет некоторую метрику в 20 единиц.

Недостаток первого критерия: не учитывается комбинаторика сочетания условий на разных участках маршрутов (например, при сочетаниях ветвлений в вершинах 3 и 12).

Критерий 2. Основан на анализе базовых маршрутов в программе, формируемых и оцениваемых на основе цикломатического числа графа потока управления программы (см. работы Т.МcCabe и В.В.Липаева).

Цикломатическое число Z исходного графа программы определяется формулой

Z = Y - N +2*,

где Y – общее число дуг в графе

N – общее число вершин в графе

 – число связных компонент графа.

Число связных компонент графа  равно количеству дуг, необходимых для превращения исходного графа в максимально связный граф.

Максимально связным графом называется граф, у которого любая вершина доступна из любой другой вершины.

Максимально связный граф получается из исходного графа путем замыкания конечных и начальной вершин. Для большинства корректных (не содержащих висячих и тупиковых вершин) графов достаточно одной замыкающей дуги.

Для рассматриваемого графа максимально связанный граф получается путем добавления дуги (14, 1)

Z = Y - N + 2P = 20 - 14 + 21 = 8

Второй критерий (выбранный по цикломатическому числу) требует однократной проверки или тестирования каждого линейно-независимого цикла и каждого линейно-независимого ациклического участка программы. Каждый линейно-независимый ациклический маршрут или цикл отличается от всех остальных хотя бы одной вершиной или дугой, т.е. его структура не может быть полностью образована компонентами других маршрутов.

При использовании второго критерия количество проверяемых маршрутов равно цикломатическому числу.

m1 6 – 8

m2 9 – 10 Линейно-независимые циклические маршруты

m3 7 – 9 – 10 – 11

m 4 1 – 2 – 14 Линейно-

m5 1 – 3 – 4 – 6 – 8 – 14 независимые

m6 1 – 3 – 5 – 7 – 9 – 10 – 11 – 12 – 14 ациклические

m7 1 – 3 – 4 – 5 – 7 – 9 – 10 – 11 – 12 – 13 – 14 маршруты

m8 1 – 3 – 4 – 5 – 7 – 9 – 10 – 11 – 12 – 14

Определение структурной сложности по второму критерию:

m1 6 - 8 = 1

m2 9 - 10 = 1

m3 7 - 9 - 10 – 11 = 2

m4 1 - 2 – 14 = 1

m5 1 - 3 - 4 - 6 - 8 – 14 = 4

m6 1 - 3 - 5 - 7 - 9 - 10 - 11 - 12 – 14 = 5

m7 1 - 3 - 4 - 5 - 7 - 9 - 10 - 11 - 12 – 14 = 6

m8 1 - 3 - 4 - 5 - 7 - 9 - 10 - 11 - 12 - 13 – 14 = 6

26

Для правильно структурированных программ (программ, которые не имеют циклов с несколькими выходами, не имеют переходов внутрь циклов или условных операторов и не имеют принудительных выходов из внутренней части циклов или условных операторов) цикломатическое число Z можно определить путем подсчета числа вершин n_в, в которых происходит ветвление. Тогда

Z = n_в +1

Для рассматриваемого примера Z = 7 + 1 = 8 (ветвления имеют место в вершинах графа 1, 3, 4, 8, 10, 11, 12).

Исследования графов реальных программных модулей с достаточно большим фиксированным числом вершин показали, что:

• Суммарная сложность тестов почти не зависит от детальной структуры графа и в основном определяется числом предикатов – ветвлений графа;

• При неизменном числе вершин в широких графах имеется большее количество маршрутов, чем в узких графах, но маршруты в среднем короткие. В узких графах число маршрутов сокращается по сравнению с широкими, но маршруты становятся длиннее. В результате величина S₂ при изменении структуры графов изменяется меньше, чем цикломатическое число и сильнее коррелирована с числом вершин.

В.В. Липаев показал, что для Z  10 модули корректно проверяемы и число ошибок в таких модулях будет минимальным. Приемлемыми значениями Z считаются 10  Z 30. При Z > 30 устранить ошибки в процессе тестирования практически невозможно.

Для автоматического анализа графов по второму критерию с помощью ЭВМ используются матрицы смежности и достижимости графов.

Матрица смежности – это квадратная матрица, в которой 1 располагается в позиции (i, j), если в графе имеется дуга (i, j).

Для рассматриваемого графа программы матрица смежности имеет вид, показанный в табл.7.

Таблица 7

	1	2	3	4	5	6	7	8	9	100	11	12	13	14
1
2	1
3	1
4			1
5			1	1
6				1				1
7					1						1
8						1
9							1			1
10									1
11										1
12											1
13												1
14		1						1				1	1

Матрицей достижимости называется квадратная матрица, в которой 1 располага-ется в позиции, соответствующей дуге (i, j). Для рассматриваемого графа программы матри-ца достижимости имеет вид, показанный в табл.8.

Таблица 8

	1	2	3	4	5	6	7	8	9	100	11	12	13	14
1
2	1
3	1
4	1		1
5	1		1	1
6	1		1	1		1		1
7	1		1	1	1		1		1	1	1
8	1		1	1		1		1
9	1		1	1	1		1		1	1	1
10	1		1	1	1		1		1	1	1
11	1		1	1	1		1		1	1	1
12	1		1	1	1		1		1	1	1
13	1		1	1	1		1		1	1	1	1
14	1	1	1	1	1	1	1	1	1	1	1	1	1

Матрица достижимости является основной для вычисления маршрутов по второму критерию. Используя ЭВМ, матрицу достижимости можно получить из матрицы смежности путем возведения ее в степень, величина которой равна числу вершин без последней в исходном графе.

С помощью матрицы достижимости можно сравнительно просто выделить циклы, отмечая диагональные элементы, равные 1, и идентичные строк.

Для рассматриваемого примера одинаковыми являются строки 6 и 8, которые имеют 1 на диагонали, следовательно, вершины 6 и 8 образуют цикл. Аналогично можно выделить еще два маршрута с циклами, образованными вершинами 9 и 10 и 7, 9, 10 и 11 соответственно.

Более сильные критерии проверки и определения сложности структуры программы включают требования однократной проверки не только линейно-независимых, но и всех линейно-зависимых циклов и ациклических маршрутов.

Критерий 3. Этот критерий основан на выделении полного состава базовых структур графа программы и заключается в анализе хотя бы один раз каждого из реальных ациклических маршрутов исходного графа программы и каждого цикла, достижимого из всех этих маршрутов.

Если из некоторого ациклического маршрута исходного графа достижимы несколько элементарных циклов, то при тестировании должны исполняться все достижимые циклы.

Для рассматриваемого примера по данному критерию необходимо исполнить 6 ациклических маршрутов и 5 маршрутов, из которых достижимы элементарные циклы.

m1 1 – 2 – 14

m2 1 – 3 – 4 – 6 – 8 – 14

m3 1 – 3 – 5 – 7 – 9 – 10 – 11 – 12 – 14

m4 1 – 3 – 4 – 5 – 7 – 9 – 10 – 11 – 12 – 14

m5 1 – 3 – 5 – 7 – 9 – 10 – 11 – 12 – 13 – 14

m6: 1 – 3 – 4 – 5 – 7 – 9 – 10 – 11 – 12 – 13 – 14

m7 1 – 3 – 4 – 6 – 8 – 6 – 8 – 14

m8: 1 – 3 – 5 – 7 – 9 – 10 – 9 – 10 – 11 – 7 – 9 – 10 – 11 – 12 – 14

m9: 1 – 3 – 4 – 5 – 7 – 9 – 10 – 9 – 10 – 11 – 7 – 9 – 10 – 11 – 12 – 14

m10: 1 – 3 – 5 – 7 – 9 – 10 – 9 – 10 – 11 – 7 – 9 – 10 – 11 – 12 – 13 – 14

m11: 1 – 3 – 4– 5 – 7 – 9 – 10 – 9 – 10 – 11 – 7 – 9 – 10 – 11 – 12 – 13 – 14

Определим структурную сложность заданной программы по третьему критерию:

m1 1 - 2 - 14 = 1

m2 1 - 3 - 4 – 6 – 8 – 14 = 4

m3 1 - 3 - 5 - 7 - 9 - 10 - 11 - 12 - 14 = 5

m4 1 - 3 - 4 - 5 - 7 - 9 - 10 - 11 - 12 – 14 = 6

m5 1 - 3 - 5 - 7 - 9 - 10 - 11 - 12 - 13 - 14 = 5

m6: 1 - 3 - 4 - 5 - 7 - 9 - 10 - 11 - 12 - 13 – 14 = 6

m7 1 - 3 - 4 - 6 - 8 - 6 - 8 - 14 = 5

m8: 1 - 3 - 5 - 7 - 9 - 10 - 9 - 10 - 11 - 7 - 9 - 10 - 11 - 12 – 14 = 8

m9: 1 - 3 - 4 - 5 - 7 - 9 - 10 - 9 - 10 - 11 - 7 - 9 - 10 - 11 - 12 – 14 = 9

m10: 1 - 3 - 5 - 7 - 9 - 10 - 9 - 10 - 11 - 7 - 9 - 10 - 11 - 12 – 13 – 14 = 8

m11: 1 - 3 - 4 - 5 - 7 - 9 - 10 - 9 - 10 - 11 - 7 - 9 - 10 - 11 - 12 – 13 – 14 = 9

S₂ = 1 + 4 + 5 + 6 + 5 + 6 + 5 + 8 + 9 + 8 + 9 = 66

Особенностью четырех последних маршрутов с циклами, так же как соответствующих им ациклических маршрутов, является полный перебор сочетаний ветвлений в вершинах 3 и 12.

Приведенные критерии для оценки сложности программных модулей характеризуют в каждом случае минимально необходимые величины проверок по каждому критерию. Для проверки реальных программ это количество проверок может быть недостаточно (например, циклы желательно проверять на одном-двух промежуточных значениях, а также на максимальном и минимальном количествах исполнения циклов). Оценить достаточность проверок программы значительно труднее, так как при этом, кроме сложности структуры, необходимо анализировать сложность преобразования каждой переменной во всем диапазоне ее изменения и при сочетаниях с другими переменными.