4 Расчет быстровращающихся дисков

Диски постоянной толщины широко применяются в различных конструкциях. К прочности быстровращающихся дисков предъявляются высокие требования, поскольку пи больших числах оборотов они могут получать заметные остаточные деформации, либо полностью разрушаться. Это приводит, как правило, к серьезным авариям. Поскольку на примере дисков постоянной толщины наиболее просто проанализировать влияние отдельных факторов на напряженное состояние, в этой задаче предлагается рассчитать на прочность тонкий диск с закрепленными на его окружности лопатками, вращающимися с постоянной угловой скоростью .

В отношении определения «тонкого диска» заметим, что четких указаний на этот счет в литературе не приводится. Из самых общих соображений можно рекомендовать считать таковыми диски, минимальная толщина которых не превышает половины их радиуса. В этой связи представляется возможным пренебречь перемещениями, перпендикулярными к срединной плоскости диска. Вследствие симметрии напряжения и перемещения будут функциями только расстояния от оси диска.

Рассматриваемая задача имеет статический характер, поскольку движение совершается с постоянной скоростью и, следовательно, центробежные силы инерции постоянны во времени. Используя принцип Даламбера, можно определить действующую нагрузку и соответствующие напряжения в диске.

При решении данной задачи предварительно необходимо определить массу одной лопатки и центробежную силу, вызываемую этой лопаткой.

Зная толщину диска и расстояние между лопатками, интенсивность, периферийной нагрузки (рис. 1.8) определяется следующим образом:

, (1.29)

г де - центробежная сила, вызываемая одной лопаткой, - расстояние между лопатками, - толщина диска.

Рис.1.8

Рассматриваемая задача является осесимметричной, а потому радиальные и цилиндрические сечения диска свободны от касательных напряжений.

Наряженное состояние произвольной частицы показано на рис. 4.1а,б. Общие выражения для радиального и кольцевого напряжений и и радиального перемещения имеют следующий вид:

(1.30)

где E – модуль упругости материала, - коэффициент Пуассона, - удельный вес, - ускорение свободного падения, - угловая скорость, , - постоянные интегрирования, - текущая координата.

Для определения постоянных интегрирования необходимо использовать граничные условия:

а) радиальное напряжение на внешней цилиндрической поверхности равно интенсивности периферийной нагрузки ,

б) в точках диска, примыкающих к ступице, вследствие принятой по условию задачи бесконечно большой ее жесткости, радиальное перемещение равно нулю, т.е.

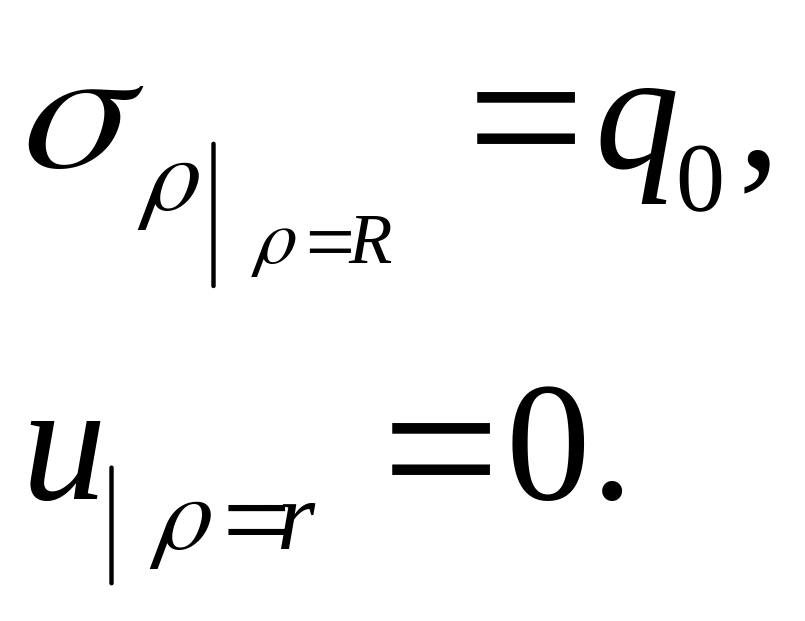(1.31)

Как видно из эпюр напряжений (рис. 4.1), все точки диска находятся в двухосном напряженном состоянии (причем и одинаковы по знаку). Эквивалентные напряжения примем в виде

. (1.32)

Опасной точкой является точка с координатой , т.е. точка диска, примыкающая к ступице.

Из условия прочности

(1.33)

можно получить значение наибольшей допускаемой скорости вращения рассчитываемого диска .

При упругом состоянии диска запасы прочности можно определить двумя способами.

1. По местной прочности. Запас местной прочности

, (1.34)

где - предел длительной прочности материала с учетом температуры на выбранном радиусе диска, - максимальные напряжения ( или ) на данном радиусе диска.

2. По разрушающим оборотам. Запас по оборотам

, (1.35)

где - число оборотов, при котором по радиальному сечению диска кольцевые напряжения достигают предела прочности материала , - число рабочих оборотов диска.