5.5. Условия равновесия частично закрепленного тела

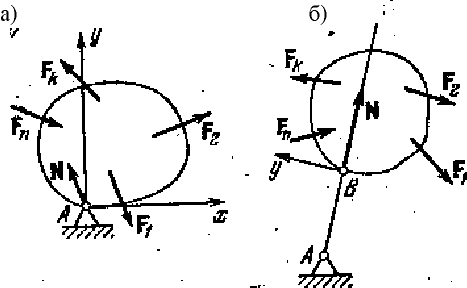
В некоторых случаях приходится рассматривать равновесие частично закрепленных тел, т.е. тел, на которые наложены связи, допускающие некоторое перемещение тела. Два примера такого рода изображены на рис. 5.18 а, б. Очевидно, что

Рис. 5.18.

при произвольной системе активных сил , приложенных к телу, равновесия не будет. Однако возможны и такие случаи, когда равновесие имеет место. Выясним условия, которым должны удовлетворять активные силы, чтобы тело находилось в равновесии. Прежде всего, остановимся на случае твердого тела, имеющего неподвижную ось вращения; к телу приложена система активных сил , расположенная в плоскости, перпендикулярной к оси вращения (рис. 5.18 а). Ось вращения служит связью для рассматриваемого тела; согласно принципу освобождаемости действие связи заменяем реакцией N, приложенной к точке А (предполагаем, что трение отсутствует).

Направление реакции N зависит от характера приложенных к телу сил . Напишем уравнения равновесия в форме (5.18):

Из первых двух уравнений можно найти обе составляющие реакции N. В последнее уравнение N не входит. Это уравнение устанавливает зависимость между активными силами, необходимую для равновесия тела.

Таким образом, для рассматриваемого случая активные силы должны удовлетворять одному уравнению

(5.21)

Обратимся теперь ко второму примеру (рис. 5.16 б), где связью служит стержень. Направление реакции N фиксировано и совпадает с осью стержня. Выбирая систему координат Вху, как указано на рис. 5.18 б, имеем следующие уравнения равновесия:

Первое уравнение служит для определения реакции N. Два остальных уравнения накладывают определенные требования на систему активных сил. Таким образом, для равновесия тела необходимо, чтобы активные силы в данном случае удовлетворяли двум условиям:

(5.22)

Последнее уравнение записано для точки тела В; понятно, что его можно видоизменить, записав его для любой точки оси х.

5.6. Определение натяжения тяжелой подвешенной нити

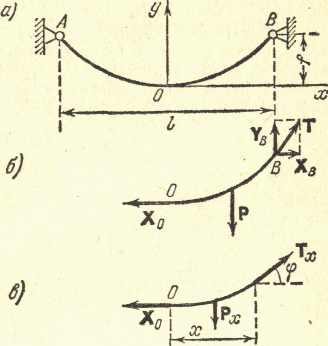
Задача об определении натяжения в подвешенной тяжелой нити (рис. 5.19 а) связана с проблемой прочности тросов или проводов линий электропередачи. Будем считать, что нить идеально гибкая и нерастяжимая и что провисание нити происходит только из-за различия между ее длиной L и расстоянием между опорами l (рис. 5.19 а).

Обозначим через q линейный удельный вес нити. Для пологой кривой можно принять, что вес равномерно распределен не по кривой АОВ, а по ее проекции АВ. Таким образом, общий вес нити будем считать равным .

В соответствии с аксиомой 5 можно рассматривать условия равновесия любой части нити. Рассмотрим, например, правую половину нити; действующие на нее силы изображены на рис. 5.19 б. Заметим, что натяжение в любом сечении нити направлено по касательной к кривой в соответствующем месте (это следует из предположения об идеальной гибкости нити).

Рис. 5.19.

Поэтому в нижней точке нити О, принятой за начало координатной системы, натяжение горизонтально. Обозначив через стрелу провеса (т.е. расстояние по вертикали между нижней точкой и опорами), запишем уравнение моментов относительно точки В

.

Здесь представляет собой вес половины нити. Из этого уравнения находим

; (5.23)

отсюда, между прочим, ясно, что чем меньше стрела провеса нити f, тем больше натяжение .

Из двух уравнений для проекций сил на оси можно найти составляющие натяжения в точке В

, ,

а затем и полное натяжение в точке В

.

Второе слагаемое в сумме под знаком корня значительно меньше единицы, и мы можем воспользоваться приближенной формулой

,

достаточно точной для малых по модулю значений . Тогда будет

. (5.24)

Этот результат определяет наибольшее натяжение нити, которое, впрочем, мало отличается от наименьшего натяжения .

Для вычисления и по найденным формулам необходимо знать стрелу провеса , а для этого требуется располагать уравнением кривой, по которой провиснет нить. С этой целью рассмотрим часть нити, расположенную между началом координат и произвольным сечением с абсциссой х (рис. 5.19 в). Для этой части можно написать следующие уравнения равновесия (для проекций сил на оси х и у):

Здесь  – вес рассматриваемой части нити,  – натяжение на правом конце этой части.

Из первого уравнения можно заключить, что с удалением от нижней точки, т.е. с увеличением угла , натяжение нити возрастает и достигает максимума в точках подвеса.

Исключив из этих уравнений , получим с учетом формулы (5.23)

,

но , и мы приходим к дифференциальному уравнению, определяющему форму нити в положении равновесия:

. (5.25)

Интегрируя его, получаем

.

Постоянную интегрирования найдем из условия, что при ; отсюда следует

.

Таким образом, приближенно установлено, что тяжелая нить в положении равновесия принимает форму параболы. Теперь можно выразить стрелу провеса f через L и . Для этого запишем известное из курса математического анализа выражение длины дуги

и заметим, что для пологой нити . Поэтому . Тогда будем иметь

.

Подставляя сюда выражение (5.25), находим

;

отсюда получаем . (5.26)

Задача 5.8. Определить наименьшее и наибольшее натяжение нити, если вес единицы длины составляет 10 кГ, длина пролета =20 м, а полная длина нити L=21 м.

Прежде всего по формуле (5.26) находим  м.

Наименьшее натяжение нити (в нижней точке) определяется по формуле (5.23):

 кГ.

Наибольшее натяжение (в точках подвеса) находим по формуле (5.24):

 кГ.