19

5.4. Задачи на равновесие системы тел

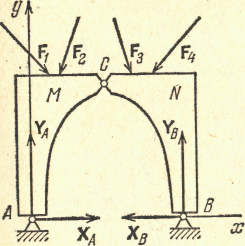
Рассмотрим задачу о нахождении опорных реакций трехшарнирной арки, которая состоит из двух частей, М и N, имеющих шарнирные опоры А и В и соединенных между собой идеальным шарниром С (рис. 5.15 а). Если рассматривать эту систему тел как одно твердое тело (аксиома 5), то будем иметь три уравнения равновесия с четырьмя неизвестными (проекции опорных реакций в точках А и В).

Рис. 5.15.

Тем не менее эта задача статически определенная. Дело в том, что в равновесии находятся два тела М и N, соединенных между собой шарниром С, и можно рассматривать равновесие каждого тела в отдельности. Таким образом, число уравнений равновесия будет равно шести – по три уравнения для каждого тела. Действие тела N на тело М, передаваемое через идеальный шарнир, может быть заменено одной силой, а действие тела М на тело N может быть заменено такой же по модулю силой, но противоположно направленной (аксиома 4).

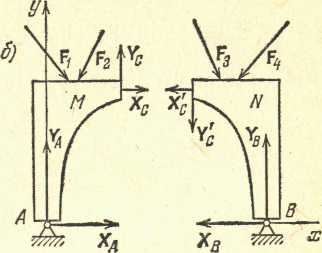
Рассмотрим равновесие каждого тела в отдельности. На рис. 5.15 б указаны силы, приложенные к телам М и N, причем силы и представляют собой составляющие силы, заменяющие собой действие тела N на тело М, а и  – составляющие силы, заменяющие действие тела М на тело N.

Для каждого тела мы можем составить по три уравнения равновесия, т.е. всего шесть уравнений, неизвестных же тоже будет шесть, так как в силу аксиомы 4

, .

Указанный путь решения задачи, конечно, не единственный. Можно, например, составить три уравнения равновесия для тела М, а остальные три – для системы тел М и N, принимая их за одно твердое тело, или составить уравнения равновесия для тела N и уравнения равновесия для системы тел М и N, как для одного твердого тела. Целесообразность применения того или иного способа решения задачи зависит от условий конкретной задачи.

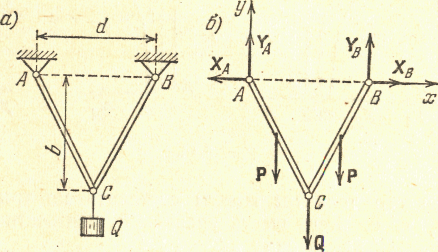
Задача 5.6. Два однородных стержня одинаковой длины соединены шарнирно в точке С и шарнирно закреплены в точках А и В. Вес каждого стержня равен Р. В точке С к системе стержней подвешен груз Q. Расстояние AB=d. Расстояние точки С

Рис. 5.16.

до горизонтальной прямой АВ равно b. Определить реакции шарниров А и В (рис. 5.16 а).

Заменяя действие опор реакциями, рассмотрим сначала равновесие этой системы в целом (рис. 5.16 б). Уравнения равновесия (5.16) в этом случае будут

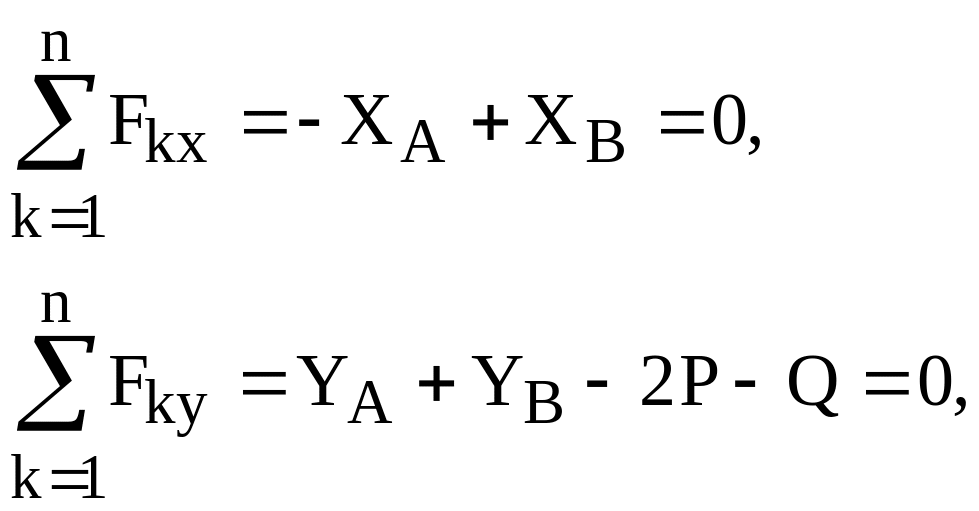
Из этих уравнений находим , .

Для нахождения рассмотрим теперь равновесие левого стержня. Сумма моментов всех сил, приложенных к левому стержню, относительно С должна быть равна нулю, т.е.

;

отсюда .

Задача 5.7. Определить опорные реакции системы, состоящей из двух балок, сочлененных идеальным шарниром, если Р₁=10 т, Р₂=6 т, а=2 м. Конец А балки АС защемлен, конец В балки СВ укреплен в катковой опоре (рис. 5.17 а).

Рассмотрим равновесие каждой балки в отдельности. Мы получаем два твердых тела, на которые действуют реакции внешних связей , , , и попарно равные силы взаимодействия , . Таким образом общее число неизвестных равно шести.

Запишем уравнения равновесия в форме (5.16) для левой балки (рис. 5.17 б):

для правой балки (рис. 5.17 в):

Рис. 5.17.

На основании аксиомы 4 (третьего закона Ньютона) модули сил и , а также сил и , равны между собой, т.е. , . Учитывая эти равенства и решая затем полученную систему уравнений, находим

, ,

 т,  т,  т,  тм.