
- •1 Электрический заряд. Закон кулона.
- •2Напряжённость электростатического поля. Принцип суперпозиции. Силовые линии электростатического поля.
- •3 Потенциал и энергия электростатического поля. Эквипотенциальные поверхности.
- •4Работа в электростатическом поле. Работа по замкнутому контуру. Циркуляция .
- •5 Связь между энергией и силой Кулона, напряжённостью и потенциалом.
- •6 Поток вектора напряжённости электростатического поля. Теорема Гаусса.
- •7 Вычисление напряжённости поля вблизи бесконечной плоскости, нити с поверхностной плотностью заряда σ и линейной плотностью заряда τ.
- •8 Вычисление напряжённости поля вблизи заряженных сферы и шара.
- •9 Электрическое поле в диэлектриках. Полярные и неполярные диэлектрики.
- •10 Поляризация диэлектриков. Вектор поляризации. Дипольный электрический момент
- •11 Поток вектора электрического смещения
- •12Проводник в электростатическом поле
- •13 Электроёмкость заряженных тел, конденсатора
- •14Энергия заряженных тел, конденсаторов
- •15Энергия и плотность энергии электрического поля.
- •16 Электрический ток. Сила тока, плотность тока
- •17 Электродвижущая сила. Работа сторонних сил
- •18 Законы Ома для участка цепи, неоднородного участка цепи, замкнутой системы.
- •19 Правила Кирхгофа
- •20Закон Джоуля-Ленца в интегральной форме
- •21Закон Джоуля-Ленца в интегральной форме и дифференциальной формах
7 Вычисление напряжённости поля вблизи бесконечной плоскости, нити с поверхностной плотностью заряда σ и линейной плотностью заряда τ.
Расчёт напряжённости бесконечной плоскости
Рассмотрим поле, создаваемое бесконечной однородной заряженной плоскостью. Пусть поверхностная плотность заряда плоскости одинакова и равна σ. Представим себе мысленно цилиндр с образующими, перпендикулярными к плоскости, и основанием ΔS, расположенным относительно плоскости симметрично. В силу симметрии E' = E'' = E. Поток вектора напряжённости равен 2EΔS. Применив теорему Гаусса, получим:
![]()
из
которого![]()
![]()
![]()
Расчёт напряжённости бесконечной нити
Рассмотрим поле, создаваемое бесконечной нитью с линейной плотностью заряда, равной λ. Пусть требуется определить напряжённость, создаваемую этим полем на расстоянии R от нити. Возьмём в качестве гауссовой поверхности цилиндр с осью, совпадающей с нитью, радиусом R и высотой Δl. Тогда поток напряжённости через эту поверхность рассчитывается следующим образом:
![]()
В силу симметрии, модуль напряжённости в любой точке поверхности цилиндра будет одинаков. Тогда поток напряжённости через эту поверхность рассчитывается следующим образом:
![]()
Учитывается только площадь боковой поверхности цилиндра, так как поток через основания цилиндра равен нулю. Приравнивая 1 и 2 выражения, получим:
![]()
![]()
8 Вычисление напряжённости поля вблизи заряженных сферы и шара.
Расчет напряженностей для заряженной сферы (поле заряженной сферы).
Пусть имеется:
а)
Полая сфера
![]() или
шар из проводящего материала. В обоих
случаях заряд распределяется по
поверхности по закону Кулона. Тогда по
теореме О.-Г.
или
шар из проводящего материала. В обоих
случаях заряд распределяется по
поверхности по закону Кулона. Тогда по
теореме О.-Г.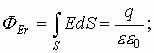
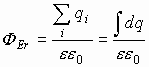 .
.
Приравняем интегралы
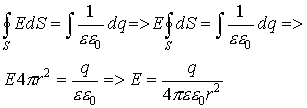
Аналогичным
способом рассуждая, полный поток вектора
![]() через
сферу любого радиуса r определится как:
через
сферу любого радиуса r определится как: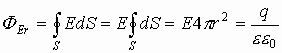
Окончательно
получаем напряженность в любой точке
пространства, расположенной вдали от
заряженной полой сферы: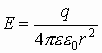
б)
Если
![]()
Каждый отдельно взятый заряд на поверхности сферы дает силовую линию, которая пересекает сферу радиуса r дважды (со знаком “+” и со знаком “-”, т.е. входящий и выходящий), таким образом результирующее количество векторов Е, пересекающих эту сферу, равно нулю. То есть электрическое поле внутри полой сферы отсутствует.
в) Поле сферы с зарядом, равномерно распределенным по объему.
По закону Кулона (взаимное отталкивание зарядов) в однородном проводящем теле заряды распределяются по поверхности. Поэтому возьмем искусственный случай смеси проводящих элементов в непроводящей массе.
Рассмотрим
случай (r > R): Аналогично рассуждая,
поток вектора Е через сферу радиуса r
определится как: ;
И
вновь получим:
;
И
вновь получим: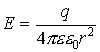 -
напряженность вдали от сплошной
заряженной сферы.
-
напряженность вдали от сплошной
заряженной сферы.
Рассмотрим случай (r < R):
По
теореме Гаусса поток вектора Е состоит
из двух потоков
![]() ,
где
,
где
![]() -
поток векторов, обусловленный внешним
кольцом зарядов относительно сферы
радиуса
-
поток векторов, обусловленный внешним
кольцом зарядов относительно сферы
радиуса
![]() ,
по определению он
0 (см. пр. тему).
,
по определению он
0 (см. пр. тему).
![]() -
поток векторов Е внутренних зарядов
относительно сферы радиуса r:
-
поток векторов Е внутренних зарядов
относительно сферы радиуса r: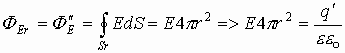 ,
где
,
где
![]() -
заряд внутри сферы r.
-
заряд внутри сферы r.
Вводится
понятие объемной плотности заряда
, т.е. количество заряда в единице объёма,
тогда количество заряда внутри сферы
r определится как: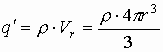 ,
где
- объемная плотность заряда.
,
где
- объемная плотность заряда.
По
определению: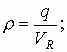 а
также:
а
также: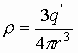
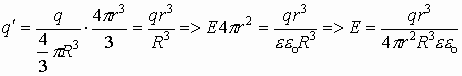
Окончательно
получаем, что величина напряженности
в любой точке пространства внутри
однородно заряженной сферы: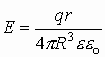 .
.
