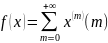4.Определение обобщенной функции. Примеры обобщенных функций.

Пусть пространство финитных функций.

Опр. Лин. непрерыв. функционал на пространстве будем наз-ть обобщённой функцией(на числовой оси ).

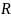Множество всех обобщённых функций, в силу данного выше определения, образует сопряженное множество 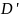к пространству финитных функций .

Если – обобщённая функция и 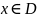, то число 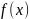называют значением обобщённой функции f на финитной функции x.

Отметим, что часто вместо в математической литературе применяются обозначения <f,x> или <f(t),x(t)>, а в техническо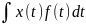й - или .

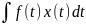Для того чтобы линейный функционал на пространстве D был бы обобщённый функцией, необходимо и достаточно выполнения одного из следующих условий:

1. Для любой последовательности ( 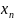) сходящейся к нулю в пространстве D числовая последовательность (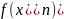 ) сходится к нулю.

2. Функционал ограничен.

3. Для любого натурального числа n функционал непрерывен на пространстве , то есть выполняется следующее условие:

. Если в условии (3) взять m,не зависящее от n, что эквивалентно условию 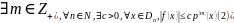, то функционал f наз-ся обобщённой функцией конечного порядка сингулярности, причём наименьшее m, при котором выполняется (2), наз-ся порядком сингулярности обобщённой функции f. Обобщённые функции, не являющиеся обобщёнными функциями конечного порядка сингулярности, наз-т обобщёнными функциями бесконечного порядка сингулярности.

Функция, определённая на числовой оси, будет наз-ся обычной, если она интегрируема по Лебегу на любом конечном интервале числовой оси.

Пусть f- обычная функция. Сопоставим ей функционал 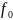на пространстве D по следующей формуле: 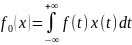( ) (3).

Так как f- обычная функция, а функция x финитна, то интеграл в правой части равенства (3) существует и конечен.

Линейность функционала следует из линейности интеграла.

Докажем, что функционал непрерывен. Пусть 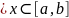. Из определяющего равенства (3) имеем 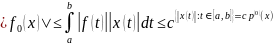, где ради краткости введено обозначение .

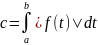Из получ. нерав-ва следует, что -обобщ. ф-ция нулевого порядка сингулярности.Т.о., каждой обычной функции мы сопоставили обобщённую функцию, причём нулевого порядка сингулярности. Такие обобщённый функции называют регулярными. В этом случае говорят, что регулярная обобщённая функция порождена обычной функцией f. Обобщённые функции, не являющиеся регулярными, наз-ся сингулярными обобщёнными функциями.

Примеры не регулярных обобщённых функций:

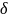1. -функция. Обобщённая функция , называемая дельта-функцией, или дельта-функцией Дирака, которая определяется равенством

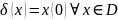
2. Смещенная -функция. Зафиксируем 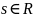и определим обобщённую функцию 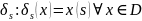. обобщённая 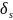называется смещенной -функцией.

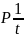3. Обобщённая функция . Функция 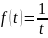не явл-ся обычной функцией, так как она не интегрируема в окрестности нуля. Однако можно определить обобщённую функцию, обозначаемую , следующим образом: 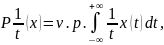где v.p.- означает главное значение в смысле Коши рассм-го интеграла.

4. Обобщённая функция

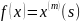
5. Обобщённая функция