Уравнение плоскости, проходящей через три точки

Через три точки, не лежащие на одной прямой, можно провести единственную плоскость.

Уравнение плоскости, проходящей через три данные точки , , : .

Уравнение плоскости в отрезках

- уравнение плоскости в отрезках.

Следует запомнить, что a, b, c – величины отрезков, отсекаемых плоскостью на координатных осях (считая каждый от начала координат).

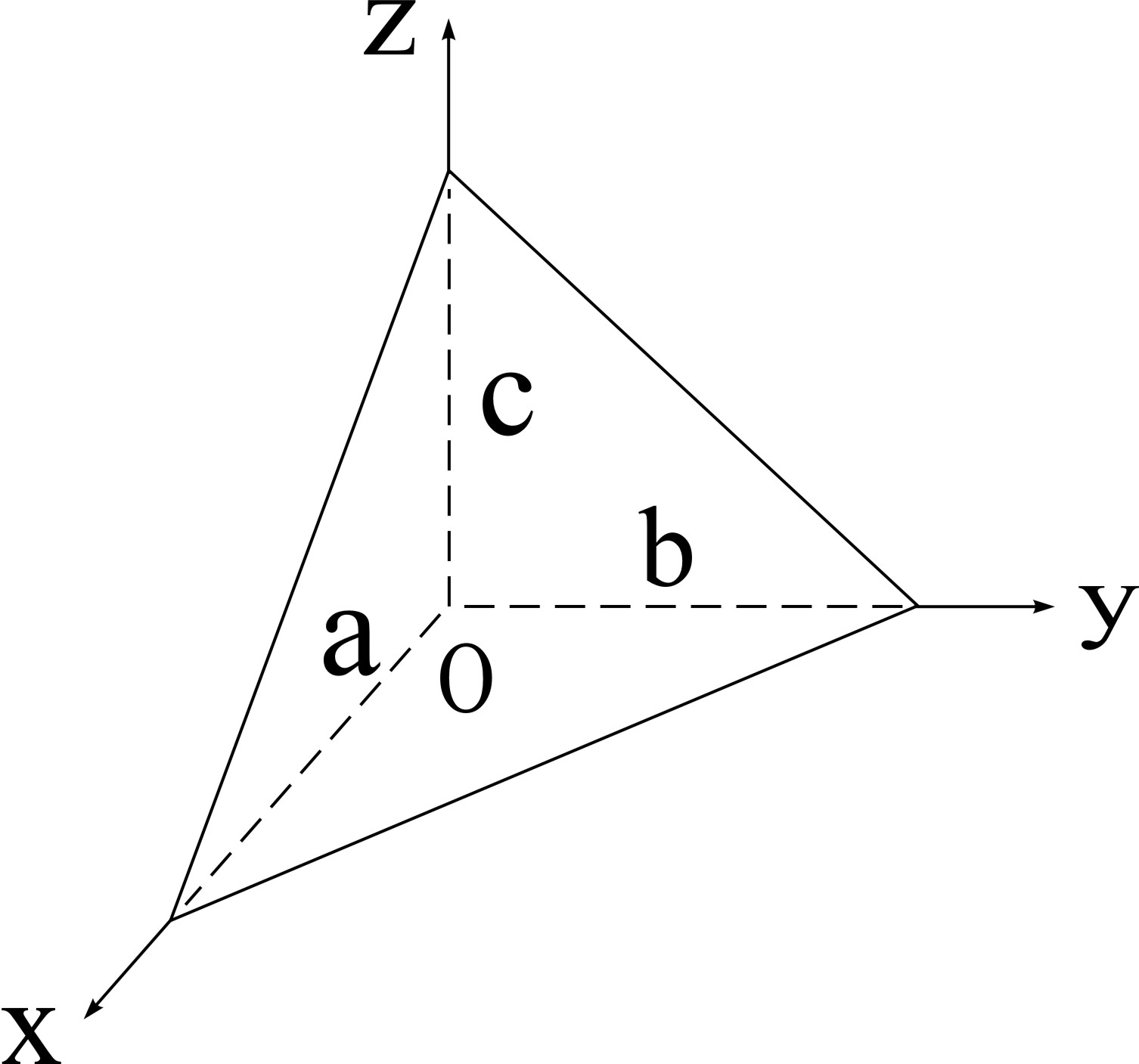
Рис. 1

Замечание 1.

К виду уравнения в отрезках можно привести уравнение всякой плоскости за исключением случая , т. е. плоскости, проходящей через начало координат.

Замечание 2.

Уравнение плоскости в отрезках удобно использовать при построении плоскости.

Нормальное уравнение плоскости

- нормальное уравнение плоскости.

Положение вполне определяется заданием единичного вектора , имеющего направление перпендикуляра, опущенного на плоскость из начала координат, и длиной p этого перпендикуляра.

p – длина перпендикуляра, опущенного из начала координат на плоскость;

, , - направляющие косинусы перпендикуляра, проведенного из начала координат к данной плоскости.

Особенности нормального уравнения плоскости:

1. сумма квадратов коэффициентов при текущих координатах равна единице;

2. свободный член его .

Для приведения общего уравнения плоскости к нормальному виду следует умножить все его члены на нормирующий множитель , где знак перед радикалом противоположен знаку свободного члена D в общем уравнении плоскости.

Уравнение плоскости, проходящей через данную точку

перпендикулярно данному вектору.

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору : .

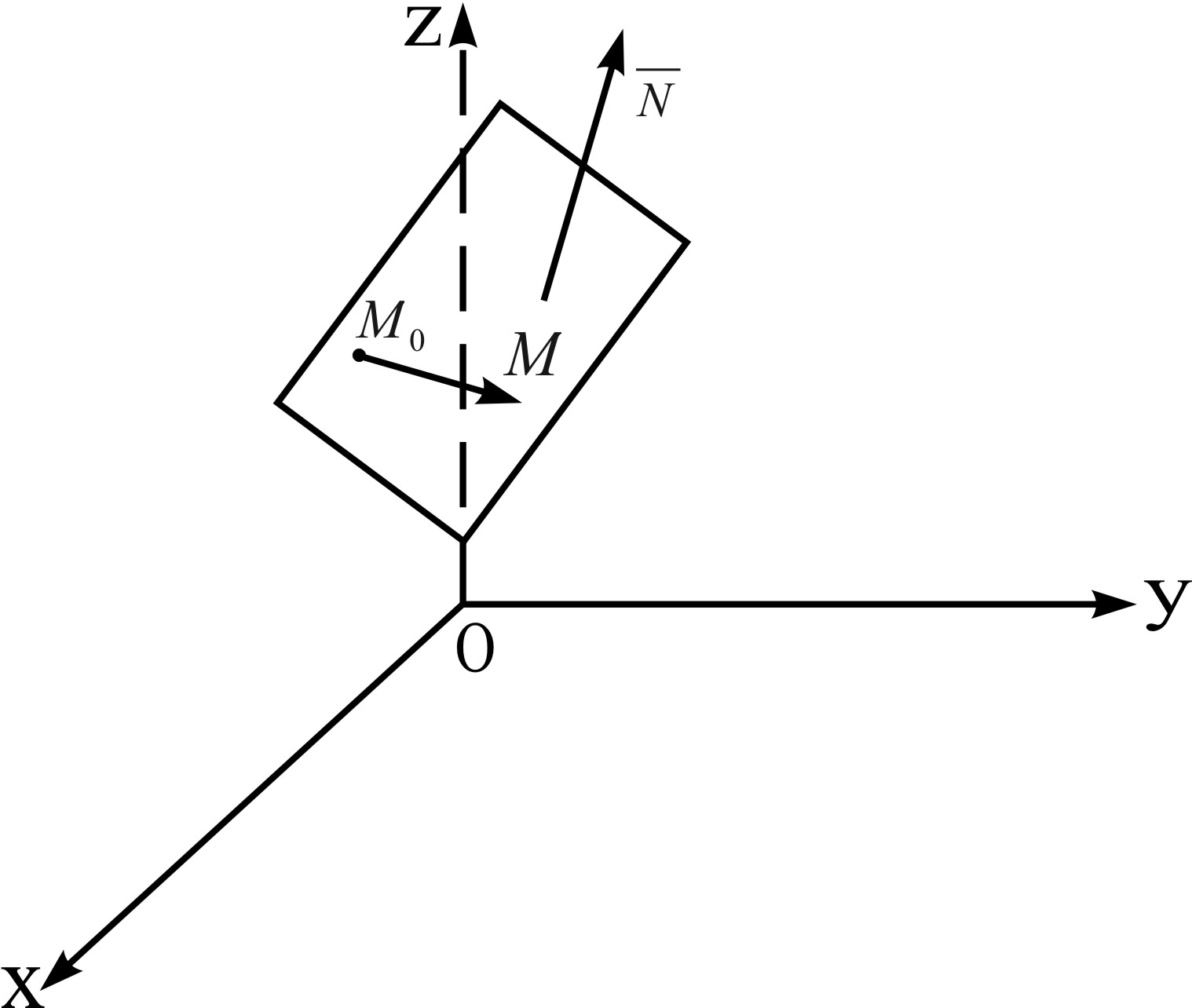
Рис. 2

- нормальный вектор плоскости – каждый (не равный нулю) вектор, перпендикулярный плоскости.

За нормальный вектор плоскости можно принять любой вектор, перпендикулярный плоскости. Ни его длина, ни точка приложения не играют роли.

Плоскость. Основные задачи.

Угол между плоскостями

Пусть заданы две плоскости , и , . Тогда Угол между плоскостями (Рис. 3)

определяется по формуле .

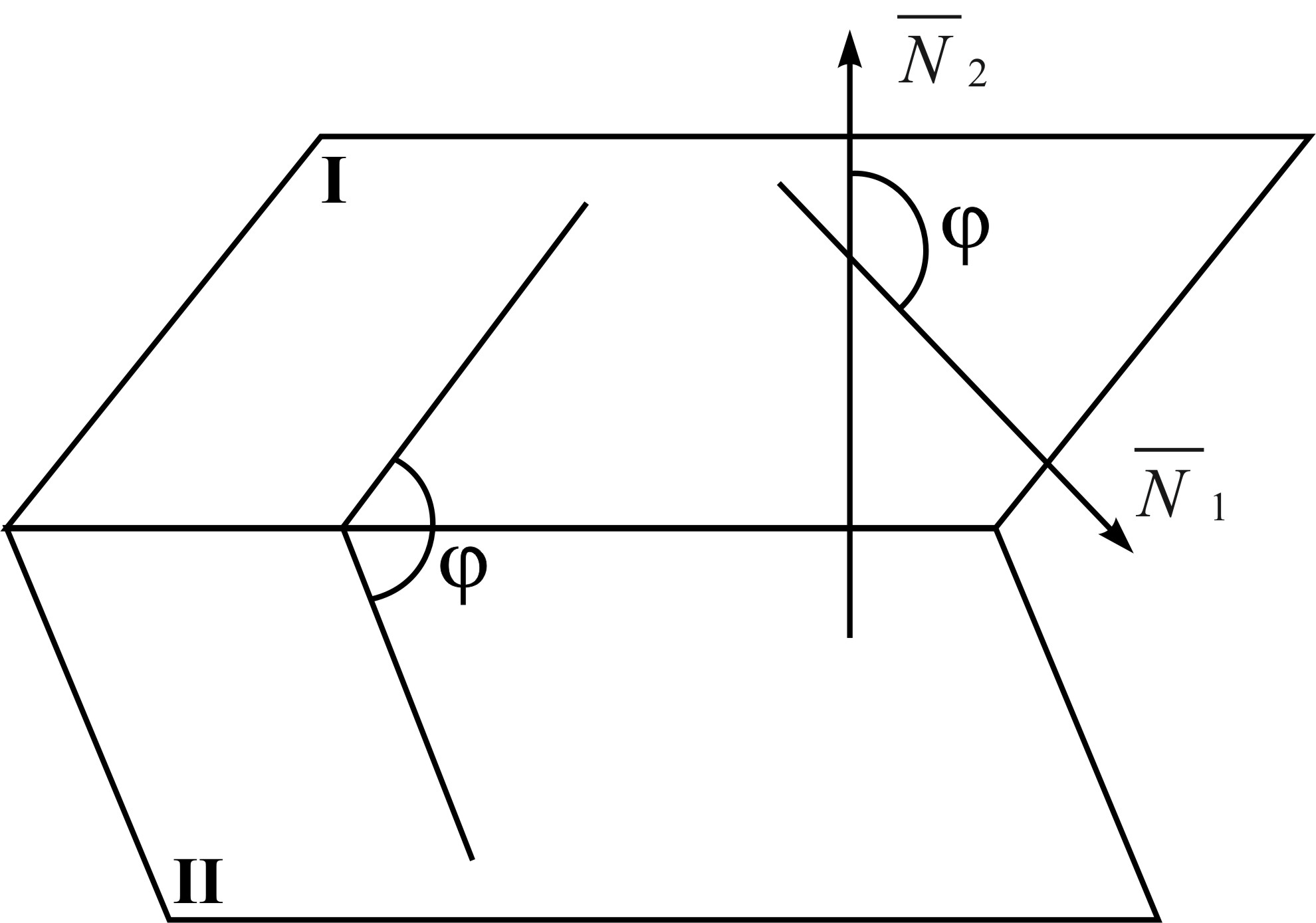
Рис. 3

Определение: Углом между двумя плоскостями будем называть любой из двух смежных двугранных углов, образованных этими плоскостями.

Замечание 1.

Нахождение угла между двумя плоскостями сводится к нахождению угла между нормальными векторами данных плоскостей: .

Замечание 2.

В формуле можно брать любой знак (+ или -), что соответствует выбору одного из двух смежных двугранных углов.

Замечание.

Условие параллельности двух плоскостей

- условие параллельности двух плоскостей.

Замечание. Если , то плоскости совпадают.

Условие перпендикулярности двух плоскостей

- условие перпендикулярности двух плоскостей.

Плоскости перпендикулярны, если скалярное произведение нормальных векторов и равно нулю.

Точка пересечения трех плоскостей

Нахождение точки пересечения трех плоскостей сводится к решению системы трех линейных уравнений.

- необходимое и достаточное условие того, что три плоскости:

, ,

имеют только одну общую точку.

Расстояние от точки до плоскости

Расстояние от точки до плоскости определяется по формуле: .

Задачи

Задача 1. Написать уравнение плоскости, параллельной оси и проходящей через точки и .

Решение

Поскольку плоскость параллельна оси , ее уравнение имеет вид . Подставляя в это уравнение координаты точек M и N, имеем, откуда , . Следовательно, искомое уравнение записывается в виде или .

Задача 2. Написать уравнение плоскости, проходящей через ось , и точку .

Решение

Так как плоскость проходит через ось , то ее уравнение имеет вид .

Подставляя в это уравнение координаты точки M, получим или .

Таким образом, имеем , т. е. , откуда получаем искомое уравнение или .

Задача 3. Даны точки и . Составить уравнение плоскости, проходящей через точку и перпендикулярной вектору .

Решение

Найдем координаты нормального вектора . Имеем . Подставляя в уравнение (4) значения , , , , , , получим искомое уравнение: или .

Задача 4. На оси найти точку, равноудаленную от двух плоскостей: и .

Решение

Так как точка расположена на оси , следовательно, ее координаты . На основании формулы (10) имеем: , , следовательно, , откуда , .

Решая каждое из полученных уравнений, находим, что , , , .

Задача 5. Одна из граней прямоугольного параллелепипеда лежит в плоскости . Найти уравнение плоскости, в которой лежит перпендикулярная ей грань, если известно, что она проходит через точки и .

Решение

Приведем два способа решения задачи.

Способ первый

Запишем уравнение искомой плоскости в виде .

Так как плоскости перпендикулярны, то . Искомая плоскость проходит через точки и , следовательно, получаем второе условие .

.

Откуда , .

Искомое уравнение плоскости записывается в виде или .

Способ второй

Запишем уравнение искомой плоскости в виде , где

- координаты любой из данных точек или а - нормальный вектор искомой плоскости.

Значит, и = - нормальный вектор данной плоскости.

Следовательно, нормальным вектором искомой плоскости можем быть вектор или . Искомое уравнение плоскости или .