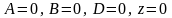- •Аналитическая геометрия Лекция №9. Система координат на плоскости. Метод координат. Прямая на плоскости. Система координат на плоскости. Метод координат.
- •Основные приложения метода координат на плоскости Расстояние между двумя точками
- •Деление отрезка в данном отношении
- •Площадь треугольника
- •Прямая на плоскости
- •Уравнения прямой на плоскости Общее уравнение прямой
- •Уравнение прямой, проходящей через данную точку
- •Уравнение прямой, проходящей через две точки
- •Угол между прямыми
- •Расстояние от точки до прямой
- •Уравнение плоскости, проходящей через три точки
- •Уравнение плоскости в отрезках
- •Нормальное уравнение плоскости
Угол между прямыми
Если две прямые заданы уравнениями с
угловым коэффициентом
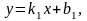
 ,
то угол между ними
(Рис. 6) определяется по формуле:
,
то угол между ними
(Рис. 6) определяется по формуле:
 .
.
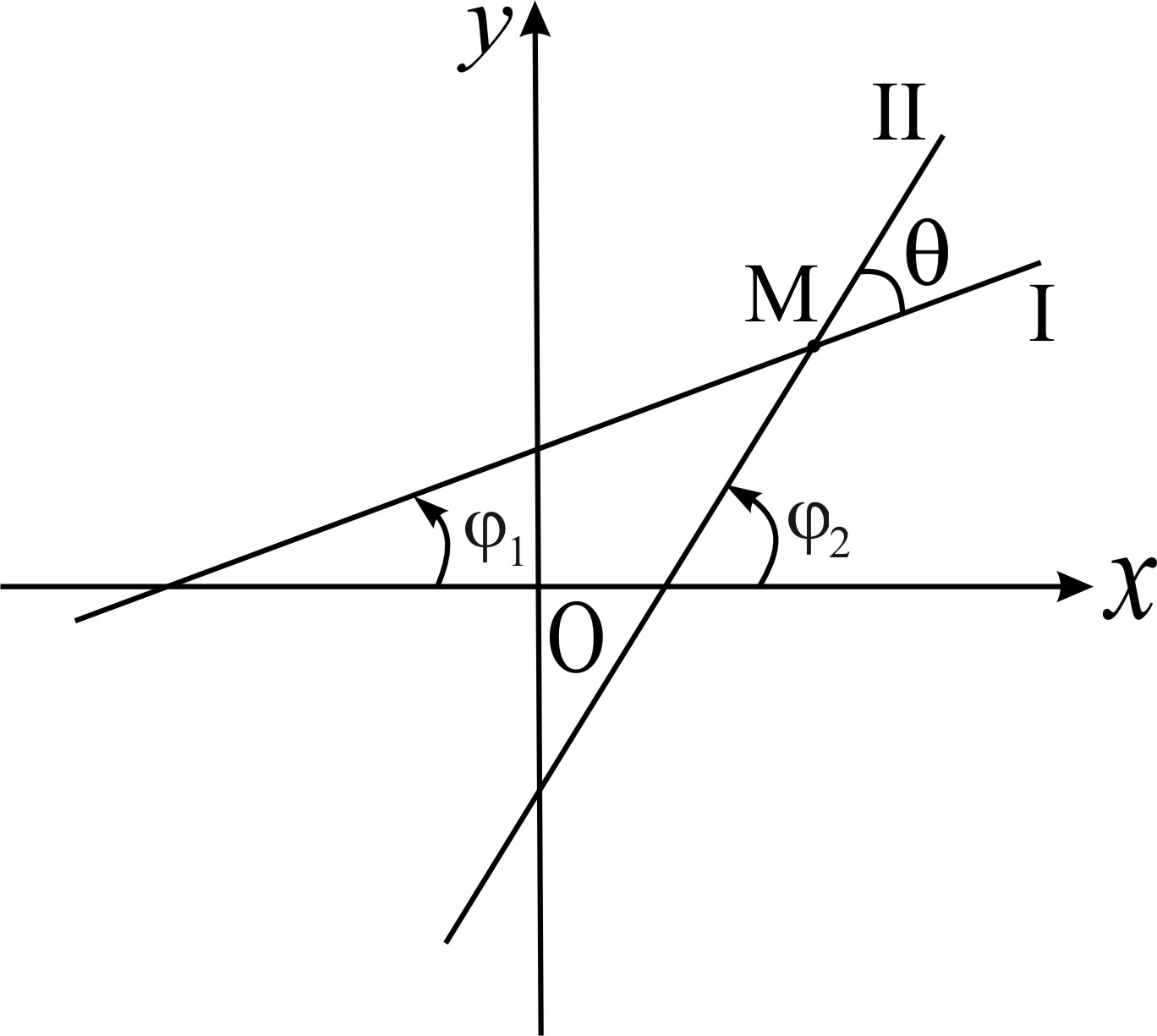
Рис.6
Если уравнения
прямых заданы в общем виде:
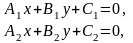 то угол между ними определяется по
формуле
то угол между ними определяется по
формуле
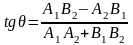 .
.
Пусть две прямые заданы уравнениями общего вида .
Возможны три случая:
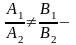 прямые
пересекаются;
прямые
пересекаются;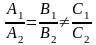 -прямые
параллельны;
-прямые
параллельны;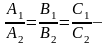 прямые
совпадают.
прямые
совпадают.
Следует запомнить.
Если прямые пересекаются, т.е. имеют одну общую точку, то координаты этой точки должны удовлетворять обоим уравнениям.
Следовательно, для нахождения координат точки пересечения прямых нужно решить совместно их уравнения.
Если две прямые заданы уравнениями с
угловым коэффициентом
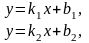 ,
то прямые:
,
то прямые:
параллельны, если
 ,
,
 .
.перпендикулярны, если
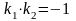 .
.
Расстояние от точки до прямой
Определение: Расстояние от точки
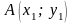 до прямой
до прямой
 есть длина перпендикуляра, опущенного
из этой точки на прямую.
есть длина перпендикуляра, опущенного
из этой точки на прямую.
Расстояние от точки
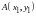 до прямой
до прямой
 :
: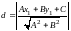 .
.
Задачи
Задача
1. Составить уравнение прямой,
которая отсекает на отрицательной
полуоси
отрезок,
равный 3 единицам, и образует с осью
угол
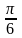 .
.
Решение
Прямая
пересекает ось
в точке
 и имеет угловой коэффициент
и имеет угловой коэффициент
 .
Полагая в уравнении (4)
.
Полагая в уравнении (4)
 и
и
 получим искомое уравнение:
получим искомое уравнение:
 или
или
 .
.
Задача
2. Составить уравнение прямой,
проходящей через точку А(2; 5) и отсекающей
на оси ординат отрезок
 .
.
Решение
Будем искать уравнение прямой в виде .
Согласно
условию задачи
.
Прямая проходит через точку А (2; 5),
следовательно, координаты точки
удовлетворяют данному уравнению.
Получаем
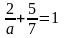 ,
,
 .
.
Искомое
уравнение прямой
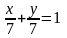 или
или
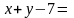 0.
0.
Задача
3. Найти уравнение прямой, которая
проходит через точку
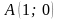 и удовлетворяет условию:
и удовлетворяет условию:
параллельна прямой

перпендикулярна прямой
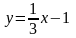
Решение
Угловой коэффициент
 прямой линии, для которой нужно составить
уравнение, равен угловому коэффициенту
прямой линии, для которой нужно составить
уравнение, равен угловому коэффициенту
 данной прямой в силу условия параллельности
этих прямых. Таким образом, полагая в
уравнении (7)
данной прямой в силу условия параллельности
этих прямых. Таким образом, полагая в
уравнении (7)
 ,
,
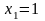 ,
,
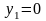 ,
получим искомое уравнение
,
получим искомое уравнение
 или
или
 .
.Искомый угловой коэффициент обозначим через
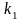 .
Угловой коэффициент данной прямой
.
Угловой коэффициент данной прямой
 ,
как видно из ее уравнения, равен
,
как видно из ее уравнения, равен
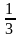 .
Условие перпендикулярности
нам дает:
.
Условие перпендикулярности
нам дает:
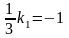 ,
откуда
,
откуда
 .
Таким образом, искомое уравнение
.
Таким образом, искомое уравнение
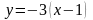 или
или
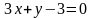 .
.
Задача
4. Найти расстояние между параллельными
прямыми
 и
и
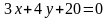 .
.
Решение
Искомое
расстояние найдем как расстояние от
произвольной точки первой прямой до
второй прямой. Возьмем на первой прямой
произвольную точку, например, точку с
абсциссой
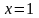 .
Ее ордината
.
Ее ордината
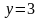 .
Итак, на первой прямой выбрана точка
.
Итак, на первой прямой выбрана точка
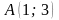 .
Найдем теперь расстояние от этой точки
до второй прямой по формуле
.
Найдем теперь расстояние от этой точки
до второй прямой по формуле
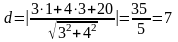 .
.
Лекция №10. Плоскость.
Определение: Всякое уравнение первой степени относительно текущих координат определяет в пространстве плоскость.
Уравнения плоскости в пространстве
Общее уравнение плоскости
Уравнение первой степени с тремя
неизвестными :
:
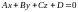 - общее уравнение плоскости
- общее уравнение плоскости
Частные случаи общего уравнения плоскости
Если отсутствует член с одной из координат, то плоскость параллельна соответствующей оси координат. |
|
|
|
плоскость проходит через начало координат |
|
|
плоскость параллельна оси |
|
|
плоскость параллельна оси |
|
|
плоскость параллельна оси
|
Если одновременно отсутствует свободный член и член с одной из координат, то плоскость проходит через соответствующую ось. |
|
|
|
плоскость проходит через ось |
|
|
плоскость проходит через ось |
|
|
плоскость проходит через ось |
Если отсутствуют члены с двумя координатами, то плоскость параллельна той координатной плоскости, которая содержит соответствующие оси. |
|
|
|
плоскость параллельна плоскости
|
|
|
плоскость параллельна плоскости
|
|
плоскость параллельна плоскости
|
Если отсутствуют члены с двумя координатами и свободный член, то плоскость совпадает с одной из координатных плоскостей. |
|
|
плоскость совпадает с плоскостью |
|
|
плоскость совпадает с плоскостью |
|
|
плоскость совпадает с плоскостью . |
Если отсутствуют все члены с координатами, а свободный член отличен от нуля, то уравнение смысла не имеет. |
|

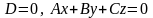
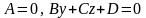


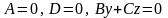


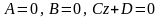
 (перпендикулярна оси
)
(перпендикулярна оси
)
 (перпендикулярна оси
)
(перпендикулярна оси
)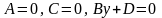
 (перпендикулярна оси
)
(перпендикулярна оси
)