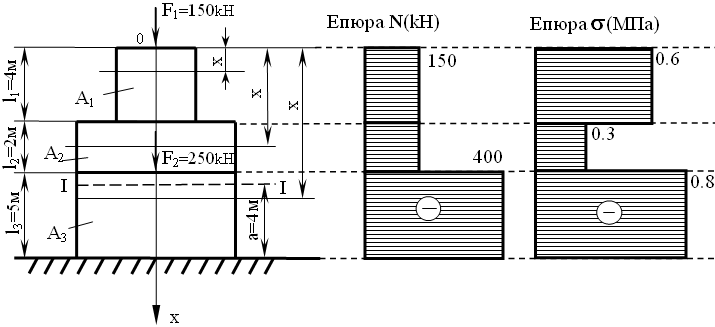
Розв’язання задачі без урахування власної ваги.

Брус, який розглядається, є статично визначеним і має три ділянки. При визначенні і розрахунок ведемо від вільного кінця (у цьому разі реакцію R визначити не потрібно), тобто визначаємо та по силах, що розташовані вище розглянутих перерізів.

а) б) в)

Рис.1.1

а) б) в)

Рис. 1.2

Згідно з рис. 1.2 а, б, в визначаємо і .

Ділянка І:

,

,

Ділянка II:

,

Ділянка Ш:

,

,

За отриманими даними будуємо епюри і (рис. 1.1 б,в).

Небезпечними будуть перерізи, які належать ділянці Ш. Умова міцності (1.6) для цих перерізів виконується, тому що

.

Повна деформація бруса

,

де , , – деформації відповідних ділянок бруса.

Згідно з (1.2)

,

,

,

.

Переміщення перерізу I-I відносно затиснення

.

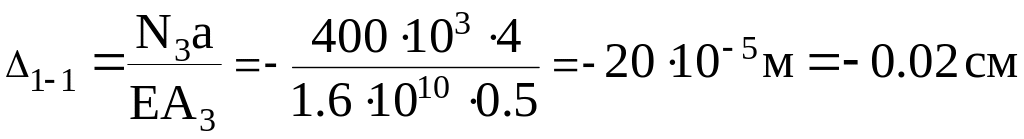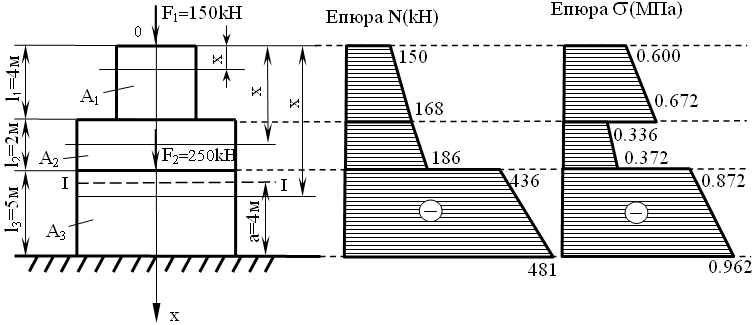
Розв’язання задачі з урахуванням власної ваги.

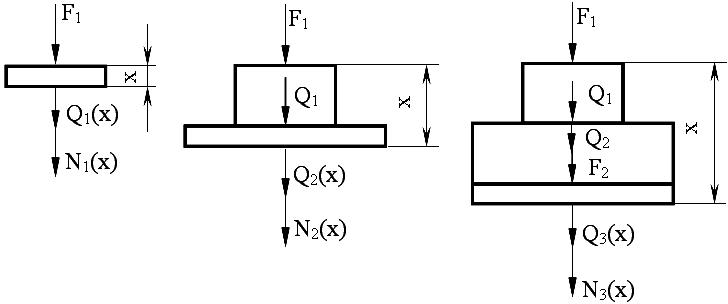
Згідно з рис. 1.4 а, б, в визначаємо і .

а) б) в)

Рис. 1.3

а) б) в)

Рис. 1.4

Ділянка І:

,

, ,

,

.

При x = 0:

,

При x = 4м:

,

Другий член у виразі для N₁ являє собою власну вагу ділянки 1 Q₁=18кH.

Ділянка ІІ:

,

, ,

,

.

При x = 4м:

,

При x = 6м:

.

Третій член тут дорівнює власній вазі другої ділянки Q₂=18кH.

.

Ділянка ІІІ:

,

,

,

, .

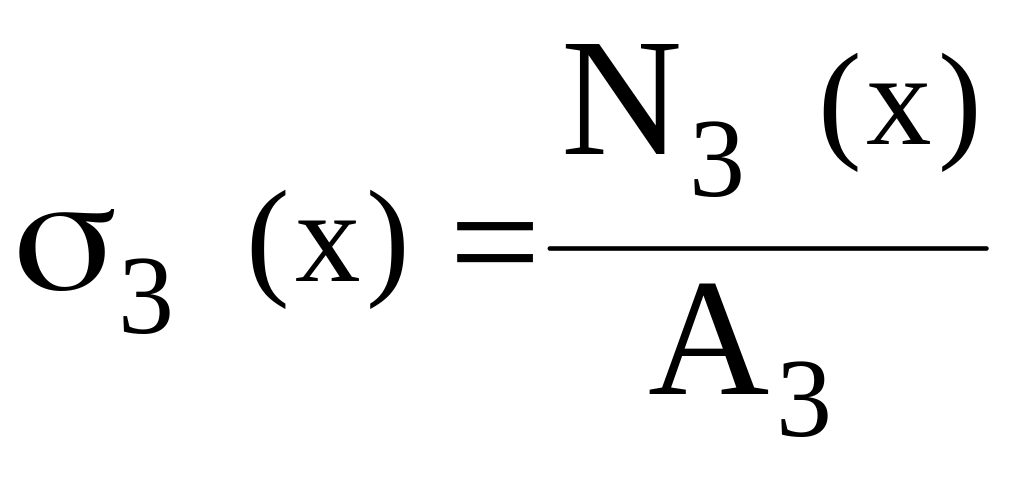При х = 6 м;

,

.

При x=11м:

.

П’ятий член дорівнює власній вазі третьої ділянки Q₃=45кH.

.

За отриманими даними будуємо епюри N і σ (рис. 1,3 б,в).

Небезпечним буде нижній переріз бруса. Умова міцності (1.6) для цього перерізу виконується, тому що

.

Повна деформація бруса

,

де , , – деформації відповідних ділянок бруса.

Згідно з (1.4)

.

Переміщення перерізу 1-1, який належить ділянці Ш:

,

де

Отримуємо

За допомогою формули (1.11) доберемо найбільш економічні розміри квадратного поперечного перерізу кожної ділянки бруса.

Для ділянки 1

.

Тоді сторона квадратного перерізу

.

Для ділянки П

Для ділянки Ш

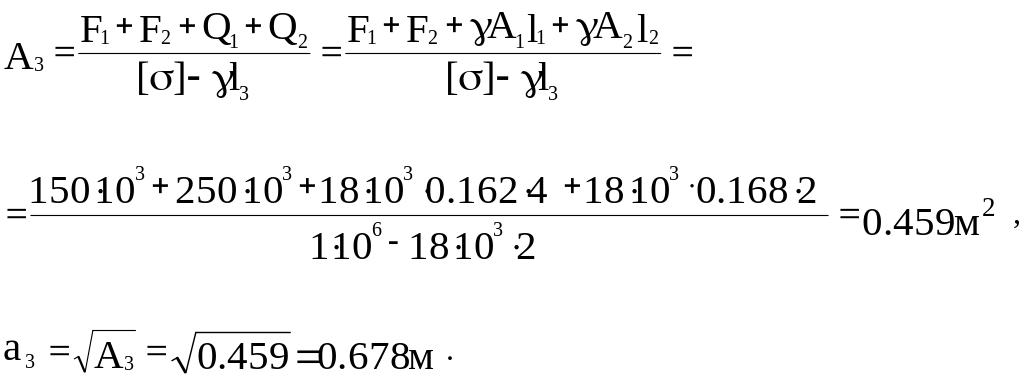
Задача №1.2. Абсолютно жорсткий брус АВ підтримується стальними стержнями 1 і 2 (рис.1.5). При а=1м, b=4м, с=2м, d=3м, D=3м, A₁=4см²=4·10^-4м², А₂=6см²=6·10^-4м², Е=2·10⁵ МПа, α=45^о, [σ]=160МПа, потрібно визначити: а) зусилля і напруження в стержнях (в частинах сили F);

б) допустиме навантаження [F].

Для визначення чотирьох невідомих – зусиль N₁, N₂, реакцій опори H_c і V_c (рис. 1.5 б) можна записати лише три рівняння статики. Таким чином, система є один раз статично невизначеною.

Через те, що в задачі необхідно визначити тільки зусилля і , з трьох рівнянь статики залишаємо тільки одне (до цього рівняння не увійдуть опорні реакції і ):

.

Щоб скласти додаткове рівняння, розглянемо деформацію заданої системи (рис. 1.5 а).

а) в)

Рис. 1.5

З подібності трикутників та

. (1.12)

Зважаючи на те, що

, .

Вираз (1.12) набуватиме вигляду

. (1.13)

У рівняннях статики, як і в статично визначених системах, усі невідомі зусилля вважаються додатними (розтягуючими )(рис. 1.5 б).Проте на деформованій схемі деякі стержні можуть бути стиснутими (стержень 1 на рис. 1.5 а). У цьому разі для приведення у відповідність знаків зусиль і деформацій вирази для деформацій стислих стержнів мають бути записані зі знаком “–“.

Для даної задачі

, .

Рівняння сумісності деформацій (1.13) набуде вигляду

. (1.14)

Підставляючи в (1.12) та (1.14) числові значення a, b, c, , , , матимемо систему рівнянь

Після розв’язання її маємо:

, .

Визначаємо напруження в стержнях

,

.

Як бачимо, найбільш напруженим (небезпечним) буде стержень 2. Записуючи для нього умову міцності

,

одержуємо

.

Задача №1.3. Для заданої стержневої системи (рис. 1.6), вважаючи горизонтальний брус абсолютно жорстким, визначити ступінь статичної невизначеності та скласти рівняння сумісності деформацій, якщо .

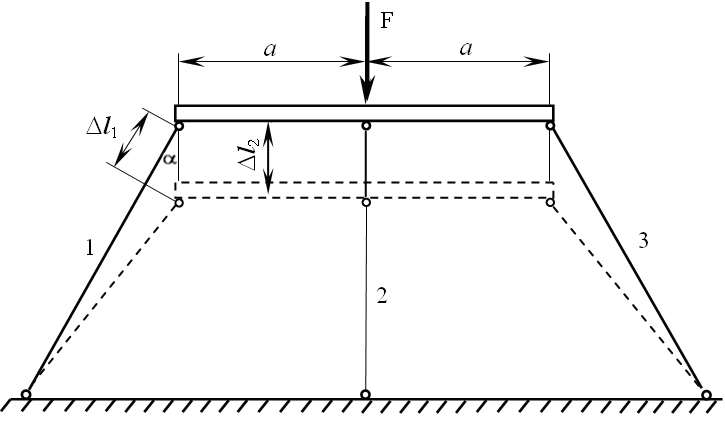
Рис. 1.6

Для визначення трьох невідомих зусиль у стержнях 1,2,3 можна скласти тільки два рівняння статики (як для системи сил, що перетинаються в одній точці). Отже, система є один раз статично невизначеною і, щоб її розрахувати, необхідно скласти одне рівняння сумісності деформацій, яке згідно з рис. 1.6 запишеться так: . Причому