5) Ортогональные векторы. Ортонормированный базис.

Определение. Два вектора называются ортогональными, если угол междуними равен прямому углу, т.е.  .

Обозначение:   – векторы   и   ортогональны.

Определение. Тройка векторов   называется ортогональной, если эти векторы попарно ортогональны друг другу, т.е.  ,  .

Определение. Тройка векторов   называется ортонормированной, если она ортогональная и длины всех векторов равны единице:  .

Замечание. Из определения следует, что ортогональная и, следовательно, ортонормированная тройка векторов является некомпланарной.

Определение. Упорядоченная некомпланарная тройка векторов  , отложенных от одной точки, называется правой (правоориентированной), если при наблюдении с конца третьего вектора   на плоскость, в которой лежат первые два вектора   и  , кратчайший поворот первого вектора   ко второму   происходит против часовой стрелки. В противном случае тройка векторов называется левой (левоориентированной).

                  

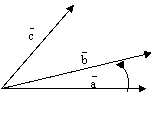
                                    рис.6.

Здесь, на рис.6 изображена правая тройка векторов  . На следующем рис.7  изображена левая тройка векторов  :

                     

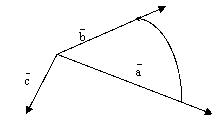
                                          рис.7.

Определение. Базис   векторного пространства   называется ортонормированным, если   ортонормированная тройка векторов.

Обозначение. В дальнейшем мы будем пользоваться правым ортонормированным базисом  , см. следующий рисунок:

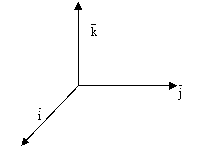
                     рис.9.

Любой вектор можно разложить по этому базису:

           .

6) Скалярное произведение

     Скалярное произведение векторов   и  : 

где   - угол между векторами   и  ; если   либо  , то 

     Из определения скалярного произведения следует, что   где, например,   есть величина проекции вектора   на направление вектора  .

     Скалярный квадрат вектора: 

     Свойства скалярного произведения:             

     Скалярное произведение в координатах 

     Если     то   

     Угол между векторами 

             Векторное произведение 

     Векторное произведение векторов   и   - вектор, обозначаемый     или   для когорого:

     1)   (  - угол между векторами   и  ,  );

     2) 

     3) тройка  ,  ,   - правая.

     Свойства векторного произведения:           если  , то   равен площади параллелограмма, построенного на приведенных к общему началу векторах   и  .

7) Векторным произведением векторов и называется вектор , который определяется следующими условиями:

1) Его модуль равен   где   - угол между векторами   и  .

2) Вектор   перпендикулярен к плоскости, определяемой перемножаемыми векторами   и  .

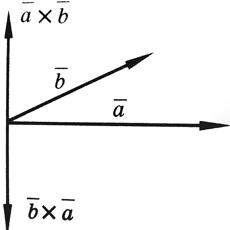
3) Вектор   направлен так, что наблюдателю, смотрящему с его конца на перемножаемые векторы   и  , кажется, что для кратчайшего совмещения первого сомножителя со вторым первый сомножитель нужно вращать против часовой стрелки (см. рисунок).

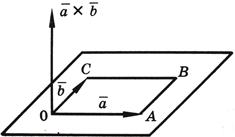
Векторное произведение векторов   и   обозначается символом  :

     (25)

или

     (26)

Основные свойства векторного произведения:

1) Векторное произведение   равно нулю, если векторы   и   коллинеарны или какой-либо из перемножаемых векторов является нулевым.

2) При перестановке местами векторов сомножителей векторное произведение меняет знак на противоположный (см. рисунок):

Векторное произведение не обладает свойством переместительности.