2) Операция сложения двух векторов - правило треугольника.

3)Линейная комбинация векторов

     Линейной комбинацией векторов   называют вектор

     

где   - коэффициенты линейной комбинации. Если   комбинация называется тривиальной, если   - нетривиальной.

     Линейная зависимость и независимость векторов 

     Система   линейно зависима     что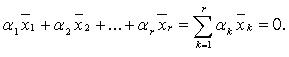 

     Система   линейно независима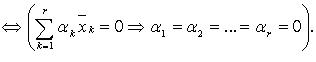 

     Критерий линейной зависимости векторов 

     Для того чтобы векторы   (r > 1) были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов являлся линейной комбинацией остальных.

3) Базис. Разложение векторов по базису.

     Определение. Базисом в пространстве Rⁿ называется любая система из n-линейно независимых векторов. Каждый вектор из Rⁿ, не входящих в базис, можно представить в виде линейной комбинации базисных векторов, т.е. разложить по базису.      Пусть   – базис пространства Rⁿ и  . Тогда найдутся такие числа λ₁, λ₂, …, λ_n, что  .      Коэффициенты разложения λ₁, λ₂, …, λ_n, называются координатами вектора   в базисе В. Если задан базис, то коэффициенты вектора определяются однозначно.      Пример. Доказать, что векторы   образуют базис в R³.      Решение. Покажем, что равенство   возможно только при λ₁ = λ₂ = λ₃ =0:            или 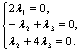      Решив систему, получим λ₁=0, λ₂=0, λ₃=0. Так как все λ_i=0 (i=1,2,3), то   - линейно независимы. Они могут составить базис в R³.      Очевидно, любой новый набор из векторов       может тоже быть взятым в качестве базиса в R³. Итак, базис может быть выбран неединственным образом.     Замечание. В каждом n-мерном векторном пространстве можно выбрать бесчисленное множество различных базисов. В различных базисах один и тот же вектор имеет различные координаты, но единственные в выбранном базисе.

4) Проекция вектора на ось. Координаты вектора и его свойства

Пусть в декартовых координатах OXYZ вектор AB задан координатами начала А(х₁;у₁;z₁) и конца В(х₂;у₂;z₂) этого вектора.

Нам уже известно определение проекции точки на ось как основания перпендикуляра, проходящего через заданную точку.

Проекцией вектора AB на ось ОХ называется разность между абсциссами проекции конца и начала вектора AB.

т.е. ПР_ох AB=х₂-х₁, ПР_оу AB=у₂-у₁, ПР_oz AB=z₂-z₁.

Для краткости используют следующие обозначения данных проекций:

ПР_ох AB=Х, ПР_оу AB=У и ПР_оz AB=Z, тогда получаем Z=z₂-z_1, Х=х₂-х₁,

У=у₂-у₁.

Из рассмотренных формул следует, что проекция вектора на любую ось есть длина отрезка между основаниями перпендикуляров, опущенных из точек А и В на эту же ось, взятая со знаком “+”, если направление отрезка и направление оси совпадают, и со знаком “-“, если они противоположны.

Можно доказать, что: а) если проекции вектора заданы, то они однозначно определяют сам вектор; б) если два вектора равны, то они имеют равные проекции,

поэтому проекции вектора на оси называют его координатами

AB=(Х;У;Z).

Некоторые свойства проекции вектора на ось: 

Для определённости будем рассматривать эти свойства относительно оси ОХ.

Предположим, что вектор a=AB образует с осью ОХ угол φ.

Угол между вектором a и осью определим следующим образом.

Через произвольную точку пространства проведем 2 луча – один ║ положительному направлению ОХ, а другой - ║ направлению вектора. Угол между лучами определяет угол между вектором и осью.

Проекция вектора на ось ОХ равна произведению длины вектора на косинус угла между вектором и осью.

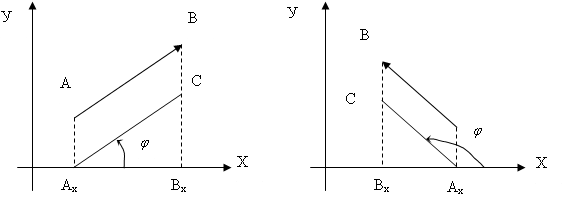
Рис. 1.15. Проекция вектора на ось

Пусть задан вектор AB и А_хВ_х - его проекция на ось ОХ. Опустив перпендикуляр из точки А на ось ОХ, получаем А_х.

Проведем через точку А прямую ║ вектору AB до пересечения ВВ_х  и получим точку с. Из треугольника СВ_хА имеем

ПР _ох AB=А _хВх=│А _хC│cosφ=│АВ│cosφ

Проекция суммы нескольких векторов на ось равна сумме проекций складываемых векторов на ту же осью;

При умножении вектора AB на число m, его проекция умножится на то же число m.