4) Транспонирование матриц

Транспонирование матриц – переход от матрицы  А  к матрице, в которой строки и столбцы поменялись местами с сохранением порядка.

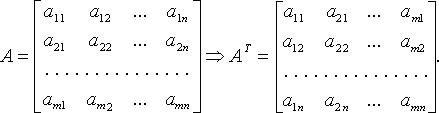
     Свойства:       

5) Обратная матрица

Рассмотрим квадратную матрицу

  .

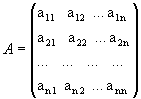Обозначим Δ =det A.

Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, илиособенной, если Δ = 0.

Квадратная матрица В есть обратная матрица для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В.

Теорема. Для того, чтобы матрица А имела обратную матрицу, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

Обратная матрица матрице А, обозначается через А^1, так что В = А^1 и вычисляется по формуле

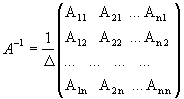,                                               (1)

где А _{i j} - алгебраические дополнения элементов a _{i j} матрицы A..

Вычисление A^-1 по формуле (1) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить A^-1 с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ранга матрицы можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.

6) Матричный метод решения систем линейных уравнений.

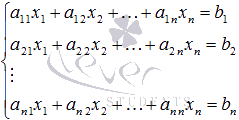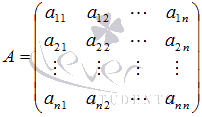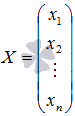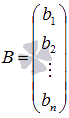вида  , которые в матричной форме записываются как  , где   - основная матрица системы,   - матрица-столбец неизвестных переменных,   - матрица свободных членов. Сначала опишем суть матричного метода, остановимся на условии применимости этого метода, далее подробно разберем решения нескольких примеров. Сразу оговоримся, что решение систем линейных алгебраических уравнений матричным методом и решение СЛАУ с помощью обратной матрицы есть одно и то же. Поэтому рекомендуем освежить в памяти теорию раздела обратная матрица: определение, свойства, методы нахождения. Приступим. Пусть для матрицы А порядка n на n существует обратная матрица  . Умножим обе части матричного уравнения   слева на   (порядки матриц A ⋅ X и В позволяют произвести такую операцию, смотрите статью операции над матрицами, свойства операций). Имеем  . Так как для операции умножения матриц подходящих порядков характерно свойство ассоциативности, то последнее равенство можно переписать как  , а по определению обратной матрицы   (E– единичная матрица порядка n на n), поэтому 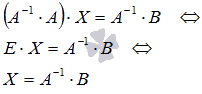  Таким образом, решение системы линейных алгебраических уравнений по матричному методу определяется равенством  . Другими словами, решение СЛАУ находится с помощью обратной матрицы  . Мы знаем, что квадратная матрица А порядка n на n имеет обратную матрицу   только тогда, когда ее определитель не равен нулю. Следовательно, СИСТЕМУ n ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С nНЕИЗВЕСТНЫМИ МОЖНО РЕШАТЬ МАТРИЧНЫМ МЕТОДОМ ТОЛЬКО ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ ОСНОВНОЙ МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ НУЛЯ. Рассмотрим матричный метод на примерах. В некоторых примерах мы не будем подробно описывать процесс вычисления определителей матриц, при необходимости обращайтесь к статье вычисление определителя матрицы.