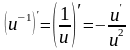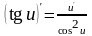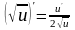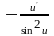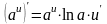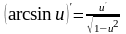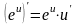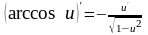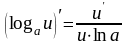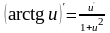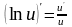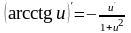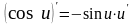- •Введение
- •1. Определение производной. Дифференцирование функций
- •16. (Логарифмическая производная).
- •2. Геометрические приложения производной. Уравнения касательной и нормали
- •3. Дифференцирование неявных функций
- •4. Дифференциал функции. Применение дифференциала к приближенным вычислениям
- •5. Производные и дифференциалы высших порядков
- •6. Правило Лопиталя
- •7. Применение производной к исследованию функций и построению графиков
- •8. Нахождения наибольшего и наименьшего значений непрерывной функции на отрезке
- •9. Задачи на отыскание наибольших и наименьших значений величин
- •Варианты заданий для ргр
- •Литература
- •Формат Объем Тираж Заказ
Министерство образования и науки Российской Федерации
Государственное образовательное учреждение
высшего профессионального образования
«Брянская государственная инженерно-технологическая академия»
Кафедра математики
“Приложения производной функции одной действительной переменной”
Методические указания и задания к расчетно-графической работе для студентов всех направлений подготовки бакалавров очной формы обучения
Брянск 2011
Министерство образования и науки Российской Федерации
Государственное образовательное учреждение
высшего профессионального образования
«Брянская государственная инженерно-технологическая академия»
Кафедра математики
УТВЕРЖДЕНЫ
научно-методическим
советом академии
Протокол № ____
oт “____”___________2011 г.
“ Приложения производной функции одной действительной переменной ”
Методические указания и задания к расчетно-графической работе для студентов всех направлений подготовки бакалавров очной формы обучения
Брянск 2011
Авторы:
Антоненкова Ольга Евгеньевна
Баранова Ирина Михайловна
Часова Наталья Александровна
Рецензент: профессор каф. физики, к. физ.-мат. наук Евтюхов К. Н.
Рассмотрены УМК МТФ
Протокол № от
Содержание
Введение 5
1. Определение производной. Дифференцирование функций 6
2. Геометрические приложения производной. Уравнения касательной и нормали 7
3. Дифференцирование неявных функций 10
4. Дифференциал функции. Применение дифференциала к приближенным вычислениям 12
5. Производные и дифференциалы высших порядков 14
6. Правило Лопиталя 15
7. Применение производной к исследованию функций и построению графиков 18
8. Нахождения наибольшего и наименьшего значений непрерывной функции на отрезке 30
9. Задачи на отыскание наибольших и наименьших значений величин 31
Варианты заданий для РГР 35
Литература 47
Введение
Дифференциальное исчисление было создано Ньютоном и Лейбницем в конце 17 столетия на основе двух задач:
1) о разыскании касательной к произвольной линии
2) о разыскании скорости при произвольном законе движения
Еще раньше понятие производной встречалось в работах итальянского математика Тартальи (около 1500 – 1557 гг.) – здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда.
В 17 веке на основе учения Г.Галилея о движении активно развивалась кинематическая концепция производной. Различные изложения стали встречаться в работах у Декарта, французского математика Роберваля, английского ученого Л. Грегори. Большой вклад в изучение дифференциального исчисления внесли Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс.
1. Определение производной. Дифференцирование функций
Производной функции у = f (x) называется предел отношения приращения функции к соответствующему приращению аргумента, когда приращение аргумента стремиться к нулю:
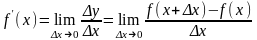 .
(1)
.
(1)
Если
этот предел конечный, то производная
существует, а функция f
(x) называется
дифференцируемой в точке x.
Производная обозначается или
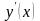 ,
или
,
или
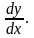 Процесс нахождения производной называется
дифференцированием функции.
Процесс нахождения производной называется
дифференцированием функции.
Правила дифференцирования функций. Пусть С R – постоянная, и = и (х), v = v(x) — функции, имеющие производные.
1. |
С ' =0. |
4. |
(Си)' =С ∙ u' . |
2. |
(u ± v)' = и' ± v'. |
5. |
|
3. |
(u ∙ v)’ =u’ ∙ v + u ∙ v’. |
|
|
6. Правило дифференцирования сложной функции. Если функция y = f (u) дифференцируема по и, а функция и = φ (x) – по х, то сложная функция y = f (φ (x)) имеет производную y' =f ' (u) ∙ u' (x) .
Таблица производных элементарных функций
1. |
|
9. |
|
2. |
|
10. |
|
3. |
|
11. |
(ctg
u) |
4. |
|
12. |
|
5. |
|
13. |
|
6. |
|
14. |
|
7. |
|
15. |
|
8. |
|
|
|
16. (Логарифмическая производная).
2. Геометрические приложения производной. Уравнения касательной и нормали
Геометрический смысл производной состоит в следующем: производная функции f(x) в точке х0 равна угловому коэффициенту касательной к кривой y=f(x) в точке (х0; f(x0)), т.е. равна тангенсу угла наклона касательной к положительному направлению оси Ох (рис.1).
Если
функция f
дифференцируема в точке х0,
то график этой функции имеет касательную,
угловой коэффициент которой равен
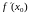 .
.

Рисунок 1 – Геометрическое приложение производной.
Тогда уравнение касательной имеет вид
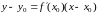 .
(2)
.
(2)
Прямая,
проходящая через точку M0(x0;y0)
и перпендикулярная к касательной,
называется нормалью
к графику функции
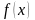 в точке M0(x0;y0).
Тогда
в точке M0(x0;y0).
Тогда
 ,
и, значит, уравнение
нормали
имеет вид
,
и, значит, уравнение
нормали
имеет вид
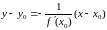 .
(3)
.
(3)
Углом между двумя кривыми в точке их пересечения называется угол между касательными к кривым в этой точке.
Угол
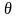 между двумя прямыми с угловыми
коэффициентами
между двумя прямыми с угловыми
коэффициентами
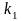 и
и
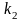 находится по формуле:
находится по формуле:
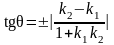 ,
(4)
,
(4)
причем знак “плюс” соответствует острому углу , а знак “минус”– тупому.
Если
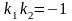 ,
то касательные – взаимно
перпендикулярны,
а кривые называются ортогональными.
,
то касательные – взаимно
перпендикулярны,
а кривые называются ортогональными.
Пример
2.1. Составить
уравнения касательной и нормали к
графику функции
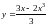 в точке с абсциссой x0=1.
в точке с абсциссой x0=1.
Решение. Уравнение касательной к графику функции y=f(x) в точке с абсциссой x0 имеет вид (2).
Вычислим
значение функции в данной точке:
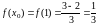 .
.
Найдем производную функции и ее значение в данной точке:
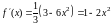 ,
,
 .
.
Подставим найденные значения в уравнение касательной:
 ,
, 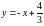 – уравнение касательной.
– уравнение касательной.
Уравнение нормали к графику функции y=f(x) в точке с абсциссой x0 имеет вид (3).
Подставим найденные значения в это уравнение:
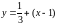 ,
, 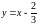 – уравнение нормали.
– уравнение нормали.
Пример
2.2.
Найти
уравнение касательной к графику функции
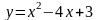 ,
которая параллельна прямой
,
которая параллельна прямой
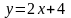 .
Сделать чертеж.
.
Сделать чертеж.
Решение.
График функции
– парабола. Так как
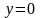 при
при
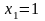 ,
,
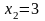 ,
то вершиной параболы является точка
(2; –1). По условию, касательная
,
то вершиной параболы является точка
(2; –1). По условию, касательная
 к параболе и данная прямая
к параболе и данная прямая
 с уравнением
параллельны; значит их угловые коэффициенты
равны: k1
= y′1
с уравнением
параллельны; значит их угловые коэффициенты
равны: k1
= y′1
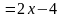 ,
,
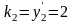 ,
,
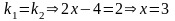 .
Следовательно, x0
= 3 – абсцисса точки касания
.
Следовательно, x0
= 3 – абсцисса точки касания
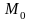 параболы и прямой
,
параболы и прямой
,
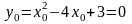 – ее ордината. Таким образом, уравнение
касательной
имеет вид:
– ее ордината. Таким образом, уравнение
касательной
имеет вид:
 (рис. 2).
(рис. 2).
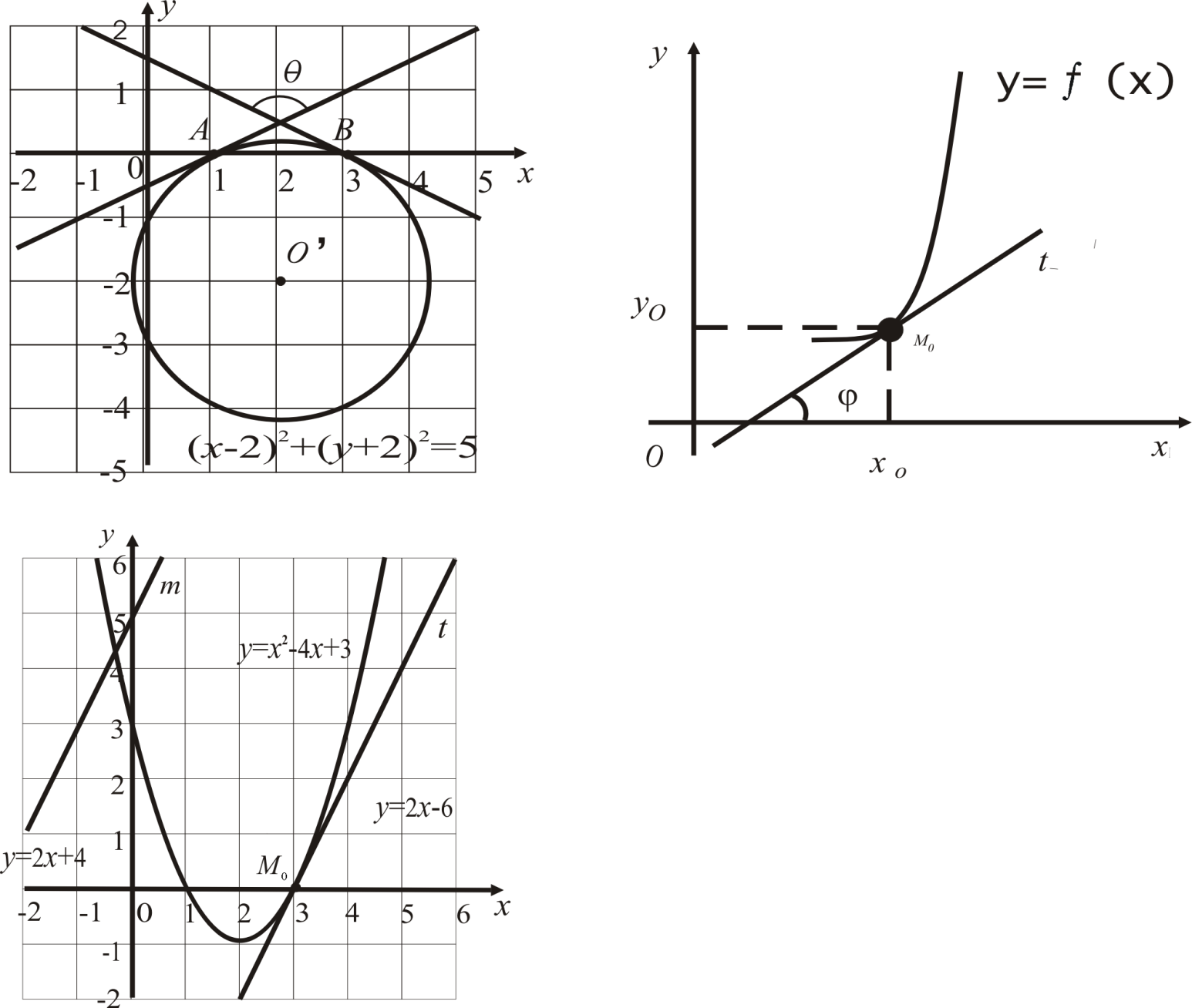
Рисунок 2 – Иллюстрация к примеру 2.2.

 .
.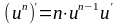
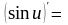 cos
u
u
cos
u
u