5. Импеданс и фазовые соотношения между смещением и

вынуждающей силой

Для удобства анализа фазовых соотношений при вынужденных колебаниях выпишем результаты решения уравнения . Во-первых, закон гармонической вынуждающей силы мы записали в форме закона косинуса:

F_x(t) = F₀ cost. (12)

Решением дифференциального уравнения, отвечающего установившейся части вынужденных колебаний, является функция

x(t) = Хsin (t  ) = Хcos (t   ) = Хcos (t  ), (13)

где  =  + . Напомним, угол  обусловлен (см. рис.14) наличием реактивного сопротивления в импедансе .

Из сравнения (12) и (13) следует:

между смещением x(t) = Хcos (t  ) и вынуждающей силой F_x(t) = F₀ cost существует полный сдвиг фаз  =  + . Напомним, фаза  обусловлена наличием в колебательной системе реактивной составляющей импеданса ( ). При  = 0, т.е. при равенстве составляющих реактивного сопротивления ( ), смещение отстает от силы на радиан (на 90⁰). Так как собственная частота осциллятора , то при частота вынуждающей силы равна собственной частоте: = .

Дополнительный сдвиг выражен в уравнении (9) множителем (i).

При понижении частоты вынуждающей силы (при   0) фаза  стремится к значению  (см. рис. 14-б). Следовательно, при   0 полная фаза  стремится к нулю:  = ( + )  0. Таким образом, при   0 начинает исчезать сдвиг фаз между смещением x(t) и силой F_x(t).

П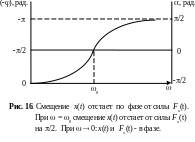 ри высоких частотах ( ) фаза   (см. рис. 14-а). Следовательно, в этом случае полная фаза  = ( + )  . Итак, при    отставание смещения по фазе от вынуждающей силы стремится к значению  радиан (180⁰).

На рисунке 16 приведен график полной разности фаз ( ) =  ( + ) между смещением x(t) = Хcos (t  ) и вынуждающей силой F_x(t) = F₀ cost в зависимости от частоты  вынуждающей силы. На этом же графике показано соотношение между полной фазой ( ) и фазой .

2.6. Смещение как сумма двух его компонент. Резонанс смещения и его анализ

Амплитуда смещения (11) зависит от частоты  вынуждающей силы X = X (). При некоторой частоте, называемой резонансной частотой _р, амплитуда смещения будет максимальной – наблюдается резонанс смещения. Резонансная частота _р. находится стандартно: необходимо приравнять нулю первую производную (11) по частоте  (достаточно взять производную от подкоренного выражения). Получим:

_р. = .

Если частота вынуждающей силы равна резонансной частоте  = _р., то амплитуда смещения осциллятора (11) будет определяться выражением:

X_р. = = = ,

где ^/ = - частота затухающих колебаний осциллятора.

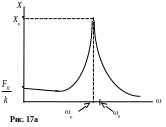
На рис. 17-а приведен график зависимости амплитуды смещения от частоты вынуждающей силы X = X (), т.е. график уравнения (11). Этот график называют резонансной кривой смещения или амплитудно-частотной характеристикой (АЧХ) смещения колебательной системы.

Проведем анализ резонансной кривой (11). Вначале раскроем синус в уравнении смещение (12*) и учтем, что Х = :

x(t) = Хsin(t  ) = sin(t  ) = sint cos  cost sin.

Из рисунка 14 видно, что cos = и sin = , где  - активная составляющая импеданса, (mk/) - реактивная составляющая импеданса. Имеем:

x(t) = sint  cost.

Составляющая смещения ( cost) находится в противофазе (стоит знак минус!) с силой F_x(t) = F₀ cost. Назовем эту составляющую смещения – реактивной составляющей. Активная составляющая ( sint) отстает по фазе от силы на радиан (на 90⁰). Относительный сдвиг фаз между компонентами составляет радиан (90⁰). Сумма векторных диаграмм компонент смещения (относительный сдвига фаз между компонентами 90⁰!) равна, разумеется, результирующей амплитуде (11):

Х = .

Принимая во внимание, что и  = , представим выражения для амплитуд компонентов смещения – реактивной X_реакт. и активной X_акт. – как функции частоты  в виде:

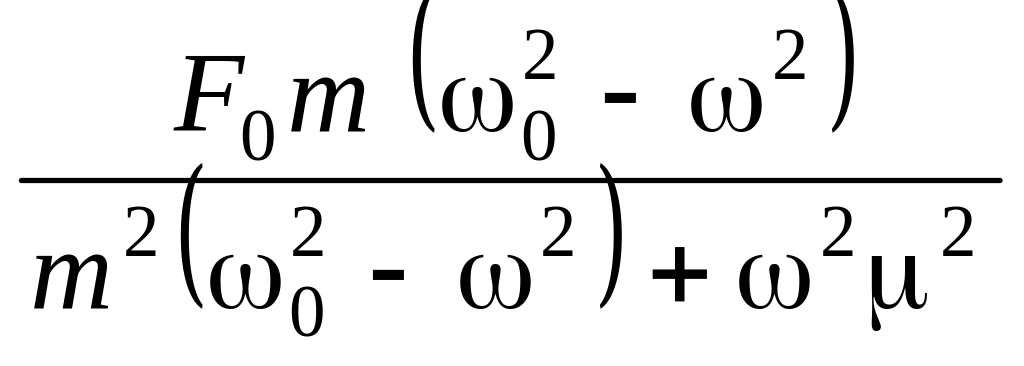X_реакт. =  = (*); X_акт. = = . (**)

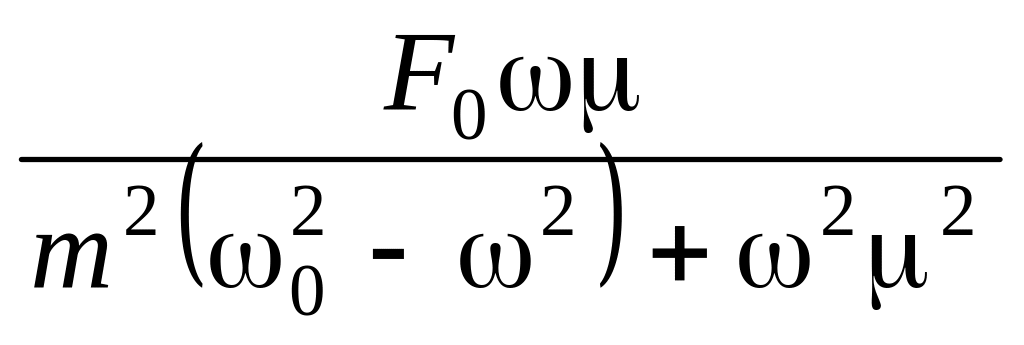Из формулы (**) следует, что максимальное значение активной составляющей смещения происходит при  = ₀.

На рисунке 17-б приведены графики реактивной составляющей амплитуды смещения (*) – кривая (3), активной составляющей (**) – кривая (2) и результирующей амплитуды (формула 11) – кривая (1).

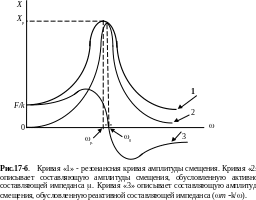
Из (*) и (**) видно, что при  = ₀ кривая (3) приходит через нуль, а кривая (2) – через максимум. При сложении кривых резонансная амплитуда X_р резонансная частота несколько смещается в сторону низких частот: _р < ₀. Выше мы получили, что

_р. = .

В § 2.10 покажем, что при  = ₀ наблюдается максимальное поглощение энергии, поступающей от вынуждающего источника энергии, и это поглощение энергии связано с активной составляющей импеданса . Кривая зависимости поглощения энергии от частоты похожа на кривую зависимости амплитуды смещения от частоты, отображенная кривой (2) на рисунке 17-б. Кривая (3) связана с накоплением энергии в осцилляторе и связана с реактивной составляющей импеданса . Оказывается, что именно реактивная составляющая определяет скорость распространения волн в среде.