
- •Методические указания к лабораторным работам по курсу "Сопротивление материалов", часть II
- •Предметный указатель
- •Эксперимент.
- •Лабораторная работа № 6
- •Теория.
- •Эксперимент
- •Определение изогнутой оси стержня
- •Т аблица 2
- •Лабораторная работа № 7
- •Теория.
- •II. Эксперимент
- •Обработка экспериментальных результатов
- •Лабораторная работа № 8
- •Теория.
- •II. Эксперимент
- •Лабораторная работа № 9
- •Теория.
- •II. Эксперимент
- •О бразец и схема испытания
- •Лабораторная работа № 10
- •Теория.
- •II. Эксперимент
- •Литература
- •Писаренко г.С. И др. Сопротивление материалов. –Киев: "Вища школа",1974, 672 с.
- •Сидорин и.И. И др. Основы материаловедения. –м.: Машиностроение, 1976, 436 с.
II. Эксперимент
Машина для испытаний (указать тип машины).
Измеритель стрелы прогиба.
Л
 инейка.
инейка.
Т аблица
наблюдений
аблица
наблюдений
 Эксперимент
заключается в установлении зависимостей
"нагрузка – перемещение" для
системы и затем для её элементов при
упругом деформировании.
Эксперимент
заключается в установлении зависимостей
"нагрузка – перемещение" для
системы и затем для её элементов при
упругом деформировании.
Обработка экспериментальных результатов
По результатам наблюдений построить графики "нагрузка – перемещения" с равномерной оцифровкой осей и в одном масштабе по оси перемещений. Указать все экспериментальные точки и провести усредняющие прямые линии. Если усреднённая линия (прерывистая на иллюстрации представления графиков) не проходит через начало координат, провести соответствующую линию параллельную усредненной. В работе использовать линии, проходящие через начало координат.
С равнение
теоретического и экспериментального
решений
равнение
теоретического и экспериментального
решений
Указать
нагрузку на систему Р
(назначить
произвольно) и по графикам определить
значения
![]() и
и
![]() .
.
Определить
![]() и
и
![]() для принятого значения нагрузки Р
по результатам теоретического решения
(см. теория).
для принятого значения нагрузки Р
по результатам теоретического решения
(см. теория).
Установить погрешности:
![]() ,
,
![]() ,
,
Сравнить соотношения:
![]() ,
, ![]() .
.
Примечание:
Модули упругости материала балок
![]() и
и
![]() можно определить по соответствующим
графикам (см. "Испытание на изгиб").
можно определить по соответствующим
графикам (см. "Испытание на изгиб").
Выводы. Заключение о результатах проверки с анализом возможных источников погрешностей в эксперименте.
Лабораторная работа № 8
ИССЛЕДОВАНИЕ КОСОГО ИЗГИБА
Цель:
экспериментальная проверка основных
положений теории косого изгиба:
определение положения нейтральной
линии
![]() и перемещений
и перемещений
![]() .
.
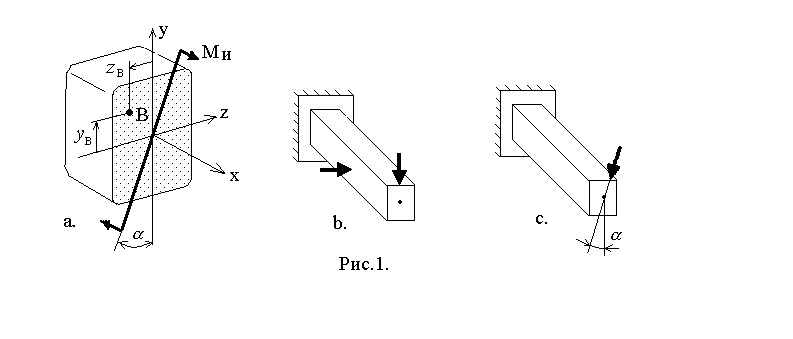
Теория.
Под
косым изгибом понимается такой вид
изгиба, когда плоскость действия
изгибающего момента
![]() не совпадает с главными центральными
осями поперечного сечения стержня y,
z
(рис.1,а).
не совпадает с главными центральными
осями поперечного сечения стержня y,
z
(рис.1,а).
Косой изгиб возникает, например, если перпендикулярная к оси стержня нагрузка действует в разных плоскостях (рис.1b), или ориентирована произвольно по отношению к главным центральным осям (рис.1,с).
Н а
плоскости можно использовать следующее
изображение моментов перпендикулярных
к ней (рис.2). Косой
изгиб представляется, как совокупность
двух плоских изгибов в главных плоскостях
моментами
а
плоскости можно использовать следующее
изображение моментов перпендикулярных
к ней (рис.2). Косой
изгиб представляется, как совокупность
двух плоских изгибов в главных плоскостях
моментами
![]() и
и
![]() .
Результирующий момент определяется
геометрической суммой:
.
Результирующий момент определяется
геометрической суммой:
![]() ,
,
а угол наклона, если его отсчитывать от оси у, отношением:
![]() .
.
 Оси
следует направлять таким образом, чтобы
результирующий момент проходил через
I
и III
квадранты.
Оси
следует направлять таким образом, чтобы
результирующий момент проходил через
I
и III
квадранты.
Нормальные напряжения в любой точке сечения определяются алгебраической суммой напряжений от двух моментов:
![]() .
.
Координаты
точки имеют знаки. Так, на рис.1,а координата
![]() отрицательна,
отрицательна,
![]() положительна. Следовательно, во всех
точках I
квадранта напряжения положительны, а
в точках III
квадранта отрицательны. Нейтральная
линия проходит через II
и IV
квадранты, и координаты её точек
положительна. Следовательно, во всех
точках I
квадранта напряжения положительны, а
в точках III
квадранта отрицательны. Нейтральная
линия проходит через II
и IV
квадранты, и координаты её точек
![]() находятся из условия отсутствия
напряжений в них:
находятся из условия отсутствия
напряжений в них:
![]() .
.
Нейтральная линия проходит через центр тяжести сечения, и её положение можно определить углом наклона к оси z:
![]() .
.
Если
![]() ,
то нейтральная линия в сечении стержня
не перпендикулярна плоскости действия
результирующего изгибающего момента
(
,
то нейтральная линия в сечении стержня
не перпендикулярна плоскости действия
результирующего изгибающего момента
(![]() ),
стержень "предпочитает" изгибаться
не в его плоскости, как это бывает при
плоском изгибе. Именно этим и обусловлено
название "косой" изгиб. Для сечений
с равными моментами инерции
),
стержень "предпочитает" изгибаться
не в его плоскости, как это бывает при
плоском изгибе. Именно этим и обусловлено
название "косой" изгиб. Для сечений
с равными моментами инерции
![]() нейтральная линия перпендикулярна
плоскости действия результирующего
момента и "косого" изгиба нет.
нейтральная линия перпендикулярна
плоскости действия результирующего
момента и "косого" изгиба нет.
Линейные перемещения сечений определяются геометрической суммой перемещений по направлениям главных осей.
