Содержание задания

Задача 1. Построить две проекции заданных поверхностей и проекции линии сечения поверхностей проецирующей плоскостью α. Определить видимость линии сечения. Проставить размеры.

Задача 2. Построить натуральную величину сечения, применив для этого любой способ преобразования проекций.

Объем работы

Эпюр1301 выполняется на листе ватмана формата А3 (297х420мм), расположенном вертикально, в масштабе 1:1, в карандаше, с соблюдением требований стандартов на оформление чертежей, основная надпись по форме 1 (см. рис. 2).

Последовательность выполнения эпюра 1301

Пример выполнения и оформления эпюра 1301 приведен на рис. 2.1.

Задача 1. Для построения проекций линии пересечения заданных поверхностей с фронтально проецирующей плоскостью α определены проекции точек пересечения параллелей усеченного конуса вращения и граней призмы с плоскостью α.

Линия пересечения конуса плоскостью построена по точкам 2 – 6:

точка 2 принадлежит основанию конуса;

точка 4 – передней образующей конуса;

точка 6 – крайней правой образующей конуса;

точки 2 и 6 являются одновременно низшей и высшей точками линии пересечения.

Горизонтальные проекции 2₁,3₁,4₁ найдены с помощью соответствующих параллелей конуса.

Плоскость α пересекает горизонтально проецирующую призму (основание призмы – квадрат со стороной 100 мм, высота призмы – 25 мм) по прямоугольнику 1-2-2-1, а горизонтально проецирующее призматическое отверстие – по прямоугольнику 3- 4- 5- 5- 4- 3.

Задача 2. Натуральная величина сечения определена способом перемены плоскостей проекций.

Плоскость проекций, на которой построена натуральная величина сечения, параллельна фронтально проецирующей плоскости α, осевая линия сечения 0 – 6 параллельна фронтальному следу α_П2 плоскости α, 0-6  α_П2. При нанесении штриховки условно заменяется поверхность технической формы твердотельной моделью.

Рис. 2.1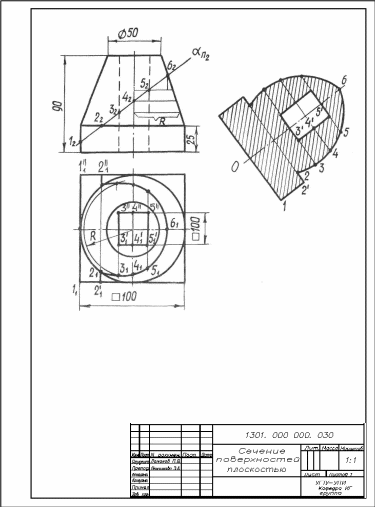

3. Эпюр 1401 «Взаимное пересечение поверхностей.

Развертка»

Методические указания

Цель задания – закрепление знаний по решению позиционных задач на построение проекций линии пересечения поверхностей. Построение разверток поверхностей с нанесением линии пересечения поверхностей.

Содержание задания

Задача 1. Построить три проекции заданных поверхностей и проекции линий их взаимного пересечения, используя в качестве посредников вспомогательные секущие плоскости. Обозначить вспомогательные секущие плоскости. Проставить размеры.

Задача 2. Построить одну (фронтальную) проекцию заданных пересекающихся поверхностей вращения и линию их взаимного пересечения, используя в качестве посредников вспомогательные концентрические сферы. Проставить размеры.

Задача 3. Построить развертку поверхности, обозначенной буквой Р в индивидуальном задании.

Объем работы

Эпюр1401 выполняется на листе ватмана формата А2 (420х594мм) в масштабе 1:1, в карандаше, с соблюдением требований стандартов на оформление чертежей, основная надпись по форме 1 (см. рис. 2).

Последовательность выполнения эпюра 1401

Пример выполнения и оформления эпюра 1401 приведен на рис. 3.1.

Задача 1. Геометрическая фигура составлена из трех поверхностей: усеченного конуса, профильно проецирующей четырехгранной призмы и половины фронтально проецирующего цилиндра.

Для построения линий пересечения поверхностей определяются точки, общие для этих поверхностей, для чего используются вспомогательные секущие плоскости.

Пересечение половины цилиндра и усеченного конуса

Линия пересечения усеченного конуса и полуцилиндра – пространственная кривая.

Образующие цилиндра перпендикулярны фронтальной плоскости проекций П₂, поэтому проекции линии пересечения поверхности на П₂ определяются без дополнительных построений. Фронтальные проекции точек 1, 2 и 3 линии пересечения расположены на окружности основания цилиндра. Точка 1 принадлежит передней образующей конуса и верхней образующей цилиндра, точка 3 – крайней левой образующей конуса.

Для построения горизонтальной и профильной проекций линии пересечения проведены вспомогательные горизонтальные плоскости уровня 1, 2, 3, перпендикулярные оси усеченного конуса. Вспомогательные секущие плоскости пересекают конус по окружностям, а цилиндр – по прямоугольникам. На пересечении горизонтальных проекций, соответствующих каждой секущей плоскости окружностей и прямоугольников, находятся точки, принадлежащие линии пересечения полуцилиндра и конуса 1₁, 2₁, 3₁ и т.д. Профильная проекция линии пересечения построена по точкам 1₃, 2₃, 3₃ .

Пересечение четырехгранной призмы и усеченного конуса

Линия пересечения призмы и конуса – кривая, состоящая из отрезков плоских кривых линий (частей эллипсов). Все точки пересечения принадлежат как поверхности конуса, так и поверхности призмы. Проекция линии пересечения на плоскость П₃ совпадает с проекцией самой призмы (квадрат со стороной 36 мм), так как призма – проецирующая поверхность, ее грани перпендикулярны плоскости П₃.

Для построения горизонтальной проекции линии пересечения поверхностей выбираются горизонтальные вспомогательные секущие плоскости (₁…,_n), каждая из которых пересекает обе рассматриваемые поверхности. В сечении конуса плоскостью ₁ будет окружность, радиус которой определяется расстоянием от оси конуса до очерковой образующей, измеряемым по следу секущей плоскости.

В сечении призмы этой же плоскостью получается прямоугольник, ширина которого определяется точками пересечения секущей плоскости ₁ с гранями призмы.

Построение горизонтальных проекций окружности и прямоугольника определяет точки их пересечения, которые являются искомыми, т.е. точками, принадлежащими линии пересечения усеченного конуса и призмы.

Плоскости  проводятся через характерные точки: на ребрах призмы (4, 6, 8) и промежуточные (6, 7).

Точки 4 и 8 являются высшей и низшей точками линии пересечения и одновременно принадлежат крайней левой образующей конуса и ребрам призмы. Точка 6 определяет видимость линии пересечения на горизонтальной плоскости проекций.

По двум проекциям линии пересечения (горизонтальной и профильной) строится третья (фронтальная).

При определении видимости проекций линии пересечения заданные поверхности рассматриваются как непрозрачные оболочки.

Задача 2. Геометрическая фигура составлена из усеченного конуса и произвольной поверхности вращения. Линия пересечения поверхностей вращения – биквадратная пространственная кривая.

Оси поверхностей вращения пересекаются. Представленные поверхности имеют общую плоскость симметрии, параллельную фронтальной плоскости проекций П₂. Исходя из перечисленных условий задачу по построению линии пересечения поверхностей можно решать в одной проекции на плоскости П₂ способом вспомогательных секущих плоскостей, проводимых из точки пересечения осей О₂.

Точки пересечения очерков заданных поверхностей (1₂ и 6₂) являются верхней и нижней точками линии пересечения.

Минимальный радиус сферы (R_min) равен большему нормальному радиусу, проведенному из точки пересечения осей вращения к образующей каждой из поверхностей.

Сфера пересекает каждую из поверхностей по окружности, плоскость которой перпендикулярна оси вращения поверхности и поэтому проецируется на плоскость П₂ в виде прямой линии. Строится точка пересечения проекций окружностей (точка 5₂).

Произвольно проводятся сферы радиусами между R_min и R_max – расстояние от точки О₂ до 1₂. Построив точки 2₂, 3₂ и 4₂ и соединив их плавной линией с точками 1₂, 6₂, определяют фронтальную проекцию линии пересечения заданных поверхностей.

Задача 3. Для построения развертки поверхности часть конуса, ограниченную линией пересечения и верхним основанием вычерчивают отдельно на свободном поле чертежа. Достраивают вершину конуса S (рис. 3.1). Развертка поверхности усеченного конуса строится способом аппроксимации.

Аппроксимируем поверхность конуса вписанной в него двенадцатигранной пирамидой. Для этого в круговое основание конуса (на приведенном примере показана половина основания конуса – полуокружность) вписывается правильный двенадцатиугольник. Через вершины многоугольника проводим ребра пирамиды.

Развертка прямого кругового конуса – часть кругового сектора, радиус которого равен величине очерковой образующей конуса S или S. Очерковые образующие S и S проецируются в натуральную величину на фронтальную плоскость проекций, так как являются фронтальными прямыми. Длина дуги сектора равна периметру двенадцатиугольника, вписанного в круговое основание ₁₁-₁₁,…,₁₁ -₁₁.

Натуральную величину образующих конуса SA, SB, SC, SD, SE определяем способом вращения вокруг оси ОS, перпендикулярной горизонтальной плоскости проекций. Построенные точки 1, А, В, С, и т. д. соединяются плавной кривой линией.