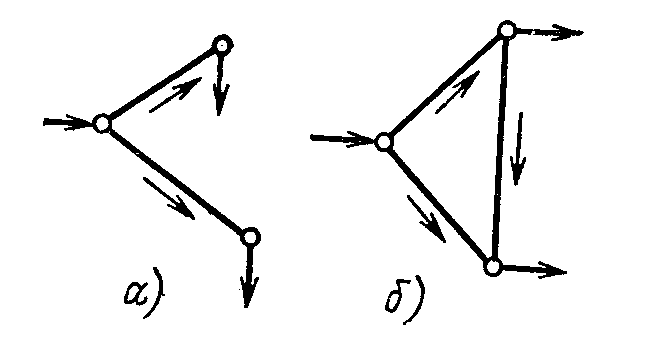
Схема, содержащая хотя бы один контур, называется замкнутой. В замкнутой сети есть хотя бы один узел, по­- лучающий питание по двум или более ветвям (рис. 3.1,б). Отключение какой-либо ветви не приводит к прекращению питания.

Элементы электрических схем делятся на активные и пассивные.

П

Рис. 3.1. Схема соединения электрической сети:

а — разомкнутая сеть; б — замкну- тая сеть

ассивные элементы схем замещения (сопротивления и проводимости) создают пути для прохождения элек-

трических токов. Пассивные элементы (ветви) электри­- ческих систем обычно разделяют на продольные и по­- перечные.

Поперечные пассивные элементы — это ветви, включен- ные между узлами схемы и нейтралью, т. е. узлом, имею­- щим напряжение, равное нулю. На рис. В.3, а нейтраль— это узел О. На рис. В.3, б этот же узел — земля. Продоль­- ные элементы — это ветви, соединяющие все узлы, кроме узла с напряжением, равным нулю, т. е. продольные ветви не соединены с нейтралью. Продольные ветви включают ак- тивные и индуктивные сопротивления линий электропереда­- чи ( на рис. В.3, а, б) и обмоток трансформаторов, ем­- кость устройств продольной компенсации. Поперечные пас- сивные элементы соответствуют проводимостям линий электропередачи на землю, реакторам и конденсаторам, включенным на землю. В некоторых случаях потери в стали трансформаторов представляются в схеме замещения как поперечные проводимости.

Активные элементы схем замещения — источники ЭДС и тока. Для них наиболее характерным является то, что они определяют напряжение или токи в точках присоеди­- нения этих элементов в соответствующей цепи независимо от ее остальных параметров. Источники ЭДС в расчетах электрических систем используются редко. Поэтому ниже в основном речь будет идти об источниках тока.

Источники тока в расчетах электрических систем соот­- ветствуют нагрузкам потребителей и генераторов электри­- ческих станций. Именно в этих активных элементах потреб- ляется и генерируется мощность.

Уравнения установившегося режима. Установившиеся режимы цепей, содержащих только линейные пассивные элементы и постоянные не изменяющиеся по модулю и фа­- зе источники тока, описываются линейными алгебраически- ми уравнениями — линейными уравнениями установившего- ся режима. Такие цепи называются линейными электричес­- кими цепями. Этот случай соответствует расчету установившихся режимов электрических систем при зада­- нии постоянных по модулю и фазе токов нагрузки потре­- бителей и генераторов во всех узлах электрической систе­- мы, кроме одного.

В расчетах установившихся режимов электрических сис- тем нелинейность пассивных элементов, как правило, не учитывается. В этом смысле продольная часть схемы заме­- щения всегда линейна. В то же время, как правило, при расчетах установившихся режимов электрических систем учитываются нелинейные характеристики источников тока. Нелинейность источников тока соответствует заданию в уз­- лах нагрузки потребителей или генераторов с постоянной мощностью либо заданию нагрузки ее статическими харак­- теристиками, определяющими зависимость мощности от напряжения. Установившиеся режимы электрических сис­- тем с нелинейными источниками тока описываются нели­- нейными алгебраическими уравнениями — нелинейными уравнениями установившегося режима.

3.2. Расчет режима линии электропередачи

ПРИ ЗАДАННОМ ТОКЕ НАГРУЗКИ

Задано напряжение в конце линии . Известны (рис. 3.2, а) ток нагрузки , напряжение , сопротивление и проводимость линии , . Надо определить напряжение , ток в продольной части линии , потери мощности в линиии ток .

Расчет состоит в определении неизвестных токов и на- пряжений последовательно от конца линии к началу. Для определения токов и напряжений применяются первый за­- кон Кирхгофа и закон Ома.

Будем использовать фазные напряжения и токи .Емкостный ток в конце линии 12, соединяющей узлы 1 и 2,

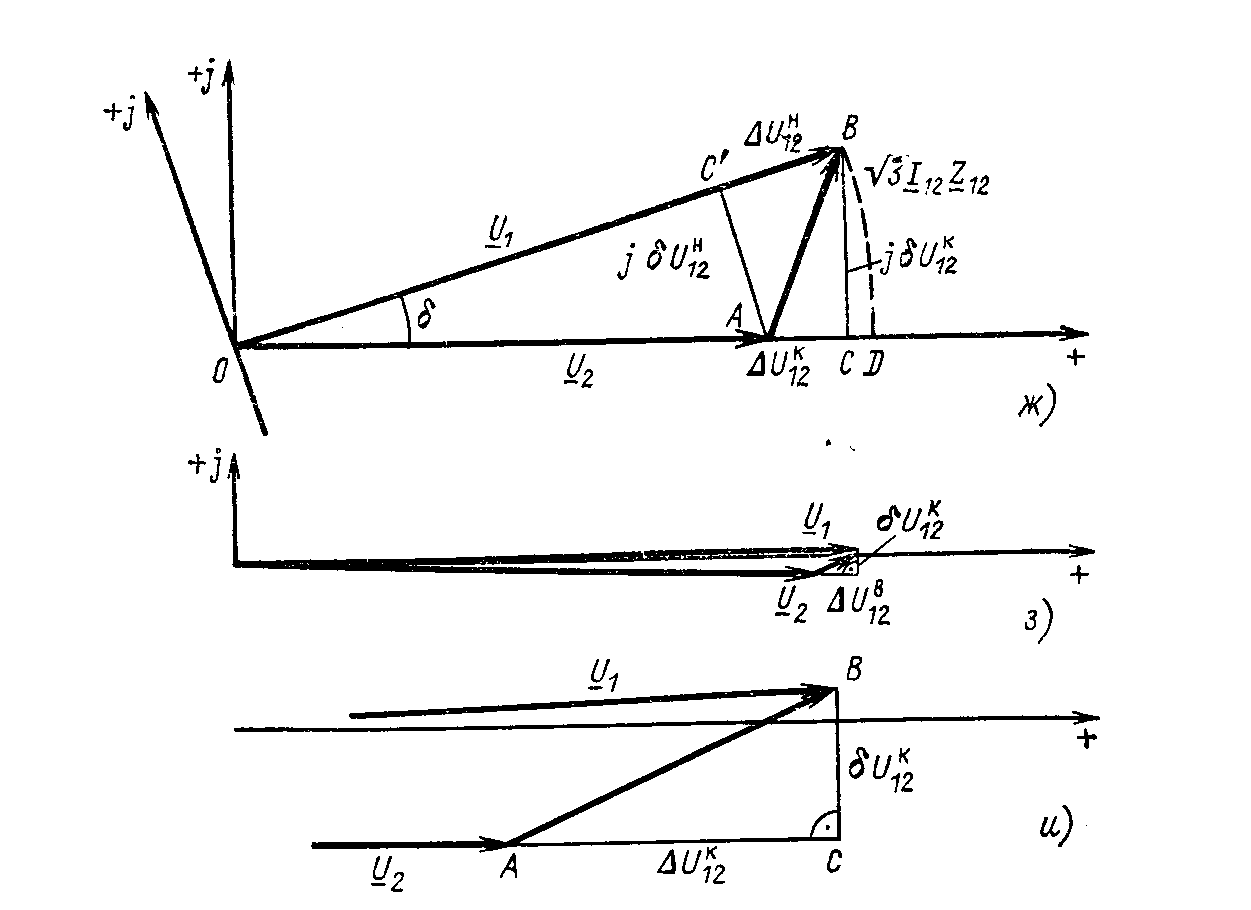
Рис. 3.2. Расчет режима линии электропередач:

а—схема замещения; б—определение емкостного тока; в—векторная диаграмма для линии с нагрузкой; г — векторная диаграмма для линии на холостом ходу; д—схема замещения линии для расчета при заданной мощности нагрузки; е— векторная диаграмма напряжений в начале и в конце линии при расчете по данным конца; ж—векторная диаграмма линейных напряжении в начале и в конце линии при расчете по данным начала; з—векторная диаграмма к примеру 3.2; и—уве­- личенное изображение составляющих падения напряжения для диаграммы з

по закону Ома (рис. 3.2, б)

. (3.1)

Ток в продольной части линии 12 по первому закону Кирхгофа

. (3.2)

Напряжение в начале линии по закону Ома

. (3.3)

Емкостный ток в начале линии

. (3.4)

Ток в начале линии по первому закону Кирхгофа

. (3.5)

Потери мощности в линии (в трех фазах)

. (3.6)

Векторная диаграмма токов и напряжений (рис. 3.2,в) строится в соответствии с выражениями (3.1)—(3.5). Вна­- чале строим на диаграмме известные и . Полагаем, что , т.е. напряжение направлено по дейст­вительной оси. Емкостный токопережает¹ на 90° напряжение . Ток соединяет начало первого и конец второго суммируемых векторов в правой части (3.2). Затем строим отдельно два слагаемых в правой час­ти (3.3):

. (3.7)

Вектор параллелен . Вектор опережает на 90° ток . Напряжение соединяет начало и конец сум- мируемых векторов , , . Ток опережает на 90°, соответствует (3.5).

В линии с нагрузкой напряжение в конце по модулю меньше, чем в начале, (рис. 3.2,в).

В линии на холостом ходу, т. е. при токе нагрузке , течет только емкостный ток, так как в соответствии с (3.2)

, (3.8)

В этом случае напряжение в конце линии повышается: . Векторная диаграмма токов и напряжений для такой линии приведена на рис. 3.2, г.

Задано напряжение в начале линии . Извест­- ны , ,, . Надо определить , , , . В дан- ном случае невозможно, как ранее последовательно от кон- ца линии к началу определить неизвестные токи и напря- жения, используя первый закон Кирхгофа и закон Ома.

Рассчитать режим очень легко, если использовать из- вестное уравнение узловых напряжений (узловых потен­- циалов) для узла 2:

, (3.9)

где — взаимная (или общая) проводимость узлов 1 и 2, равная сумме проводимостей ветвей, соединяющих эти уз­- лы и взятых с обратным знаком; —собственная прово­- димость узла 2, равная сумме проводимостей ветвей, со­- единенных с узлом 2. Для линии на рис. 3.2, а и б

; . (3.10)

Из уравнения узловых напряжений (3.9) легко опреде­- лить напряжение:

, (3.11)

а затем по закону Ома из (3.3) найти ток в линии , а из (3.5), (3.4) —ток.

Уравнение узловых напряжений (3.9) следует из перво­- го закона Кирхгофа.

Последовательное от конца линии к началу определение токов и напряжений по первому закону Кирхгофа и закону Ома можно применять только при расчетах разомкнутых сетей. Определение напряжений из уравнений узловых на­- пряжений и затем токов в линиях по закону Ома можно использовать для любых сетей — как для замкнутых, так и для разомкнутых.