2.5. Логический квадрат

Простые суждения, имеющие одинаковые термины (субъект и предикат) и различающиеся по качеству и по количеству, находятся в определенных отношениях по истинности и ложности, которые иллюстрируются с помощью логической схемы (логического квадрата).

Устанавливать типы отношений между суждениями по логическому квадрату важно при сопоставлении разных точек зрения по спорным вопросам в процессе дискуссии, редактировании текстов и в других случаях.

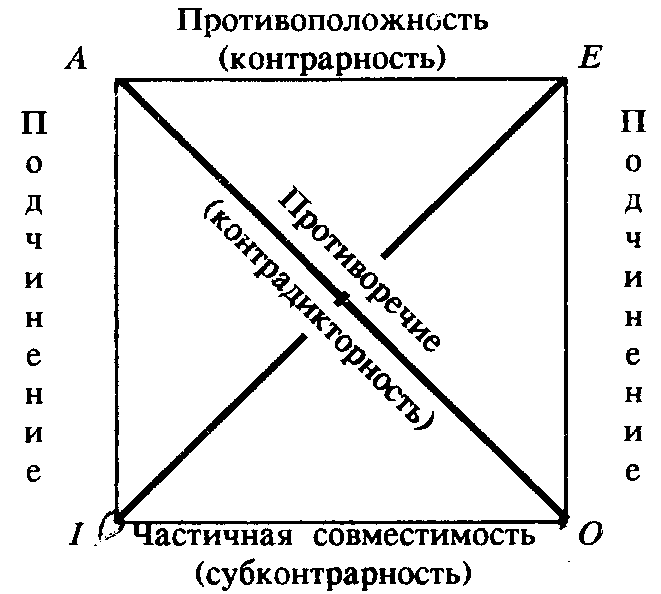
Отношения противоречия (контрадикторности): А—О, Е—I. Эти суждения не могут быть одновременно истинными и ложными. Из истинности одного суждения следует ложность другого, из ложности одного — истинность другого. Выводы строятся по схемам:     А_и — О_л, А_л — О_и, Е_и — I_л,    Е_л — I_и.

Отношения противоположности (контрарности): А — Е. Противоположные суждения не могут быть одновременно истинными, но могут быть одновременно ложными. Из ложности одного суждения следует истинность другого, но из истинности одного из них может следовать как истинность, так и ложность другого суждения.

Выводы строятся по схемам: А_и—Е_л, Е_и—А_л, А_л—Е?, Е_л — А?

Отношение частичной совместимости (субконтрарности): I — О. Эти суждения могут быть одновременно истинными, но не могут быть одновременно ложными. Из ложности одного суждения следует истинность другого, но из истинности одного из них может следовать как истинность, так и ложность другого. Выводы строятся по схемам: I_л — O_и, О_л — I_и, I_и — О?, О_и —I?

Отношение подчинения: А—I, Е—О. Из истинности подчиняющего суждения следует истинность подчиненного суждения, но не наоборот: из истинности подчиненного суждения истинность подчиняющего суждения не следует, оно может быть истинным, но может быть и ложным. Из ложности подчиненного суждения следует ложность подчиняющего суждения, но не наоборот: из ложности подчиненного суждения следует ложность подчиняющего суждения.

2.6. Сложные суждения

Суждения, состоящие более чем из одного простого суждения, называются сложными.

Сложные суждения, образованные посредством связи двух или нескольких простых суждений логическим союзом «и», называются соединительными (конъюнктивными). Логический союз «и» и равнозначные ему слова и союзы обозначаются знаком «». Например, «На улице холодно и идет дождь». Зависимость истинности конъюнктивного суждения от истинности исходных суждений можно изобразить в виде следующей таблицы истинности:

А	В	А  В
И	И	И
И	Л	Л
Л	И	Л
Л	Л	Л

где И — значение «истинно», Л — значение «ложно».

Сложные суждения, образованные посредством связи двух или нескольких простых суждений логическим союзом «или», называются разделительными (или дизъюнктивными).

Например: «Истец вправе увеличить или уменьшить размер исковых требований». Дизъюнктивная связь выражается также союзами «либо», «а также», «равно» и т.п., равнозначными по смыслу союзу «или».

Существует два вида разделительного союза «или»:

а) соединительно-разделительный — там, где возможные мыслимые признаки предметов не исключают друг друга. Например: «Некоторые продукты используются в пищу в соленом, копченом, консервированном или свежем виде». Обозначаются знаком «V» — простая дизъюнкция;

б) исключающе-разделительный — в данном случае возможные признаки предметов исключают друг друга. Например: «На очередных выборах победят либо республиканцы, либо демократы». Обозначается — «V » — строгая дизъюнкция. Простую и строгую дизъюнкцию можно выразить в виде следующих таблиц истинности:

а) простая дизъюнкция;

А	В	А V В
И	И	И
И	Л	И
Л	И	И
Л	Л	Л

б) строгая дизъюнкция.

А	В	А V В
И	И	Л
И	Л	И
Л	Л	И
Л	Л	Л

Сложные суждения, образованные посредством связи простых суждений с помощью союза «если ... то», называются условными или импликативными. Импликация обозначается — « ». Например: «Если на улице идет дождь, то асфальт мокрый». Таблица истинности для импликации:

А	В	А В
И	И	И
И	Л	Л
Л	И	И
Л	Л	И

Сложные суждения, связанные между собой с помощью союзов «если и только, если», «тогда и только тогда» и т.п., называются суждениями тождества или эквивалентности. Обозначается данный логический союз с помощью знака « ». Таблица истинности для суждений тождества или эквивалентности:

А	B	А В
И	И	И
И	Л	Л
Л	И	Л
Л	Л	И

В научном познании важно проводить различие между достаточными и необходимыми условиями наступления какого-то факта, события, отражаемого в условном суждении.

Условия являются достаточными, если при их выполнении всегда наступает данное событие.

Условия являются необходимыми, если без их выполнения данное событие никогда не наступает.

Так, в импликативном суждении А В суждение А является достаточным условием для В, а В— необходимым условием для А.

Раздел 3. Умозаключение

3.1. Непосредственные умозаключения

3.2. Простой категорический силлогизм

3.3. Условные силлогизмы

3.4. Разделительный силлогизм

3.5. Энтимема

Форма мышления, посредством которой выводится новое суждение на основании одного или более известных суждений, называется умозаключением.

Если понятия – атомы, а суждения – молекулы нашей умственной деятельности, то, завершая эту аналогию, можно сказать, что умозаключения – это и есть сама умственная деятельность. Рассуждать, задавать вопросы, искать ответы, предсказывать, доказывать, опровергать, убеждать и подвергать сомнению – все эти и другие формы мыслительной деятельности имеют вид определенных умозаключений. Мы вправе, поэтому, утверждать, что мыслить и делать умозаключения – это одно и то же.

Умозаключения делятся на следующие основные виды: дедуктивные и индуктивные.

Умозаключение называется дедуктивным (лат. deductio), если между его посылками и заключением имеет место отношение логического следования.

В дедуктивных умозаключениях, если посылки истинны и при этом соблюдены соответствующие правила логики, то заключение будет истинным.

Умозаключение называется индуктивным, если между его посылками не имеется отношения логического следования.

В индуктивных умозаключениях процесс рассуждения направлен от частного к общему.

Итак, умозаключение — это форма мышления, посредством которой из одного или нескольких суждений с необходимостью выводится суждение, заключающее в себе новое знание.

Суждения, из которых делается вывод, называется посылками умозаключения. Суждение, являющееся выводом умозаключения, называется заключением.

Пример:

Все жидкости — упруги.

Ртуть — жидкость.__________

Следовательно, ртуть — упруга.

В этом умозаключении из двух посылок - «Все жидкости — упруги» и «Ртуть — жидкость» - выводится заключение: «Ртуть — упруга», в котором содержится новое знание.

Логичность наших рассуждений в значительной мере зависит от того, насколько умело мы пользуемся умозаключениями. Когда говорят о «железной логике» рассуждения, то имеют в виду, прежде всего, такую его особенность, когда одно положение с необходимостью следует из другого.