Расчет и построение переходной характеристики сар.
Представим ВЧХ в виде суммы трапециидальных характеристик рис.5.
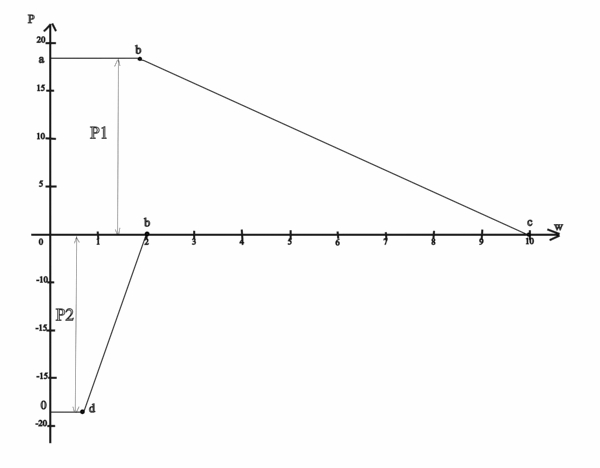
рис.5.
Параметры трапециидальных характеристик:
трапеция oabc: Р1=18.3; d1=2; k1=10; æ1=d1/k1=0.2;
трапеция abdo: P2=-18.3; d2=0.7; k2=2; æ2=d2/k2=0.35;
Для каждой из трапеций определим переходной процесс, для этого по вычисленным значениям параметра æ входим в таблицу h функций и определяем переходные характеристики (h-функции) единичных трапеций, которые соответствуют неединичным по параметру æ. Произведем пересчет реального времени t, и фактической ординаты переходных характеристик для каждой из неединичных трапеций, а результаты поместим в таблицу:
-
æ1=0.2
k1=10
P1=18.3
æ1=0.35
k2=2
P2=-18.3
h1’
t=/k1
X1=P1h1’
h2’
t=/k2
X2=P2h2’
X=X1+X2
0
0
0
0
0
0
0
0
0.5
0.192
0.05
3.5
0.215
0.25
-3.9
-0.39
1
0.371
0.1
6.4
0.417
0.5
-7.6
-1.23
1.5
0.538
0.15
9.8
0.603
0.75
-11
-1.2
2
0683
0.2
12.5
0.761
1
-13.9
-0.4
2.5
0.867
0.25
15.9
0.891
1.25
-16.3
-1.4
3
0.896
0.3
16.4
0.987
1.5
-17.9
-1.5
3.5
0.963
0.35
17.6
1.050
1.75
-19.2
-1.6
4
1.008
0.4
18.4
1.090
2
-20
-1.6
4.5
1.029
0.45
18.8
1.100
2.25
-20.1
-1.3
5
1.042
0.5
19
1.103
2.5
-20.2
-1.2
5.5
1.046
0.55
19.1
1.093
2.75
-20
-0.9
6
1.037
0.6
19
1.070
3
-19.6
-0.6
6.5
1.030
0.65
18.8
1.049
3.25
-19.2
-0.4
7
1.024
0.7
18.7
1.033
3.5
-18.9
-0.2
7.5
1.019
0.75
18.6
1.017
3.75
-18.6
0
8
1.020
0.8
18.6
1.012
4
-18.5
0.1
8.5
1.021
0.85
18.7
1.007
4.25
-18.4
0.3
9
1.025
0.9
18.7
1.006
4.5
-18.4
0.3
9.5
1.029
0.95
18.8
1.006
4.75
-18.4
0.4
10
1.031
1
18.9
1.006
5
-18.4
0.5
10.5
1.033
1.05
18.9
1.005
5.25
-18.4
0.5
11
1.031
1.1
18.9
1.002
5.5
-18.3
0.6
11.5
1.028
1.15
18.8
0.999
5.75
-18.3
0.5
12
1.024
1.2
18.7
0.994
6
-18.2
0.5
12.5
1.019
1.25
18.6
0.990
6.25
-18.1
0.5
13
1.015
1.3
18.6
0.986
6.5
-18
0.6
По данным таблиы строим графики переходных процессов. X(t) – график переходного процесса САР рис.6.
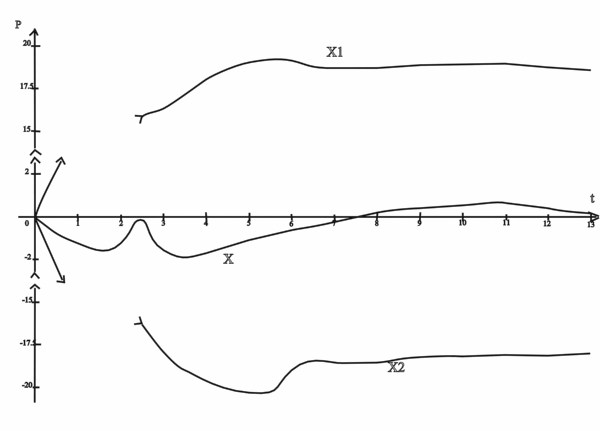
рис.6.