Методические указания к задаче 2.

Все расчеты [5] производить в долевых (относительных) единицах (д.е.), согласно которым принимать:

Единица напряжения - номинальное фазное напряжение.

Единица тока нагрузки - номинальный ток фазы.

Единица мощности - номинальная кажущаяся мощность.

Единица сопротивления - определяется единицами напряжения и тока.

Единица тока возбуждения или намагничивающей силы - ток возбуж­дения или намагничивающая сила, соответствующие номинальному напряжению при холостом ходе.

К п. 1. Для построения характеристики холостого хода сле­дует использовать данные таблицы нормальной характеристики.

Таблица нормальной характеристики (вд.е.)

I_в д.е 0 0,5 1,0 1,5 2,0 2,5

д.е 0 0,58 1,0 1,23 1,3 1,35

Характеристику короткого замыкания построить по заданной величине ОКЗ, имея в виду, что ОКЗ равно величине тока коротко­го замыкания в д.е. при единичном токе возбуждения [3, §9.5].

Ненасыщенное значение продольного синхронного сопротивления следует найти, пользуясь "ненасыщенной" характеристи­кой холостого хода (продолженная прямая часть характеристики) и характеристикой короткого замыкания [3,§ 9.5].

Зная , найти

= , а затем, учитывая при этом, что

.

В [3, §9.4] Kобозначены соответственноKd,Kq - коэффициенты реакции якоря.

Величину м.д.с. реакции якоря F_а при номинальном токе проще всего найти, построив треугольник короткого замыкания (реактивный треугольник) [3, §9.5].

К п. 2. Векторную диаграмму явнополюсного генератора можно построить в соответствии с рекомендациями, приведенными в [3, § 9.5]:

а) построить вектор 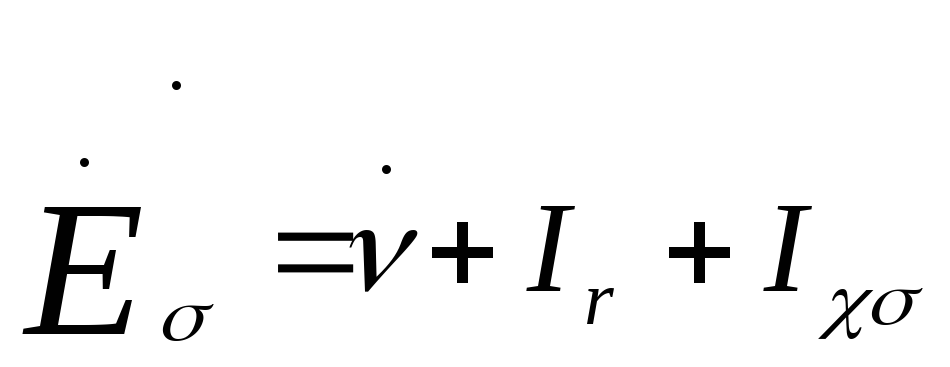и прибавить к нему вектор. Так определяется угол и направление э.д.с воз­буждения ;

E (в [2, §9.5] -E) – э.д.с., индуктируемая в об­мотке якоря потоком рассеяния; эту э.д.с. можно представить в виде суммы двух составляющих , ориентированных по осям d-d и q-q:

;

б) найти проекцию вектора на направление э.д.с. воз­буждения - вектор . Определить величину возбуждения, со­ответствующего э.д.с.Ed-по характеристике холостого хода;

в) найти продольную составляющую тока нагрузки Id=sin и соответствующую ей продольную м.д.с. реакции якоря Fad=Fasin ;

г) ток возбуждения при номинальном режиме равен

i_вн=id+F_ad(д.е);

д) току возбуждения i_вн соответствует э.д.с. E₀ и повы­шение напряжения при сбросе нагрузки;

е) насыщенное значение продольного реактивного сопротивле­ния реакции якоря можно определить так:

отсюда

K п. 3. При построении диаграммы э.д.с. принять реактивное сопротивление равным.

К п. 4. Токи возбуждения, необходимые для построения регулировочных характеристик, определить из диаграммы э.д.с. [3, §9.5]. Каждую регулировочную характеристику построить по четы­рем точкам, определенным для значений тока нагрузки, равных 0; 0,5; I; 1,3; д.е. [2, §9.6].

Внешнюю характеристику генератора построить для номинального коэффициента мощности и тока возбуждения номинального режима. Поэтому две точки определяются по регулировочным характеристи­кам для V = 1,1 и V = 1,2.

К п. 5. Для построения угловой характеристики использовать уравнение мощности синхронной машины [3, § 9.8]. В д.е. это уравнение имеет следующий вид:

P=

Следует иметь в виду, что при изменении угла изменяет­ся магнитный поток продольной оси, а следовательно, и насыщение. Поэтому одному и тому же значению тока возбуждения могут соот­ветствовать различные значения. Для того, чтобы упрос­тить построение угловой характеристики, воспользуемся тем, чтофизически соответствует току короткого замыкания (при токе возбуждения номинального режима). Таким образом, приблизительно примем:

отсюда P=[i_внsin +]*ОКЗ д.е

отношение следует взять из решения п.1.

Для построения угловой характеристики рассчитать для следующих значений угла °: 30°, 60°, 90°, 120°, 150°.

К п. 6. Для построения V - образных характеристик (зави­симостей тока якоря от тока возбуждения) [3, §9.9], использо­вать упрощенные векторные диаграммы [3, §9.5], пренебрегая падениями, напряжения Ir и jIx2 . В этом случае = , поэтому ток возбуждения определяется векторной суммойIв = 1 и реакцией и якоря, определяемой током нагрузки. Следует помнить, что при токе нагрузки, равном I д.е. реакция якоря равна Fa д.е (смотрите решение п.1). Для случая P = 0 векторная сумма прев­ращается в алгебраическую. В случае Р = 0,75 V - образная характеристика строится для постоянной активной составляющей тока нагрузки, равной:

Ia=Pcosд.е

К п. 7. Для решения задачи необходимо разложить несимметричную трехфазную систему токов нагрузки ( Ia=I, Iв=-I, Ic=0 ) на симметричные составляющиеI₁, I₂,I₀ ( в данном частном случае I₀=0 ). Э.д.с. фазы А принять равной величине, най­денной в решении п.2. Э.д.с. трех фаз образует симметричную трехфазную систему. Фазовые значения напряжения найдем, вычитая из фазовых э.д.с. падения напряжения прямого и обратного следования:

Аналогично проводятся расчеты для фаз B и С. При этом в ка­честве реактивного сопротивления принять насыщенное значе­ние , определенное в п.2.

Коэффициентом асимметрии % называется отношение напря­жения обратного следования к напряжению прямого следования:

Вариант №3

Задача 1. Сельсины.

В синхронной передаче применены одинаковые контактные

самосинхронизирующиеся сельсины, которые имеют данные согласно

таблицы 5.

Требуется:

1. Определить минимальный угол рассогласования, необходимый для преодоления момента сопротивления (трения) на валу приемника. Момент сопротивления нагрузки приемника равен нулю.

2. Определить угол рассогласования синхронной передачи, работа­ющей в режиме вращения при заданном отношении , где- скорость вращения ротора, - синхронная скорость.

3. Определить коэффициент рассеяния .