10. Скалярное произведение двух векторов
10.1. Определение скалярного произведения
Определение 19.
Скалярным
произведением векторов
и
называется число, равное произведению
их длин на косинус угла между ними и
обозначается
:
.
Если известны
скалярное произведение векторов
,
и их длины
,
,
то угол между векторами (косинус угла
между векторами) вычисляют по формуле
.
Если известны координаты векторов:
, ,
то скалярное произведение вычисляется по формуле
,
а косинус угла – по формуле
.
10.2. Свойства скалярного произведения
Свойство 1.
– закон коммутативности.
Свойство 2.
– закон ассоциативности.
Свойство 3.
– закон дистрибутивности.
Свойство 4.
;
для того чтобы два вектора были
перпендикулярны, необходимо и достаточно,
чтобы их скалярное произведение равнялось
нулю.
Свойство 5.
;
скалярный квадрат вектора равен квадрату
его длины.
11. Векторное произведение двух векторов
11.1. Определение векторного произведения
Определение 20. Векторным произведением векторов на вектор называется вектор , такой, что:
1) его длина равна площади параллелограмма, построенного на векторах и :
;
2) он перпендикулярен каждому из перемножаемых векторов:
;
3) направление вектора определяется по правилу «правой тройки», то есть кратчайший поворот от вектора (первого множителя) к вектору (второму множителю) из конца вектора виден против хода часовой стрелки.
Векторное
произведение
и
обозначается
.
Если известны координаты векторов:
, ,
то векторное произведение вычисляется по формулам:
,
.
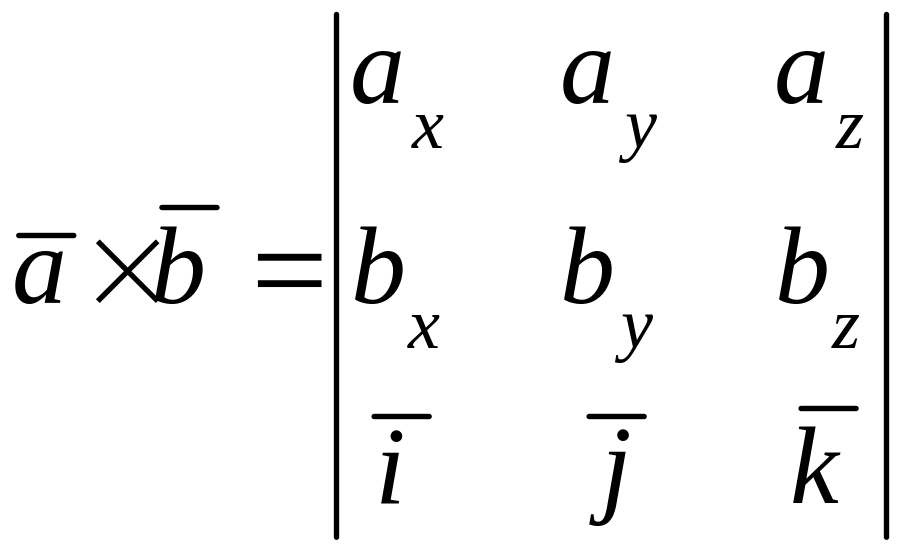11.2. Свойства векторного произведения
Свойство 1.
– закон антикоммутативности.
Свойство 2.
– закон ассоциативности.
Свойство 3.
– закон дистрибутивности.
Свойство 4.
;
для того чтобы два вектора были параллельны
(коллинеарны), необходимо и достаточно,
чтобы их векторное произведение равнялось
нулю.
Свойство 5.
;
векторный квадрат вектора равен нулевому
вектору.
Свойство 6. Геометрический смысл векторного произведения: длина векторного произведения векторов и равна площади параллелограмма, построенного на этих векторах (пункт 1) определения).
12. Смешанное произведение трёх векторов
12.1. Определение смешанного произведения
Определение 21.
Смешанным
произведением трёх векторов
,
и
называется число, скалярному произведению
первого вектора на векторное произведение
двух других. Смешанное произведение
векторов
,
и
обозначается
.
Таким образом,
.
В определении смешанного произведения можно векторно умножить вектор на вектор , а затем полученный вектор скалярно умножить на вектор .
Если известны координаты векторов:
,
,
,
то векторное произведение вычисляется по формулам:
,
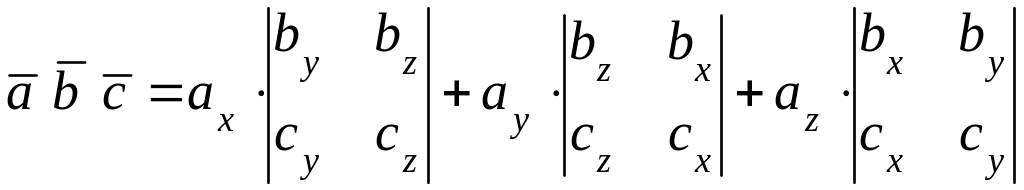12.2. Свойства смешанного произведения
Свойство 1.
;
.
Свойство 2. Геометрический смысл векторного произведения: модуль смешанного произведения векторов , и равен объёму параллелепипеда, построенного на этих векторах.
Векторы, параллельные одной плоскости, называются компланарными. Для любых двух векторов найдется плоскость, параллельная этим векторам. Поэтому, два вектора всегда компларны. Три и более количество векторов могут быть параллельными одной плоскости, и могут не быть параллельными. Следующее свойство даёт ответ на вопрос: является ли данная тройка векторов компланарной?
Свойство 3.
– компланарные; для того чтобы три
вектора принадлежали одной плоскости,
необходимо и достаточно, чтобы их
смешанное произведение равнялось нулю.