4. Единичный вектор
Определение 9. Любой вектор, длина которой равна единице, называется единичным вектором.
Пусть задан вектор
.
Обозначим через
единичный вектор, сонаправленный с
вектором
.
Из определения умножения вектора на
число следует, что
или
.
Для каждой числовой
оси
определен единичный вектор
,
с началом в точке
(
– центр числовой оси) и концом в точке
с координатой
(рис. 12). Направление единичного вектора
совпадает с положительным направлением
числовой оси
.
Рис. 12
5. Угол между векторами
Определение 10.
Пусть векторы
и
имеют общее начало. Углом
между векторами
и
называется наименьший угол
,
на который нужно повернуть один из этих
векторов до совпадения с другим (рис.
13). Под термином совпадение понимается,
что векторы
и
окажутся сонаправленными. Угол между
векторами
и
обозначают
.
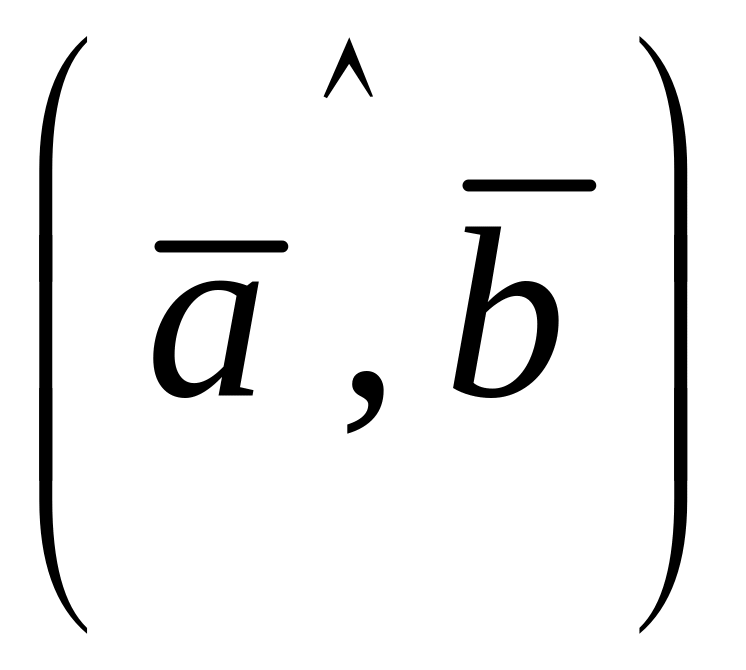Из определения
вытекает, что угол
между произвольными векторами содержится
в промежутке:
.
Определение 11. Пусть начало вектора находится в центре числовой оси . Углом между вектором и осью называется угол между вектором и единичным вектором оси (рис. 14).
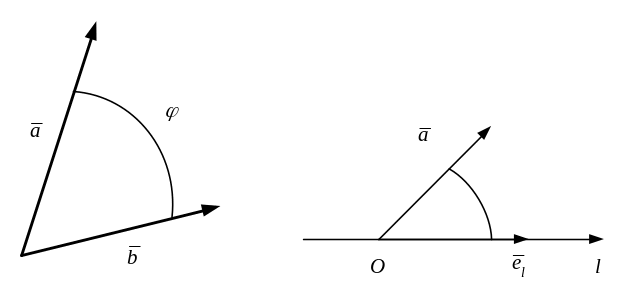
Рис. 13 Рис. 14
6. Проекция вектора на ось
Определение 12.
Проекцией
точки
на ось
называется точка пересечения плоскости
,
проходящей через точку
перпендикулярно оси
с осью
(рис. 15).
Рис. 15
Определение 13. Проекцией вектора на ось называется число, равное разности координат проекций конца и начала (рис. 16).
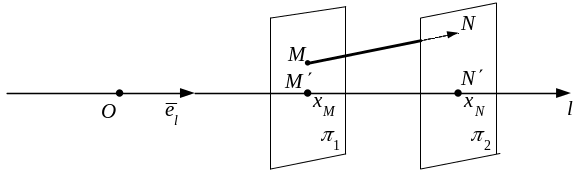
Рис. 16
Проекция вектора
на ось
обозначается
.
Имеем
.
Обозначим через угол между вектором и осью .
Проекция вектора
может быть: 1) положительной, если угол
острый. В этом случае
(рис 16), 2) отрицательной, если угол
тупой. В этом случае
(рис. 17), 3) нулевой, если угол
или
.
В этом случае
(рис. 18).
Рис. 17 Рис. 18
Определение 13.
Составляющей
вектора
по оси
называется произведение проекции
вектора
на ось
на единичный вектор
этой оси и обозначается
.
Составляющей вектора по оси есть вектор, соединяющий проекцию начала и проекцию конца вектора:
.
Отметим некоторые свойства проекции вектора на ось.
Свойство 1. Проекция вектора на ось равна произведению длины вектора на косинус угла между вектором и осью :
.
Свойство 2. Проекция произведения вектора на число на ось равна произведению числа на проекцию вектора на ось :
.
Свойство 3. Проекция суммы двух векторов и на ось равна сумме проекций этих векторов на ось :
.
Свойство 4. Проекция разности двух векторов и на ось равна разности проекций этих векторов на ось :
.
7. Системы координат
7.1. Декартова система координат на плоскости
Определение 14. Прямоугольной системой координат на плоскости называется пара взаимно перпендикулярных числовых осей, имеющие общее начало . Общее начало совпадает с точкой пересечения (рис. 19).
Определение 15.
Плоскость в которой, расположены оси,
называется координатной
плоскостью
.
Осей, составляющих
прямоугольную систему координат на
плоскости обозначим
и
.
Как правило, ось
на чертеже располагают горизонтально,
а ось
– вертикально. Произвольной точке
плоскости соответствуют два вещественных
числа (рис. 20):
1) проекция точки на ось и обозначают ;
2) проекция точки
на ось
и обозначают
.
Рис. 19 Рис. 20
Определение 16. Число называется абсциссой точки , число – ординатой этой точки.
Определение 17. Ось называется осью абсцисс, ось – осью ординат.
Определение 18.
Упорядоченная пара чисел
называется прямоугольными
(декартовыми)
координатами
точки
координатной плоскости
и обозначается
.
Каждой точке координатной плоскости соответствует единственная упорядоченная пара чисел и, наоборот, каждой упорядоченной паре чисел соответствует единственная точка координатной плоскости .
Координатные оси и делят координатную плоскость на четыре четверти (на четыре квадранты). Каждая точка , не принадлежащая координатным осям, содержится в одной из четырех четвертей. Обозначение этих четвертей и знаки координат точки:
1) первая четверть
–
;
;
2) вторая четверть
–
;
;
3) третья четверть
–
;
;
4) четвёртая четверть
–
;
.