
- •Раздел 1. Гидромеханика.
- •Глава 1. Основные физические свойства жидкости.
- •1.1. Общие положения.
- •1.2. Силы, действующие на жидкий объем.
- •1.3. Вязкость.
- •Глава 2. Основы гидромеханики.
- •2.1. Основные уравнения гидромеханики.
- •2.2. Частные случаи уравнения Навье-Стокса.
- •2.3. Основные уравнения гидростатики.
- •2.4. Кинематика жидкости.
- •Уравнение неразрывности потока
- •Гидродинамический напор
- •2.4.1. Уравнение Бернулли для идеальной несжимаемой жидкости.
- •2.4.2. Уравнение Бернулли для потока реальной (вязкой) жидкости .
- •Напорная и пьезометрическая линии
- •Связь давления и скорости в потоке
- •Глава 3. Режимы течения жидкости.
- •3. Ламинарное течение жидкости.
- •3.1. Ламинарное течение в каналах круглого сечения. ( Течение Пуазейля-Гагена ).
- •Распределение касательных напряжений.
- •Зависимость между перепадом давления и расходом
- •Коэффициент Кориолиса в общем случае равен:
- •3.2. Ламинарное течение в зазоре между параллельными пластинами (Течение Куэтта).
- •Частные случаи течения Куэтта.
- •3.3. Течение жидкости в кольцевых зазорах.
- •3.4. Течение в гидродинамических опорах скольжения (элементы гидродинамической теории смазки гтс).
- •3.5. Течение жидкости в гидростатических опорах и подшипниках скольжения.
- •3.5.1. Гидростатическая опора поршня насоса с круглой камерой и частичной разгрузкой сопряженных поверхностей.
- •3.5.2. Гидростатический подшипник с полной разгрузкой сопряженных поверхностей.
- •Глава 4. Турбулентное течение.
- •4.1. Общие положения.
- •4.2. Поле осредненных скоростей.
- •4.3. Потери напора в трубах.
- •4.3.1. Потери на трение в круглых трубах при ламинарном течении.
- •4.3.2. Потери на трение в круглых трубах при турбулентном течении.
- •4.3.3. Потери на трение в шероховатых круглых трубах и некруглых руслах.
3.2. Ламинарное течение в зазоре между параллельными пластинами (Течение Куэтта).
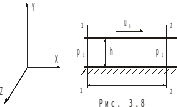
Условия практически те же, что и для течения Пуазейля-Гагена.
Отличия:
1). Одна из стенок подвижна.
2). Задача неосесимметричная, а плоская.
Таким образом, полученное в предшествующем разделе уравнение
преобразуется к следующему виду:
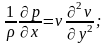 так
как
так
как
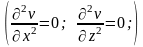
Как и в предыдущем случае:
Таким образом, получаем дифференциальное уравнение:
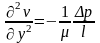
После интегрирования получим:
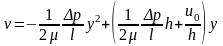
или
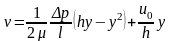
Расход жидкости через плоскую щель при ее ширине равной - b
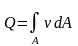
В
данном случае:
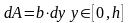
Таким
образом:
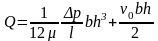
Распределение касательных напряжений.
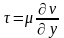 ,
,
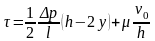
Принимая y=h мы можем получить касательные напряжения на движущейся пластине.
Это позволяет определить силу вязкого трения, которое в общем случае определяется по следующей зависимости:
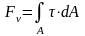
Течение Куэтта можно рассматривать как суперпозицию двух течений: течения под действием перепада давления и фрикционного течения, вызванного движением одной из пластин.
Частные случаи течения Куэтта.
а).
Чистый сдвиг
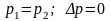 (рис.3.6.)
(рис.3.6.)
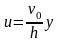 ,
,

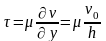
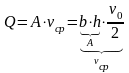
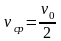 ,
,
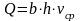 ,
,
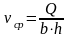
б). Течение между неподвижными пластинами.(рис.3.7)
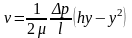 ,
,
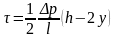
Отсюда
следует, что:
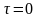 при
при
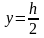
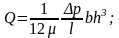
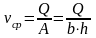 ;
;
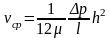
в

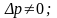 При
При
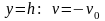
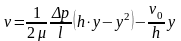 ;
;
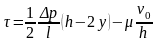 ;
;
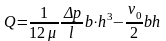 .
.
Для
обеспечения нулевого расхода, скорость
пластины должна быть: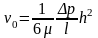 ,
,
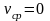
3.3. Течение жидкости в кольцевых зазорах.
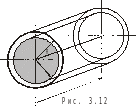
а). Концентричный зазор.(рис.3.9)
Внутренний и наружный цилиндры
неподвижны.
Кольцевую щель можно рассматривать
как щель с высотой h=R-r и шириной
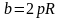 .
.
Поэтому для расчета параметров течения в кольцевых зазорах используется формула для параллельных пластин. В частности расход между неподвижными цилиндрами рассчитывается по зависимости:
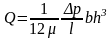
Или:
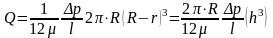
Окончательно:
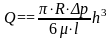
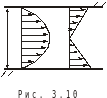
б). Эксцентричный зазор. (рис.3.10)
О

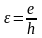 -
относительный эксцентриситет, где h
- радиальный зазор при концентричном
расположении
цилиндра.
-
относительный эксцентриситет, где h
- радиальный зазор при концентричном
расположении
цилиндра.
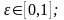
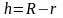
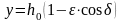
Расход через заштрихованную площадку
определяем по формуле для параллельных пластин:
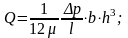
Для участка шириной db:
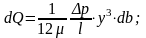
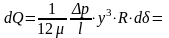
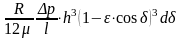
Полный
расход получаем интегрированием dQ
по углу
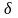 в пределах
в пределах
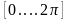 :
:
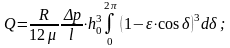
После интегрирования (без вывода) получаем:
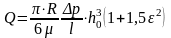
где Qэ - расход через эксцентричную щель,
Qс - расход через соосную щель.
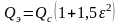
Если
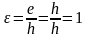 ,
то значение:
,
то значение:
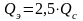
3.4. Течение в гидродинамических опорах скольжения (элементы гидродинамической теории смазки гтс).
Гидродинамическая теория смазки изучает течение жидкости в зазоре между двумя взаимодействующими сопряженными поверхностями твердых тел, разделенных слоем смазки.
В основе гидродинамической теории смазки лежат дифференциальные уравнения вязкой несжимаемой жидкости.
Рассмотрим уравнения движения жидкости применительно к двум взаимно перемещающимся плоскостям, зазор между которыми переменный. (рис.3.11)
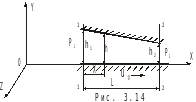
Будем считать, что величина зазора пропорциональна координате Х:
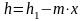 -
текущее значение зазора.
-
текущее значение зазора.
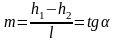 -
угловой коэффициент.
-
угловой коэффициент.
Для решения задачи следует учитывать следующее:
1).
Движение установившееся: все производные
по времени равны нулю:
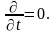
2). Пластины бесконечной ширины (b>4l), краевые эффекты не учитываются. Следовательно, все величины не зависят от Z.
3). В отличие от течения Куэтта толщина зазора изменяется вдоль оси X, то есть изменяется и скорость течения жидкости.
Следовательно,
конвективные ускорения
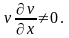
Непостоянен
и градиент давления
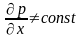 .
.
4).
Однако по толщине смазочного слоя
давление имеет одно и тоже значение
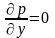 :
:
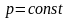
Кроме того, в основе предложенной Рейнольдсом гидродинамической теории смазки лежат следующие допущения:
1) массовыми силами пренебрегаем (X=Y=Z=0);
2)
смазка является ньютоновской жидкостью:
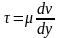 ;
;
3)
вязкость жидкости постоянна
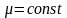 ;
;
4)
жидкость несжимаема
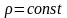 ;
;
5) толщина масляной пленки (зазора) мала по сравнению с другими геометрическими размерами: h<<l; h<<<b.
Согласно приведенным допущениям дифференциальное уравнение движения жидкости в зазоре может быть получено из уравнений Навье-Стокса так же как и в случае течения Куэтта.
Уравнение Навье-Стокса для несжимаемой жидкости:
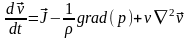
в проекции на ось X записывается:
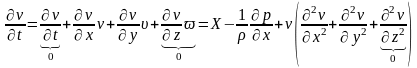
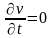 -
так как установившееся движение,
-
так как установившееся движение,
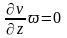 -
так как величины по Z не изменяются,
-
так как величины по Z не изменяются,
X=0 - пренебрегаем,
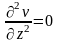 -
так как величины от Z
не зависят,
-
так как величины от Z
не зависят,
Таким образом, с учетом принятых допущений уравнение Навье-Стокса в проекции на ось X записывается:
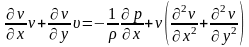 ,
домножив его на ρ
и выполнив преобразования получаем:
,
домножив его на ρ
и выполнив преобразования получаем:
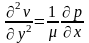
В отличие от уравнения Куэтта
Дважды интегрируя последнее дифференциальное уравнение получаем:
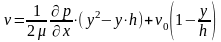
Таким образом, поле скоростей так же как и в течении Куэтта получается в результате наложения двух течений:
фрикционного
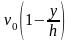
и вызванного перепадом давления.
Расход жидкости для единичной ширины гидродинамической опоры определиться по формуле:
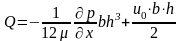
Распределение
давления по длине
неэквидистантного
зазора при безнапорном течении:
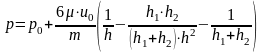 .
.
Полученная зависимость характеризует изменение давления в клиновом зазоре, которое создает подъемную силу.
Таким
образом, можно говорить о несущей
способности Fy
гидродинамической опоры:
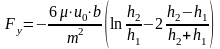
Силы трения в гидродинамической опоре
Другим
важным параметром гидродинамической
опоры является сила трения, которая в
общем случае определяется по следующей
зависимости:
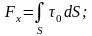
После
интегрирования 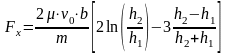
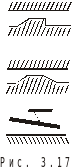
При h1=h2 теоретически нет подъемной силы Fy=0.
Но практически создается микродинамический эффект
обусловленный микронеровностями.
Микронеровности играют роль гидродинамических
клиньев. При этом давление не может опускаться
ниже “0”, но подниматься может существенно, что и
создает подъемную силу.
Гидродинамические опоры создаются с наклонными несущими поверхностями или самоустанавливающиеся:
Полученные выше результаты могут быть использованы для качественного объяснения основного эффекта смазки при вращении вала в подшипнике скольжения.
