3. Ламинарное течение жидкости.

Исследование течения жидкости в данном случае заключается в выводе и анализе зависимостей, характеризующих:

• закон распределения скорости по живому сечению потока,

• закон распределения касательных напряжений,

• связь между расходом жидкости и перепадом давления.

3.1. Ламинарное течение в каналах круглого сечения. ( Течение Пуазейля-Гагена ).

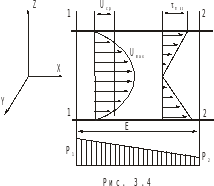
Здесь p₁ и р₂ - давления в сечениях 1 и 2.

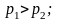
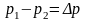
Как уже указывалось, установившееся течение вязкой несжимаемой жидкости описывается уравнением Эйлера:

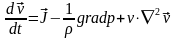
где 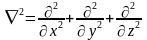- оператор Лапласа.

При рассмотрении ламинарного течения используются следующие допущения:

1. Течение - осесимметричное

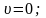
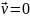
Таким образом, можно рассматривать уравнение Навье-Стокса только в проекциях на ось Х:

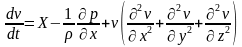
2. Течение - установившееся

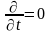
3. Силы тяжести - отсутствуют

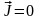
Из 2-го и 3-го допущений следует:

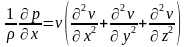
4. Труба постоянного сечения

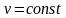
С учетом 4-го допущения в окончательном виде уравнение Навье-Стокса для установившегося осесимметричного течения можно записать:

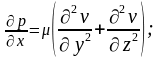
Для осесимметричного течения , что следует из рис.

и следовательно 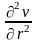- не зависит от х.

Таким образом, можно записать:

Здесь знак «-» потому, что давление уменьшается.

Таким образом, можно записать:

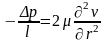
Или после преобразования:

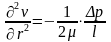
Теперь дважды интегрируя данное уравнение можем получить зависимость для распределения скорости по живому сечению потока.

Окончательно получаем:

Из полученного уравнения следует, что закон распределения скорости по живому сечению имеет параболический характер.

Из полученного уравнения следует, что максиальное значение скорость имеет в центре живого сечения потока:

При r=0:

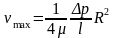
Распределение касательных напряжений.

Воспользуемся законом Ньютона для касательных напряжений, тогда:

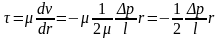
Отсюда следует, что касательное напряжение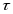 - имеет линейный закон распределения.

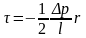
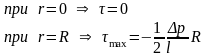
Графически распределение касательных напряжений по сечению потока показано на рис.

Зависимость между перепадом давления и расходом

Рис. 3.6

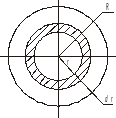
Из рис. 3.6 следует, что площадь элементарного кольцевого сечения определяется по следующей зависимости:

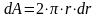
где:

Расход жидкости через живое сечение потока можно найти интегрируя скорость жидкости по данному сечению:

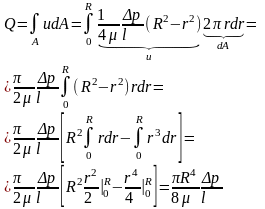
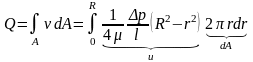
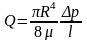
Учитывая, что R=d/2 получаем так называемую формулу Пуазейля-Гагена для трубы круглого сечения расход определиться как:

Связь между расходом Q и перепадом давления при ламинарном течении имеет линейный характер.

Тогда средняя скорость по сечению:

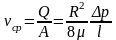
Как уже указывалось максимальное значение скорости рассчитывается по зависимости:

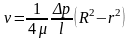
при r=0:

Сравнивая полученную зависимость с зависимостью для средней скорости, получаем:

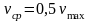
Коэффициент Кориолиса в общем случае равен:

Следовательно, производя подстановку ранее определенных значений, получаем, что коэффициент Кориолиса при расчете течения через кольцевой зазор α=2.

Полученные данные хорошо согласуются с опытными данными за исключением случаев:

- начального участка трубы, где происходит формирование профиля эпюры скоростей,

- течения с теплообменом ,

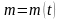- течения в капиллярах и зазорах с облитерацией,

- течения при больших перепадах давления.