Уравнение неразрывности потока

Уравнение неразрывности потока отражает закон сохранения массы: количество втекающей жидкости равно количеству вытекающей. Например, на рис. 8 расходы во входном и выходном сечениях трубы равны: q₁=q₂.

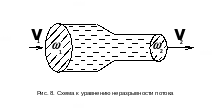
С учётом, что q=vω, получим уравнение неразрывности по­то­ка:

v₁ω₁ = v₂ω₂ .

А если выразим скорость для выходного сечения

v₂ = v₁ω₁/ω₂ ,

то можно заметить, что она увеличивается обратно пропорционально уменьшению площади живого сечения потока. Такая обратная зависимость между скоростью и площадью является важным следствием уравнения неразрывности и применяется в технике, например, при тушении пожара для получения сильной и дальнобойной струи воды.

Гидродинамический напор

Гидродинамический напор H (м) — это энергетическая характе­ри­стика движущейся жидкости. Понятие гидродинамического напора в гидравлике имеет фундаментальное значение.

Гидродинамический напор H (рис. 9) определяется по формуле :

,

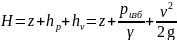где z — геометрический напор (высота), м;

h_p — пьезометрический напор (высота), м;

h_v = v²/2g — скоростной напор, м;

v — скорость потока, м/c;

g — ускорение свободного падения, м²/с.

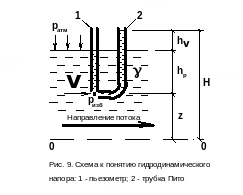
Гидродинамический напор, в отличие от гидростатического, скла­дывается не из двух, а из трёх составляющих, из которых дополни­тель­ная третья величина h_v отражает кинетическую энергию, то есть нали­чие дви­жения жидкости. Первые два члена z+h_p, также как и у гидро­ста­тического, представляют потенциальную энергию. Таким обра­зом, гидродинамический напор отражает полную энергию в конкретной то­чке потока жидкости. Отсчитывается напор от нулевой горизонтальной пло­скости О-О.

В лаборатории величина скоростного напора h_v может быть измерена с помощью пьезометра и трубки Пито по разности уровней жидкости в них (см. рис. 9). Трубка Пито отличается от пьезометра тем, что её нижняя часть, погружённая в жидкость, обращена против движения потока. Тем самым она от­кликается не только на давление столба жидкости (как пьезометр), но и на скоростное воздействие набегающего потока.

Практически же величина h_v определяется расчётом по значению ско­рости потока v.

2.4.1. Уравнение Бернулли для идеальной несжимаемой жидкости.

Если рассматривать установившееся течение жидкости, то в результате интегрирования уравнения Эйлера можно получить уравнение Бернулли для несжимаемой идеальной жидкости при течении без обмена механической энергией с внешней средой.

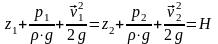
С энергетической точки зрения уравнение Бернулли представляет собой сумму удельной потенциальной энергии положения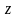 , удельной потенциальной энергии давления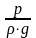 и удельной кинетической энергии жидкости .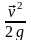

С напорной точки зрения:

- геометрический напор,

- пьезометрический напор,

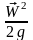- скоростной напор.

Сумма всех напоров Н представляет собой полный гидродинамический напор.

Напор измеряется в единицах длины.

Так как слогаемые уравнения Бернулли представляют собой удельную энергию, отнесённую к единичной силе, то:

2.4.2. Уравнение Бернулли для потока реальной (вязкой) жидкости .

При переходе от элементарной струйки идеальной жидкости к потоку реальной вязкой жидкости, имеющему конечные размеры и ограниченному стенками, необходимо учесть:

Во-первых, неравномерность распределения скоростей по сечению,

Во-вторых, потери энергии (напора) жидкости.

То и другое является следствием наличия сил трения между слоями вязкой жидкости.

Неравномерное распределение скоростей (см. рис.2.2) обусловлено скольжением одних слоев по другим, вследствие чего возникают касательные напряжения трения.

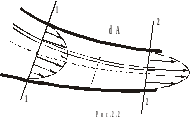
Во-первых, это требует затрат энергии.

Поэтому удельная энергия движущейся вязкой жидкости не остается постоянной, как в случае идеальной жидкости, а постепенно расходуется на преодоление сопротивлений и, следовательно, уменьшается вдоль потока.

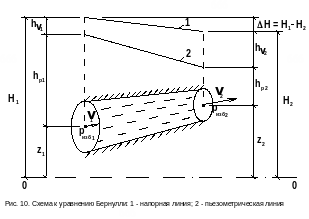
Рассмотрим поток жидкости, проходящий по трубопроводу переменно­го сечения (рис. 10). В первом сечении гидродинамический напор пусть ра­вен H₁. По ходу движения потока часть напора H₁ необратимо потеря­ется из-за проявления сил внутреннего трения жидкости и во втором сечении напор уменьшится до H₂ на величину потерь напора ΔH=Н₁-Н₂=h_п.

При наличии потерь:

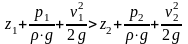
Или можно записать:

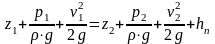
Во-вторых, неравномерность распределения скоростей влияет на величину кинетической энергии, что в уравнении Бернулли учитывается так называемым коэффициентом Кориолиса:

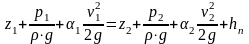
где

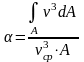- безразмерный коэффициент Кориолиса, учитывающий

неравномерность распределения скоростей.

Физический смысл коэффициента Кориолиса – это отношение действительной кинетической энергии потока в данном сечении к кинетической энергии того же потока и в том же сечении, но при равномерном распределении скоростей.

Для неравномерного распределения скоростей по сечению потока коэффициент Кориолиса всегда больше 1, при равномерном распределении скоростей коэффициент Кориолиса равен 1.

При использовании обозначений пьезометрического h_p и скоростного h_v напоров уравнение Бернулли можно записать и так:

z₁ + h_p1 + α·h_v1 = z₂ + h_p2 + α·h_v2 + h_п .

Энергетический смысл уравнения Бeрнулли заключается в том, что оно отражает закон сохранения энергии: сумма потенциальной z+h_p, кинетической v²/2g энергии и энергии потерь ΔH остаётся неизменной во всех точках потока.

Геометрический смысл уравнения Бeрнулли показан на рис. 10:

• сумма четырёх высот z, h_p, h_v, ΔH остаётся неизменной во всех точках потока.

Уравнение Бернулли применимо не только для жидкостей, но и для газов, при условии, что скорость газа 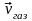значительно меньше скорости звука.