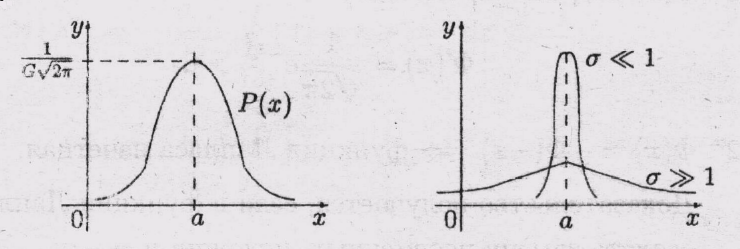Основные распределения в теории вероятностей (часть 3)
Дискретные с.в. |
p – вероятность появления события А в каждом из n независимых испытаний, q=1-p с.в. Х – число появлений события А в серии из n независимых испытаний, Х=0,1,2,…,m,…,n
P(X=m)=Pп(m)=
М(Х)=np;
D(X)=npq;
σ(X)= |
||||||||||||||
p – вероятность появления события А в каждом из n независимых испытаний, q=1-p (случай, когда n достаточно большое, а p – достаточно малое). Пусть a=np – параметр распределения Пуассона.
Х
0
1
2
…
m
…
Р
e-a
e-a/1!
e-a
a2/2!
…
e-a
am/m!
…
М(Х)=a;
D(Х)=a;
σ(Х)=
|
|||||||||||||||
С.в. X=m, имеющая геометрическое распределение, представляет собой число m испытаний, проведённых по схеме Бернулли, с вероятностью p наступления события в каждом испытании до первого положительного исхода, X=1,2,…,m,…., q=1-p P(X=m)=qm-1p. Закон распределения с.в.X:
|
|||||||||||||||
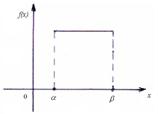
Абсолютно-непрерывные с.в. |
|
||||||||||||||
|
|||||||||||||||
Правило трёх
сигм:
|

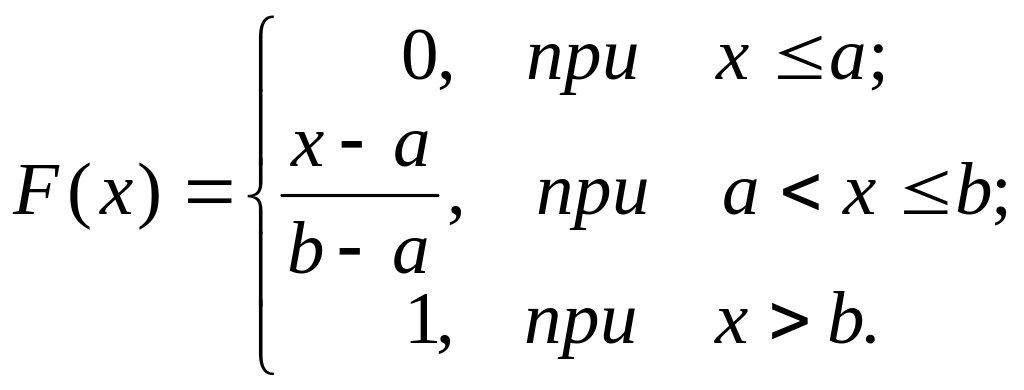

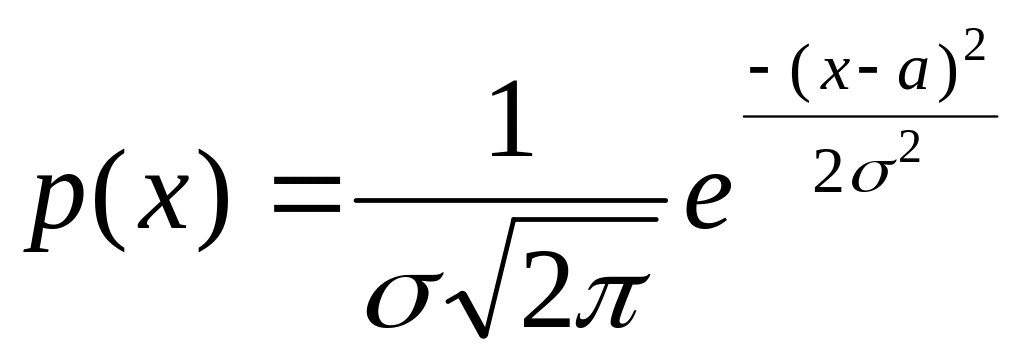 ;
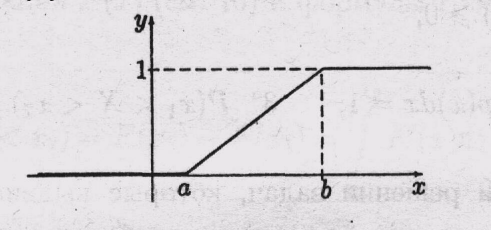
;